Yunan matematiğinin altın çağının en önemli isimlerinden biri olan Pergeli Apollonius, Arşimet ve Öklid ile birlikte anılmayı hak eden bir matematikçidir. Onun konikler üzerine yaptığı çalışmalar, yalnızca kendi döneminde değil, bilimin gelişiminde de kalıcı bir etki bırakmıştır.

Apollonios, MÖ 262 ile 190 yılları arasında yaşadığı tahmin edilen önemli bir Antik Yunan matematikçisidir. Günümüzde Antalya il sınırları içinde yer alan Pamfilya bölgesindeki Perge kentinde doğmuş, bir süre İskenderiye’de eğitim görmüş ve ardından İskenderiye okulunu örnek alan Pamfilya’daki Bergama’da öğretmenlik yapmıştır.
Apollonios’un dönemindeki diğer büyük matematikçiler arasında Öklid ve Arşimet yer alır. Özellikle Arşimet, Apollonios’tan 25 ila 40 yıl daha yaşlı olmasına rağmen, onun en önemli entelektüel rakiplerinden biri olarak görülür. Bu rekabet ortamı nedeniyle her iki matematikçi de benzer konulara yönelmiştir. Örneğin, her ikisi de büyük sayıların ifade biçimleri, astroloji ve konikler gibi alanlarda çalışmıştır.
Arşimet, konik kesitleri adlandırmak için bazı terimler kullanmıştı. Ancak Apollonios, bu fikirleri sistematikleştirerek bugün hâlâ kullandığımız elips, parabola ve hiperbol terimlerini literatüre kazandırmıştır.
Nasıl ki Öklid’in Elementler adlı eseri geometriye yön verdiyse, Apollonios’un Konikler adlı çalışması da konikler kuramına aynı derecede derinlik kazandırmıştır. Öyle ki, bazı kaynaklara göre Apollonios, konik eğrilerin özelliklerini o kadar ayrıntılı biçimde incelemiştir ki, kendisinden sonra gelen matematikçilere katkı yapacak pek az şey kalmıştır.
Apollonius ve Konikler
Apollonios, “Büyük Geometri Ustası” olarak anılır. Bu unvan, onun ve Öklid’in birçok çalışmasını bir araya getiren Pappos sayesinde günümüze ulaşır. Apollonios’un fikirlerini devrim niteliğinde kılan unsurlardan biri, tanımladığı konik eğrileri çizebilecek düzeyde bir geometrik aletin muhtemelen ancak yaklaşık bin yıl sonra geliştirilmiş olmasıdır. Yani, onun kavramsal düzeyde ulaştığı soyutluk, kendi döneminin teknik imkânlarının çok ötesindedir.

Daha da dikkat çekici olan, Apollonios’un matematiğe bu denli derin katkılar sunmasına rağmen, eserlerinin büyük bölümünün kaybolmuş olmasıdır. Başyapıtı sayılan Konikler adlı sekiz kitaplık seriden yalnızca yedisi günümüze ulaşır.
Bunlardan dördü orijinal Yunanca metinlerle, geri kalan üçü ise Arapça çeviriler yoluyla korunur. Bu durum, Apollonios’un etkisinin yalnızca Antik Yunan matematiğiyle sınırlı kalmayıp, İslam dünyası aracılığıyla Orta Çağ bilim geleneğine de aktarıldığını gösterir.
Konikler Nasıl Sınıflandırılır?
Konikler, bir koninin farklı düzlemlerle kesilmesiyle oluşan geometrik şekillerdir. Bu kesitler yedi farklı türde ortaya çıkar: tek bir nokta, tek bir doğru, iki doğru, parabol, elips, çember (elipsin özel bir durumu) ve hiperbol. Apollonios, bu yedi şeklin tamamının, farklı açılarla kesilen aynı türden bir koniden elde edilebileceğini göstermiştir.
Koninin tepe noktasından (verteks) geçen düzlemlerle oluşan kesitlere dejenere konikler denir. Bu sınıfa giren şekiller, tek bir nokta, tek bir doğru ve kesişen iki doğrudur. Bunlar, klasik anlamda birer eğri değil, koniklerin sınır durumlarıdır. Buna karşılık, parabol, elips ve hiperbol gibi eğri biçimli kesitler, dejenere olmayan koniklerdir.
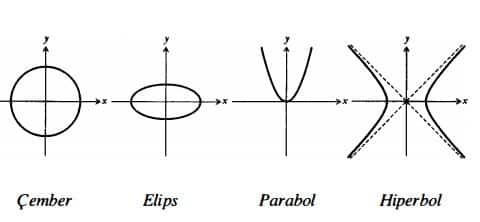
Dejenere olmayan konik eğriler, ortak bazı özellikler taşır. Bu özellikler, onları temsil eden standart denklemlerin oluşumuna temel oluşturur. Bu eğriler arasında fark yaratan temel unsur, eksantriklik (eccentricity) katsayısıdır. Her bir konik eğri — elips, parabol ve hiperbol — bir ya da iki odak noktası , bir doğrultman ve belirli bir eksantriklik değeriyle tanımlanır. Eksantriklik değeri, eğrinin türünü belirler:
- Elips için: 0 < e < 1
- Parabol için: e = 1
- Hiperbol için: e > 1
Apollonios, konik eğrilerin yalnızca geometrik şekiller olmadığını, aynı zamanda belirli matematiksel yasalarla tanımlanabileceğini göstermiştir. Koniklerin genel denklemi şu biçimdedir:
Ax² + Bxy + Cy² + Dx + Ey + F = 0. Burada A ve C katsayılarının aynı anda sıfır olmadığı varsayılırsa, bu denklem bazı özel formlara indirgenir.
- Ax² = 0
- Ax² + Cy² = 0
- Ax² + F = 0
- Ax² + Cy² + F = 0
Bu ifadelerden bazıları, dejener konikler olarak adlandırılan özel durumları temsil eder. Dejener konikler, klasik anlamda bir eğri oluşturmaz. Bir konik kesitin gerçek bir eğri olduğunu belirlemek için, denklemin diskriminant değeri incelenir. Bu diskriminant, δ = AC − B² şeklinde tanımlanır.
- Elips (δ < 0): Konik, elips formundadır. Örnek denklem: x² + y² = 1
- Hiperbol (δ > 0): Konik, hiperbol formundadır. Örnek denklem: x² − y² = 1
- Parabol (δ = 0): Konik, paraboldür. Örnek denklem: x² + By = 0
Apollonius’un Yeniden Keşfi
Bu sınıflandırma, Apollonios’un koniklere getirdiği sistematik yaklaşımın analitik temellerini oluşturur. Onun katkısı, yalnızca geometrik sezgiyle değil, cebirsel biçimde de konik eğrilerin doğasını anlamayı mümkün kılmıştır.

Apollonios, astronomi alanında da dikkat çekici katkılarda bulunmuştur. Aristoteles’in, gökcisimlerinin dairesel yörüngelerde hareket etmeleri gerektiği yönündeki görüşünü esas alarak, gezegenlerin zaman zaman geriye gidiyormuş gibi görünmesini bu anlayışla uyumlu hale getirmeyi başarmıştır.
Bu durumu, gezegenlerin ana yörüngeleri üzerinde dönen küçük çemberler tanımlayarak açıklar. Apollonios’un bu modeli, daha sonra Hipparkhos (MÖ 190–120) ve Claudius Ptolemaios (MS 100–180) tarafından geliştirilerek, yermerkezli evren anlayışının temel taşlarından biri hâline gelmiştir.
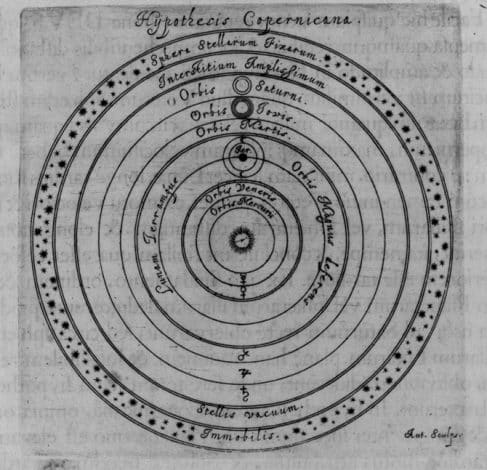
Nikolaus Kopernik bile, Güneş merkezli sistemini gözlemlerle uyumlu hâle getirmek için aynı fikri kullanmıştır. Ancak, Johannes Kepler’in gezegenlerin dairesel değil, eliptik yörüngelerde hareket ettiğini ortaya koymasıyla bu karmaşık sistemlerin gerekliliği ortadan kalkmıştır.
Apollonius’un çalışmaları olmasaydı, büyük olasılıkla Kepler’in gezegen hareketleri yasaları, Newton’un yerçekimi teorisi ve modern astronominin gelişimi mümkün olmazdı. Bilime yaptığı büyük katkılardan dolayı, Apollonios’un adı Ay üzerindeki bir kraterde yaşatılmaktadır.
Kaynaklar ve ileri okumalar:
- Apollonius of Perga; https://mathshistory.st-andrews.ac.uk/
- M., G. Apollonius of Perga: Treatise on Conic Sections. Nature 54, 314–315 (1896). https://doi.org/10.1038/054314a0
- Aslan Seyhan, Irem. (2022). A Historical Overview of Apollonius’ Conic Sections.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel