Bu yazıda, “cevabını bilseniz bile imkânsız gibi görünen” ünlü bir matematik bilmecesinden söz edeceğiz: 100 Mahkûm Problemi.
Olasılık teorisi ve kombinatorik alanlarında klasikleşmiş bu problem, 2003 yılından bu yana, şaşırtıcı derecede etkili ve zarif çözümü sayesinde daha da büyük ilgi görmeye başlamıştır.
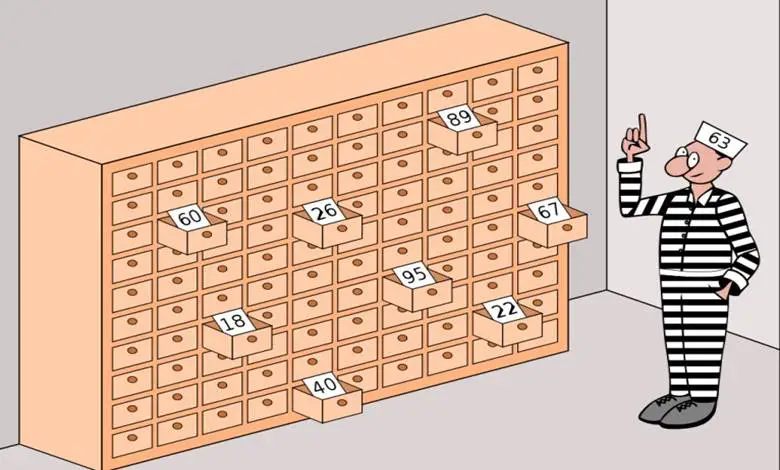
Problemin kurgusu şöyle: 100 mahkum var, her birinin üzerinde 1’den 100’e kadar bir numara yazıyor. Mahkumlar sırayla, üzerinde numaralar olan 100 kutunun bulunduğu bir odaya giriyor. Amaçları, kendi numaralarının yazılı olduğu kâğıdı bulmak. Her mahkum en fazla 50 kutu açabilir. Eğer hepsi kendi numarasını bulursa, topluca serbest kalacaklar.
Başlamadan önce bir kez toplanıp strateji belirleyebilirler. Ama ilk mahkum içeri girdikten sonra konuşmaları yasak. Soru şu: Mahkumlar nasıl bir strateji izleyerek kurtulma şanslarını en yükseğe çıkarır?
İlk bakışta, mahkumların iyi bir strateji geliştirebileceği pek gerçekçi görünmez. En olası senaryo, her mahkumun 50 çekmeceyi rastgele seçmesidir. Bu durumda, her mahkumun kendi numarasını bulma olasılığı %50 olur. İki mahkum için her birinin başarı şansı %50 olduğundan, ikisi de başarılı olma ihtimali 0.5 × 0.5 = 0.25 yani dörtte bir olur.
100 mahkum için bu olasılık şöyle olur: 0.5100 ≈ 0.000000000000000000000000000008 Bu rakamın ne kadar küçük olduğunu görmek kolay. Bu nedenle mahkumların affedilme şansı yokmuş gibi görünür.
Ama aslında öyle değildir. Gerçekten de başarı şansını %30’un üzerine çıkaran bir strateji vardır! Yaratıcılık ve matematik bazen şaşırtıcı çözümler sunar. Ana fikir, mahkumların açtıkları çekmecelerden elde ettikleri bilgiyi bir sonraki adımda hangi çekmeceyi açacaklarına karar verirken kullanmalarıdır.
100 mahkum problemi nasıl çözülür?
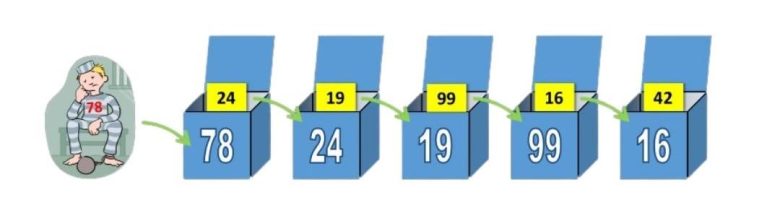
Önce çözümün ne olduğunu, ardından neden işe yaradığını açıklayalım. Strateji son derece basittir. Mahkum, önce kendi numarasına karşılık gelen kutuyu açar. Eğer kendi biletini bulursa başarılı olur. Bulamazsa, açtığı kutuda çıkan numaraya karşılık gelen kutuyu bir sonraki adımda açar. Bu işlem, her seferinde bir sonraki numaraya yönelerek zincirleme şekilde devam eder.
Örneğin numarası 30 olan mahkum önce 30 numaralı çekmeceyi açar. Eğer içinde 30 numarası varsa iş tamamdır. Ama başka bir numara bulursa, o numaraya karşılık gelen çekmeceyi açar. Bu işlemi ya kendi numarasını bulana kadar ya da 50 çekmece açana kadar tekrarlar.
Bir noktada 30’u bulursa başarılı olur ve kurtulma şansı olur. Ama 50 çekmece açmasına rağmen bulamazsa, herkes idama mahkûm olur. İddiamız şu: Eğer mahkumlar belli bir stratejiyi izlerse, affedilme olasılıkları %31’in üzerine çıkar!
İlk bakışta bu strateji, kutuları tamamen rastgele seçmekten farklı görünmeyecektir. (ve tek bir mahkum için gerçekten fark yaratmaz). Ancak tüm mahkumlar aynı biçimde davranacağı için sonuç üzerinde çok büyük bir etkisi olur.
Her kutuda bir tane bilet bulunur ve bu biletler birbirinden farklıdır. Bu durum, bir biletin ya doğru kutuda olduğu ya da başka bir kutuya işaret ettiği anlamına gelir. Biletler benzersiz olduğundan, her kutuya yalnızca bir bilet yönlendirme yapar ve her kutuya ulaşmanın yalnızca bir yolu vardır. Düşünüldüğünde, kutular dairesel zincirler oluşturur. Her kutuda yalnızca bir çıkış ve bir giriş yönlendirmesi olduğundan, bir kutu yalnızca tek bir zincirin parçası olacaktır.
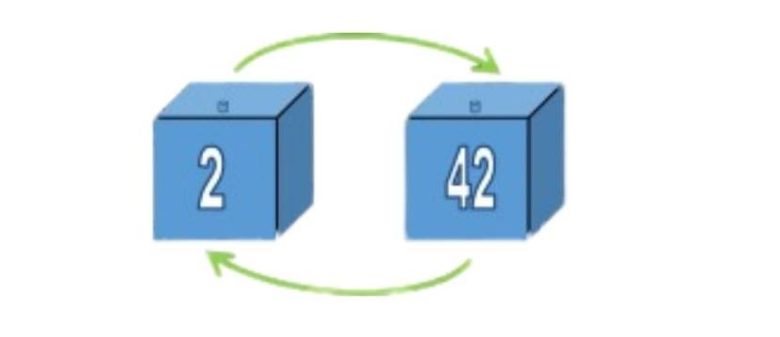
Bir kutu kendi biletini içermiyorsa, mutlaka bir zincirin parçasıdır. Bazı zincirler yalnızca iki kutu uzunluğunda olabilirken, bazıları çok daha uzun olabilir.
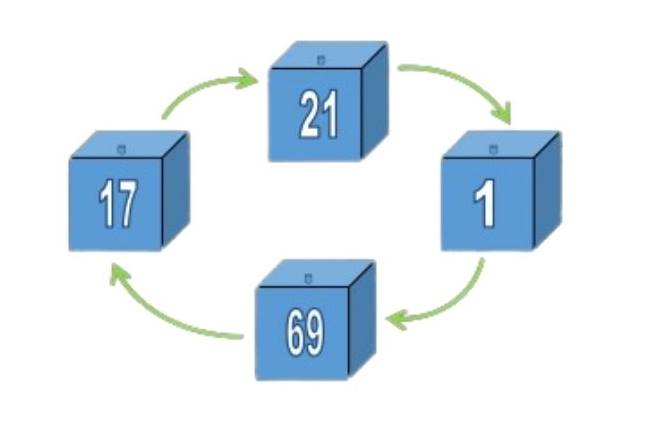
100 mahkum problemi ilginç bir ilişkiyi ortaya çıkarır
Herkesin başarılı olabilmesi için en uzun zincirin uzunluğu 50 kutudan kısa olmalıdır. Eğer bir zincir 50 kutudan uzunsa, o zincirdeki mahkumlar biletlerini bulamaz ve bu da tüm mahkumların başarısız olmasına yol açar.
Bunu bir an düşünün. Örneğin zincir uzunluğu 51 ise, mahkum aramaya kendi numarasının kutusundan başlayarak her adımda zinciri takip eder ve biletini zincirin son kutusunda bulur. Ancak 51. kutuya ulaşmak için 51 adım gerekir ki bu mümkün değildir çünkü yalnızca 50 kutu açma hakkı vardır. Ayrıca, 51 uzunluğunda bir zincir oluşursa geriye sadece 49 kutu kalır. Bu nedenle 50’den uzun ikinci bir zincir olamaz.
Mahkum, kendi numarasına karşılık gelen kutudan başladığı için doğrudan kendi biletinin bulunduğu zincire dahil olur. Bu zinciri adım adım takip ederek eninde sonunda kendi biletine ulaşması garanti olur. Asıl mesele şu: Bu zincir 50’den kısa mı? Eğer zincir 50’den uzun ise o mahkum biletini bulamaz.
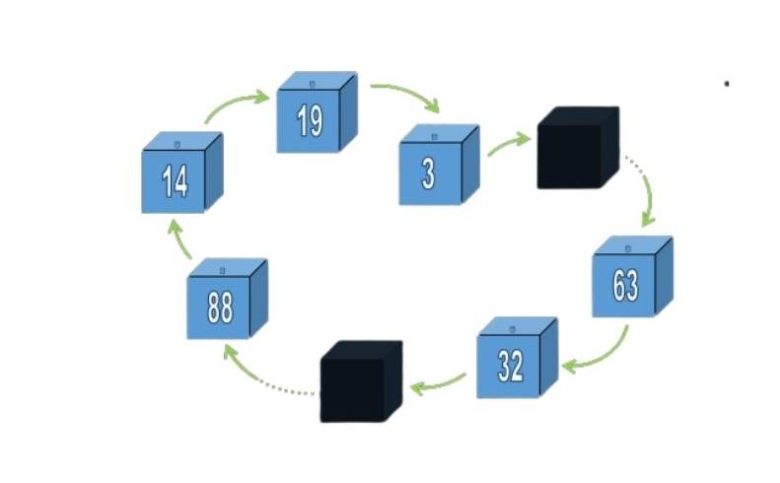
Başarı için maksimum zincir uzunluğunun 50 veya daha kısa olması gerektiğini ve 50’den uzun yalnızca bir zincir oluşabileceğini kabul edince, başarı olasılığını şöyle ifade edebiliriz:
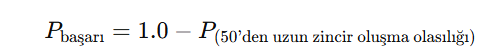
Öncelikle, 50’den uzun zincirlerin oluşma olasılığını bulmamız gerekiyor. Diyelim ki bir zincirin uzunluğu l. Hangi kutular zinciri oluşturacak? 100 kutudan l tanesini seçmemiz gerekiyor. Bunu yapmanın yolu:
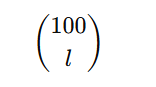
Zincir oluşturacak şekilde bu biletleri sıralamanın yolu (l−1)! olur. Geri kalan 100−l biletin ise nasıl yerleşeceği önemli değil (çünkü bunlar 50’den uzun bir döngü oluşturamaz). Bu geri kalan biletler (100−l)!şekilde yerleşebilir. Hepsini birleştirince aşağıdaki sonucu elde ederiz.
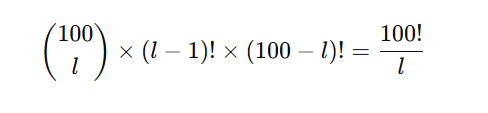
Sonuç olarak:
Toplamda tüm yerleşimlerin sayısı 100! Dolayısıyla, istediğimiz (tam l uzunluğunda zincir içeren) yerleşimlerin tüm olasılıklara oranı:
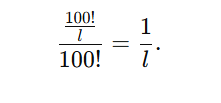
Başka bir deyişle, bir zincirin uzunluğu lll olduğunda, bunun oluşma olasılığı 1/l’dir. Bu sonuç çok ilginçtir çünkü olasılık, kutu sayısından tamamen bağımsızdır; sadece zincirin uzunluğuna bağlıdır. Bildiğimiz gibi, 50’den uzun yalnızca bir zincir oluşabilir (çünkü toplamda 100 kutu var ve bir zincir 51 kutu uzunluğunda olursa diğer zincirler en fazla 49 kutu olabilir). Bu yüzden, başarı olasılığı şöyle ifade edilir:
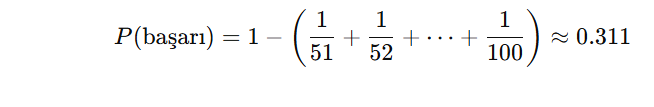
Bu strateji sayesinde mahkumların topluca kurtulma şansı yaklaşık %31’dir. Aynı bilmeceyi bir de şöyle düşünelim: Bu kez bir casus var. Casus, önceden odaya gizlice girip tüm biletlerin hangi kutuda olduğunu görebiliyor. Ayrıca (isterse) sadece iki biletin yerini değiştirebiliyor. Ancak yaptığı bu değişikliği mahkumlara söyleyemiyor. Peki şimdi ne olacak?
Daha önce öğrendiğimiz gibi, mahkumların başarısız olmasının tek sebebi 50’den uzun bir zincir oluşmasıydı. Casus yerleşimi incelediğinde böyle bir uzun zincir görürse, bu zincirin içindeki iki kutunun içeriğini değiştirerek zinciri iki daha kısa zincire bölebilir. Böylece tüm zincirler 50 veya daha kısa olur ve herkes biletini 50 adımda bulabilir.
Bu durumda mahkumlar önceden belirledikleri aynı zincir takip stratejisini uygular ve başarı garanti hale gelir.
Kaynaklar ve ileri okumalar
- The 100 prisoners escape puzzle. yayınlanma tarihi: 25 Eylül 2024. Kaynak site: The Network page. Bağlantı: The 100 prisoners escape puzzle
- The Riddle That Seems Impossible Even if You Know the Answer. Yayınlanma tarihi: 1 Temmuz 2022. Kaynak site: Real Clear Science. Bağlantı: The Riddle That Seems Impossible Even if You Know the Answer
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel