Benford Yasası: Bu Sıradışı Sayı Deseni Neden Her Yerde Karşımıza Çıkıyor?

Dünyayla aramızda bir bağ kuran ve onu bambaşka bir bakış açısıyla görmemizi sağlayan bazı şaşırtıcı matematiksel ilişkiler vardır. Bu bağlantılardan biri de Benford Yasası’dır.

Şimdi hemen etrafınıza bakın ve üzerinde bol miktarda sayı bulunan bir şey bulun. Bu bir gazete olabilir, gelir-giderlerinizi yazdığınız bir defter ya da sayılarla dolu herhangi bir belge. Ardından, seçtiğiniz verideki sayıları incelemeye başlayın.

Yapmanız gereken tek şey, sayıların ilk basamağına odaklanmak. Sıfırla başlayanları dikkate almayın. Şimdi, kaç sayının 1 ile, kaçının 2 ile, kaçının 3 ile başladığını sayın ve sonuçları bir yere not edin. Peki ne fark ettiniz?

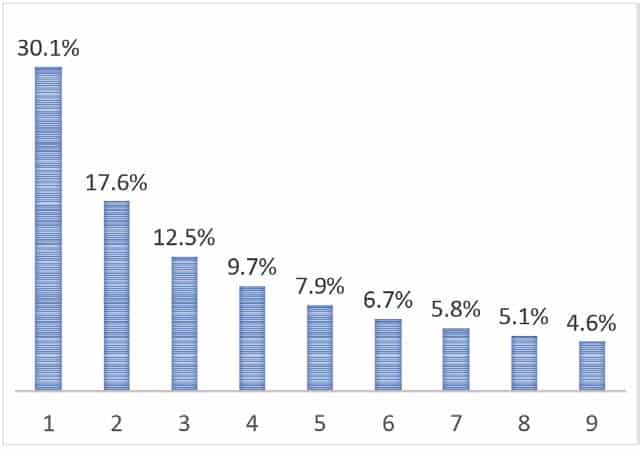
İlk bakışta, her rakamın eşit oranda görülmesi gerektiğini düşünebilirsiniz. Oysa ilk basamağın 1 olma olasılığı yaklaşık yüzde 30’dur. İlk basamak olarak 2 rakamı yaklaşık yüzde 17.6, 3 rakamı yüzde 12.5 oranında karşımıza çıkar. 9 rakamının ilk basamakta görünme olasılığı ise yalnızca yüzde 4.6’dır.

Bu durum size yalnızca basit bir gözlem gibi gelecektir. Ancak Benford Yasası, şimdiye dek insanları hapse göndermekten büyük ölçekli dolandırıcılık vakalarını ortaya çıkarmaya kadar pek çok ciddi olayda kullanılmıştır.

Benford Yasası Nedir?

Bu sıra dışı olgunun kökeni, 1881’de American Journal of Mathematics’te astronom Simon Newcomb’un yayımladığı kısa bir notta görülür. Newcomb, hesaplamalarda kullanılan logaritma tablolarının bazı sayfalarının diğerlerinden daha fazla yıprandığını fark etti. Özellikle 1 ile başlayan sayıların geçtiği sayfalar çok daha sık kullanılmıştı. Ancak 9 ile başlayan sayıların bulunduğu sayfalar ise neredeyse hiç yıpranmamıştı.

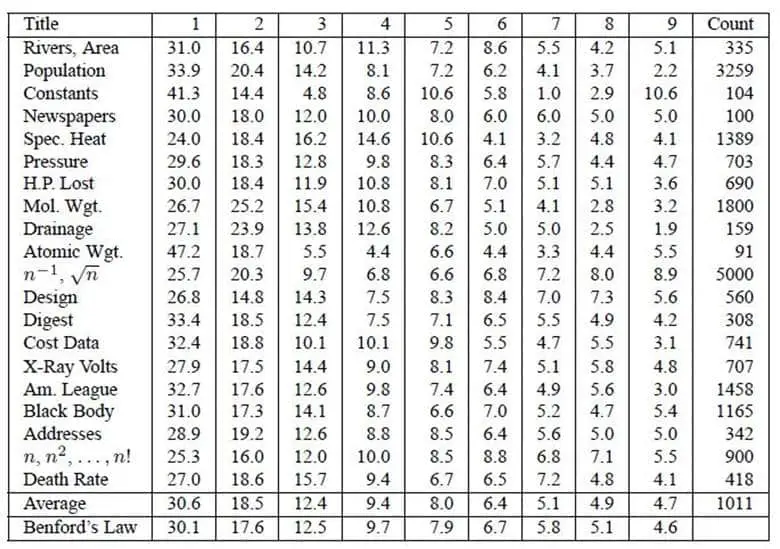
Bu dağılıma sağlam bir deneysel temel sunan kişi ise fizikçi Frank Benford oldu. Benford, 1938’de yayımladığı “The Law of Anomalous Numbers” adlı makalesinde beyzbol istatistiklerinden nehir alanlarına, dergi yazılarındaki sayılara kadar uzanan 20.229 farklı veri kümesini inceledi. Bu verilerin yaklaşık yüzde 30’unun 1 ile başladığını doğruladı.

Benford, bir sayının n rakamıyla başlama olasılığının 10 tabanında log(n + 1) − log(n) ifadesine eşit olduğunu gösterdi. Böylece bir sayının örneğin 2 ile başlama olasılığı log10(2 + 1) − log10(2) = 0.1761, yani yüzde 17.61 olur.

Benford Yasası Nasıl Çalışıyor?

Benford Yasası’nın geçerli olabilmesi için bazı koşulların sağlanması gerekir. Bu koşullardan biri, sayıların aynı türden olmasıdır. Sayıların yapay sınırlarla belirlenmemesi de önemlidir. Ev numaraları ya da bir süpermarketteki şarapların fiyat aralıkları bu yüzden Benford dağılımına uymaz.

Benford Yasası evrensel bir yasa değildir; yalnızca uygun veri kümelerinde, yani insan yapımı sınırlamalardan uzak, doğal şekilde oluşan verilerde ortaya çıkar.

Bunu anlamanın en iyi yollarından biri, geometrik bir büyüme örneğine bakmaktır. Diyelim ki bir hisse senedi her yıl yüzde 4 değer kazanıyor. 1 dolar ile başlarsak bir yıl sonra 1.04 dolarımız olur. İki yıl sonra 1.0816 dolar olur ve bu büyüme sürerek yaklaşık 17.67 yıl sonra 2 dolara ulaşır. 10 dolara erişmek ise yaklaşık 58.71 yıl alır.

Büyüme her adımda aynı oranda gerçekleştiğinden, sayılar 1’den 2’ye geçerken 9’dan 10’a geçerken olduğundan daha uzun süre 1 ile başlayan aralıkta kalır. Aralık genişliği aynı olmasına rağmen, 9 civarındaki artış miktarı daha büyük olduğu için geçiş daha hızlı olur. Bu yüzden sayılar, 1 ile başlayan değerlerde daha fazla “zaman” geçirir.

Matematiksel olarak ifade edersek: t anında elimizde 1.04ᵗ dolar bulunur. Bu değer 2 olduğunda t log(1.04) = log(2) olur ve t₂ = log(2) / log(1.04) çıkar. 10 dolara ulaştığımız zaman ise t₁₀ = log(10) / log(1.04) olur ve bu yaklaşık 58.71 yıldır.

Böylece ilk basamağı 1 olan değerlerde geçirdiğimiz sürenin toplam süreye oranı t₂ / t₁₀ = log(2) / log(10) olur. Logaritmalar 10 tabanında olduğu için bu oran log(2)’ye eşittir.

Aynı mantık diğer ilk basamak rakamları için de geçerlidir. Bu nedenle Benford Yasası, geometrik büyüme süreçlerinde kendiliğinden ortaya çıkar.

Sayılar Yardımı İle Dolandırıcılık Tespiti

Benford Yasası, doğal ya da insan kaynaklı verilerin çoğunu çıplak gözle fark edemeyeceğimiz kadar ince ama matematiksel olarak açık seçik kalıpların yönettiğini gösterir. Verilerin küçük ilk basamaklara doğru eğilim göstermesi, evrendeki birçok olgunun çarpan etkisiyle büyümesinin bir sonucudur. Bu durum ekonomiden jeolojiye kadar pek çok sürecin yapısında yankı bulur.

Bir kişi vergi beyannamelerini tahrif etmeye kalkıştığında, genellikle bazı verileri değiştirmesi ve yeni veriler eklemesi gerekir. Oysa Benford Yasası, doğal yollarla oluşan sayı kümelerinde geçerli olan istatistiksel bir düzen ortaya koyar. Bu nedenle, bir düzenbazın sahte veriler üretirken bu doğal düzeni taklit etmesi çoğu zaman mümkün değildir.

İşte bu tür küçük keşiflerin ardından, Benford Yasası, birçok muhasebeci için dolandırıcılık tespitinde kullanılan resmi araçlardan biri hâline geldi. Örneğin yasa, 2001 yılında Yunanistan’ın ekonomik verilerinin doğruluğunu analiz etmek amacıyla kullanıldı. Sonuçta, ülkenin Avrupa Birliği’ne katılmak için verilerini manipüle ettiği ortaya çıktı.

Günümüzde ise bu yasa, yalnızca finansal verilerde değil, sahte haber ve dijital görüntüleri tespit etmede de kullanılmaktadır. Dijital fotoğraflar da temelde sayısal verilerden oluşur. Bu görüntüler üzerinde oynama yapıldığında, içerdiği sayıların Benford Yasası’na olan uyumu bozulur. Aslında bunun ardındaki mantık oldukça açıktır. Doğal süreçler, küçük rakamların daha sık göründüğü bir dağılım üretir. Ancak manipülasyon içeren yapay yöntemler bu dağılımı sağlayamaz.

Sonuç Olarak

Yaklaşık 150 yıl önce, bir adamın bir kütüphane kitabında yaptığı basit bir gözlem, günümüzde hâlâ matematikçileri şaşırtmaya devam ediyor. Yaşamlarımızdaki kaosta ve tesadüflerde kimi durumlarda matematiksel bir düzen var gibi gözüküyor.

---

Kaynaklar ve ileri okumalar:

• How a simple observation from the. 1800s about patterns in big data sets can fight fraud. Yayınlanma tarihi: 10 Kasım 2015; Kaynak site: Conversation. Bağlantı https://doi.org/10.64628/AAI.xayafd6ss
• Looking out for number one; Yayınlanma tarihi: 1 Eylül 1999; Bağlantı: https://plus.maths.org/content/looking-out-number-one
• Cerasa A. Testing for Benford’s Law in very small samples: Simulation study and a new test proposal. PLoS One. 2022 Jul 22;17(7):e0271969. doi: 10.1371/journal.pone.0271969. PMID: 35867697; PMCID: PMC9307211.

Matematiksel