Bir matematikçi değilseniz Voronoi diyagramları adını ilk defa duyuyor olmanız olasıdır. Ancak farkında olmasınız da hemen her gün bu şekiller ile yüzleşirsiniz. Bu şekillerin bir örneğini aşağıda, yusufçuğun kanatlarında görebilirsiniz.

Adını matematikçi Gregory Voronoi’den ( 1868- 1908) alan Voronoi diyagramları belirlenmiş bir bölge içinde, noktalardan ya da nesnelerden oluşan bir kümenin birbirlerine göre yakınlık bilgilerini gösterir. Voronoi diyagramları günümüzde başta bilim ve teknoloji olmak üzere görsel sanatlar da dahil pek çok alanda pratik ve teorik uygulamalara sahiptir. Şimdi gelin bu şekiller hakkında biraz daha bilgi edinelim.

Voronoi diyagramları her türlü alanda faydalıdır. Örneğin, ormanların büyüme modellerini incelemek veya robotların bir dizi engel boyunca net rotalar bulmasına yardımcı olmak için kullanılabilirler. Bir hizmet alanındaki (yani bir hücredeki) kahve içenler, hastalar veya öğrenciler kendi kafelerine, hastanelerine veya okullarına (yani kendi hücrelerinin bulunduğu yere) diğerlerinden daha yakın yaşamalıdır. İşte bu nedenle şehir planlamacıların tümü Voronoi diyagramlarını dikkate alır.
Voronoi Diyagramları Nedir?
Bir çok hastanesi olan bir şehir düşünün. Aniden rahatsızlanan birinin en yakın hastaneye gitmesini istersiniz. Bu durumda bir haritaya ihtiyacınız var. Ancak bu haritanın her hastanenin hizmet alanını göstermesi gerekiyor. Peki böyle bir haritayı nasıl yapılabiliriz? İşte bu tip durumlar da işin içine Voronoi diyagramları karışır.
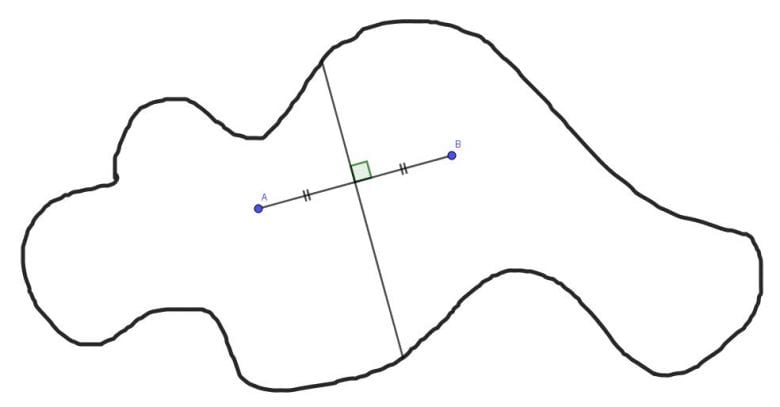
A ve B adlı iki hastanenin olduğu bir harita üzerinde A ve B hastanelerini birbirine bağlayan bir doğru parçası çizelim. Sonrasında bu doğru parçasının orta dikmesini çizelim. Bu çizilen doğru şehri iki bölgeye ayıracaktır. A hastanesinin bulunduğu bölgedeki her insan A hastanesine B hastanesine göre daha yakın olacaktır.
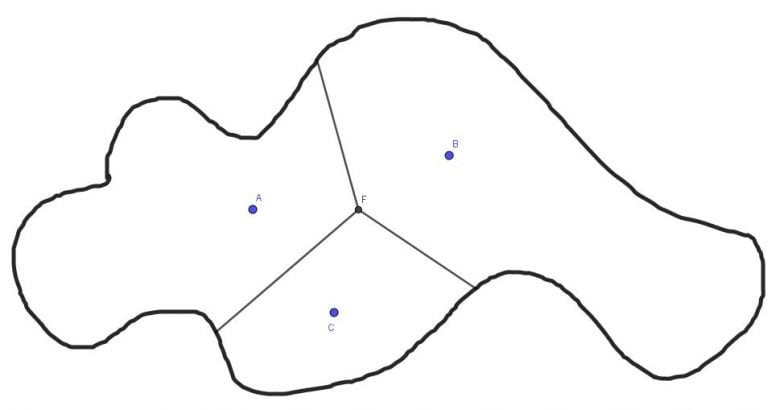
Şimdi 3. hastane olan C hastanesini de şehir haritasına ekleyelim. Ve aynı şart yine sağlansın. 3 hastane 3 bölge. Her bir bölgenin sakinleri yaşadıkları bölgenin hastanesine diğer hastanelere göre daha yakın olacaktır. Yukarıda yapılan işlemleri tekrarlamak suretiyle A ile C hastanelerini birleştiren doğru parçasının ve B ile C hastanelerini birleştiren doğru parçasının orta dikmelerini çizelim. Bunların hepsi ortak bir F noktasında kesişecektir. Bu F noktası ile A, C hastaneleri ile B, C hastanelerini birleştiren doğru parçası dışında kalan kısımların silinmesiyle harita aşağıdaki şekli alacaktır.
Şehir haritasındaki tüm hastaneler bitene kadar bu şekilde devam edilerek oluşturulan bölgelerin sakinleri kendi hastanelerine diğer hastanelerden daha yakın olacaktır. Böylelikle ihtiyacımız olan haritayı elde etmiş oluruz.
Bu hastane örneğini bir nedenden ötürü seçtik. ohn Snow (1813-1858) genellikle “Epidemiyolojinin Babası” olarak anılır. Bir felaketle ilgili araştırması epidemiyologlar arasında klasik kabul edilir. Bu olay da Voronoi diagramlarının kullanım alanlarına dair güzel bir örnek olarak kitaplarda yer alır.
Kolera Salgını ve John Snow’un Haritalandırma Çalışması
On dokuzuncu yüzyılın en korkunç hastalığı olan kolera olarak kabul edilmektedir. Kolera Hindistan’da binlerce yıldır insanlara eziyet etmesine rağmen, nedenini ortaya çıkarmak için önemli adımlar ancak Avrupa’ya ulaştığında atıldı. Günümüzde koleraya Vibrio cholerae adlı bir bakterinin neden olduğunu artık biliyoruz. Bu bakteri insanlara enfekte su içtiklerinde ya da az pişmiş veya çiğ kabuklu deniz ürünleri tükettiklerinde bulaşabilir. Ancak bir zamanlar İngiltere’de yaşayanlar elbette bu bilgiye sahip değildi.

O zamanlar salgınların kökenleri ve nasıl yayıldıkları üzerine tartışmalar çok yaygındı. 1845 ve 1856 yılları arasında Londra’da yalnızca kolera üzerine 700’den fazla çalışma yayımlanmıştı. En yaygın kabul gören, hastalıkların ceset veya kanalizasyon gibi kirli maddelerin yaydığı kötü havadan kaynaklandığını iddia ediyordu. Ancak eter ve kloroform gibi anesteziklerin kullanımını savunmasıyla tanınan doktor John Snow’un başka bir fikri vardı.
1849’da, Koleranın Bulaşma Tarzı Üzerine adlı eserini yayımladı. Karşılaştığı sayısız vakaya dair gözlemlerine dayanarak, koleranın suyla bulaşan bir hastalık olduğuna ikna olmuştu. Ancak meslektaşlarını da ikna etmesi gerekiyordu.
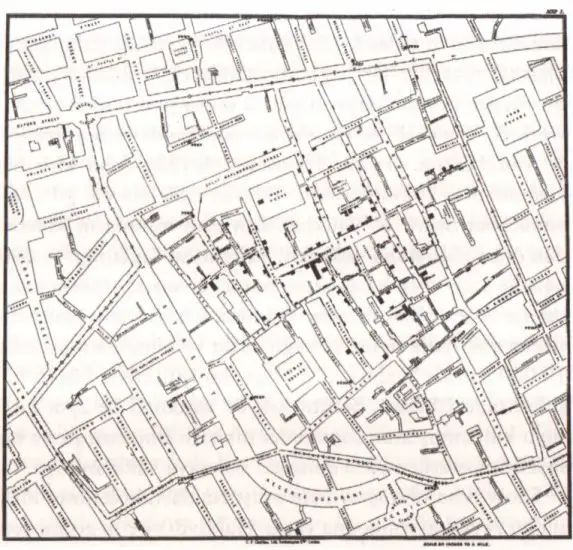
Snow ilk iş olarak Londra’da birisinin hastalıktan öldüğü tüm yerlerin ayrıntılı bir haritasını çıkardı ve ölen her hastayı siyah bir kareyle işaretledi. Snow, ölenlerin hepsinin Londra’nın aynı bölgesinde, Broad Street civarında bulunduğunu fark etti. Broad Street’teki su tulumbasının kolera ile enfekte olduğunu
doğru tahmin etti çünkü buradaki suyu kullanan herkes hastalanmıştı. Hastalıktan sadece kendi su tulumbaları olan yerel bira fabrikası ve yoksullar yurdu kurtulmuştu.
Snow, bulgularını yerel yetkililere sundu. Sonuçta pompa kaldırıldı ve kolera salgını sona erdi. Snow’un kolera’nın suyla taşındığına dair matematik yardımı ile ortaya koyduğu kanıt, hastalıkları anlamak için matematiğin kullanımının ilk örneğidir.
Voronoi Diyagramları Sadece İki Boyutlu Olmak Zorunda Değildir
Bir Voronoi diyagramı üç boyutlu olarak da karşımıza çıkar. Nerede sorusunun en basit cevabı vücudunuz olacaktır. Cildimiz, bağırsaklarımız, kan damarlarımız ve daha pek çek yer skutoid şekilli epitel hücreleri ile doludur. Bu hücrelerin dizilimi de üç boyutlu bir Voronoi diyagramı örneğidir.
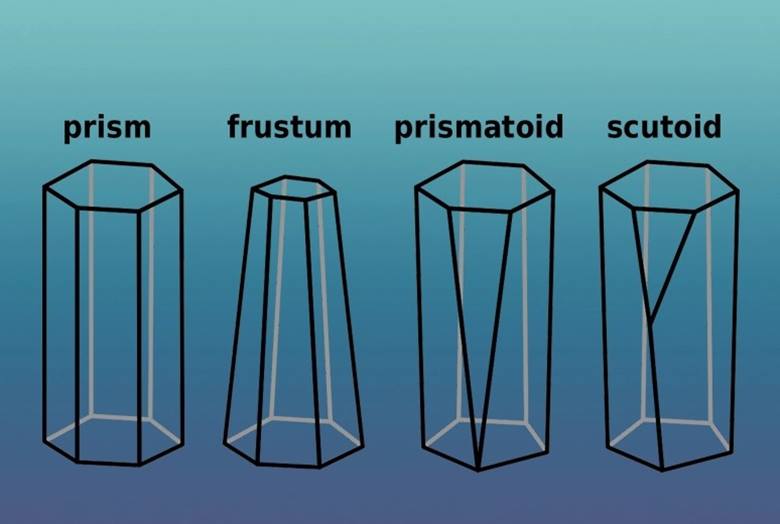
Epitel hücrelerin bu yapıların oluşmasında temel bir işlevi vardır. Epitel hücreler sıkı bir şekilde istiflenerek derimizin, kan damarlarının ve organların dış tabakalarını oluşturur. Bazı epitel hücreler skutoid biçiminde olmaları sayesinde kıvrımlı doku bölgelerinde sıkı bir şekilde istiflenebilir. Bu hücrelerin istiflenmesi ise Voronoi diyagramları biçiminde olur. Sonuç olarak gördüğünüz gibi farkında olmadan herkes Voronoi diyagramlarını kullanır. Kullanmasa bile vücudu onun için kullanmaktadır.
Kaynaklar ve ileri okumalar
- Maths in a minute: Voronoi diagrams; Yayınlanma tarihi: 30 Mart 2020. Kaynak site: Plus maths. Bağlantı: https://plus.maths.org/
- New Geometric Shape Discovered as Efficient Cell Storage in Nature; Yayınlanma tarihi: 31 Temmuz 2018. Kaynak site: Popular Science. Bağlantı: New Geometric Shape Discovered as Efficient Cell Storage in Nature
- Voronoi Tessellations and Scutoids Are Everywhere. Yayınlanma tarihi: 22 Ocak 2019; Bağlantı: Voronoi Tessellations and Scutoids Are Everywhere
- Gómez-Gálvez, P., Vicente-Munuera, P., Tagua, A. et al. Scutoids are a geometrical solution to three-dimensional packing of epithelia. Nat Commun 9, 2960 (2018). https://doi.org/10.1038/s41467-018-05376-1
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel