İnsanlık, var olduğundan beri uzayı düzenli bir biçimde temsil etmenin yollarını aradı. Antik çağlardan bu yana basit çizimler ve diyagramlar bu ihtiyaca kısmen yanıt verdi. Ancak bu çabalar, 18. yüzyılda Gaspard Monge’un çalışmaları ve tasarı geometri (descriptive geometry) ile ilk kez matematiksel kesinlik ve evrensellik kazandı.
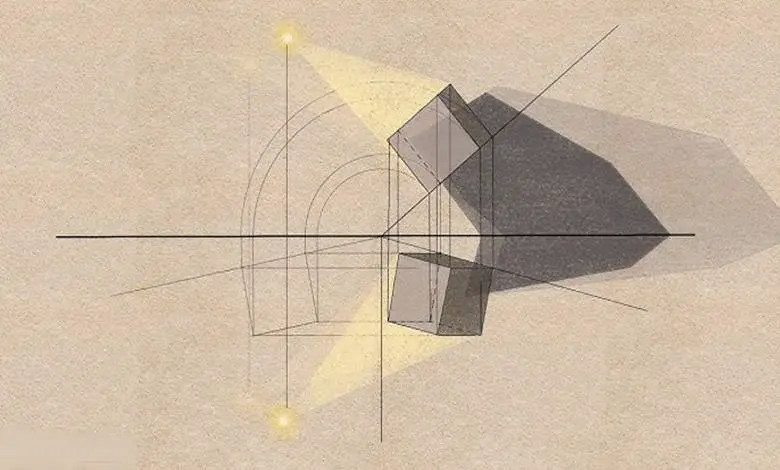
Uzayda bir nokta hayal edin. Uzay homojendir; her yerde aynı yapıdadır, ne kıvrımı ne de farklı bir özelliği vardır. Bu nedenle bu noktanın boyu, eni ya da derinliği yoktur; yalnızca küçük bir işarettir.
Şimdi bu noktanın yavaşça hareket ettiğini düşünün. Hareket ederken geride bir iz bırakır. Düz bir çizgi boyunca ilerlediğinde bu iz, bir doğru oluşturur. Şimdi bu doğrunun sabit kaldığını ve onun üzerinden dik yönde başka bir doğrunun geçtiğini düşünün. Bu ikinci doğru da hareket etmeye başladığında geride bir iz bırakacaktır. Sonucunda da ortaya düz bir yüzey, yani bir düzlem çıkacaktır.
Tasarı Geometri Nedir?
Uzaydaki her şeyi, hareket eden öğelerin geride bıraktığı izlerle tanımlamak fikri, Fransız matematikçi Gaspard Monge’un (1746–1818) geliştirdiği bir tekniğin temelini oluşturdu. Monge bu yönteme tasarı geometri adını verdi. Bu yaklaşımı öyle ustaca geliştirdi ki, uzayın tamamını bu hareketlerin ürünü olarak düşünmeyi mümkün kıldı.

Bu teknik, geometri kavramını ve öğretim yöntemlerini adeta yeniden tanımladı. Artık bir küpü sabit bir nesne olarak görmek yerine, birbirine dik doğruların hareketiyle oluşan üç boyutlu bir şekil olarak hayal etmek mümkündü.
Monge, uzayla ilgilendiği için koordinat geometrisine benzer bir sistem kullandı. Yeni bir düzlemi çizmek için, o düzlemin bu iki düzlemi nasıl kestiğini hayal etti. Kesişim çizgileri düzlemin izini belirliyordu. Artık nesneleri bu yansıtma düzlemleri üzerine, farklı açılardan yansıtmak mümkündü. Düzlemler birbirine katlandığında aralarındaki kesişim çizgisi, yönlendirme hattı olarak kullanılırdı.
Başlangıçta soyut bir düşünce egzersizi gibi görünen bu yöntem, zamanla teknik çizimlerin evrensel standardı hâline geldi. Monge, bu yeni geometriyi “üç boyutlu nesneleri iki boyutlu çizimlerle tam doğrulukla temsil etme sanatı” olarak tanımladı. Özellikle, bir nesnenin dikey ve yatay izdüşümlerini tek bir kâğıtta göstererek, bu çizimler üzerinden açı, kesişim ve uzunluk gibi geometrik özellikler hesaplanabiliyordu.
Bu teknik, binaların ve mühendislik tasarımlarının doğru biçimde inşa edilmesi için temel bir araç oldu. Günümüzde bu yöntem, “ortografik izdüşüm” (orthographic projection) adıyla kullanılmaktadır.
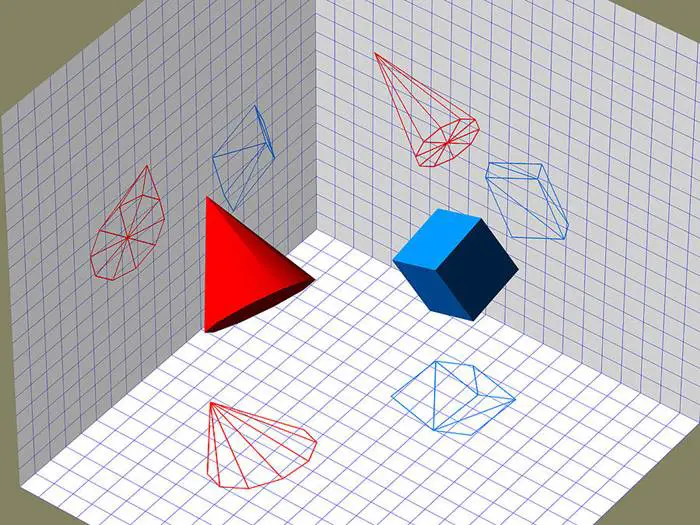
Eğer nesneleri çizdiğimiz iki düzlemi bir tür koordinat sistemi olarak kabul edersek, bu düzlemlerde oluşturulan şekilleri cebirsel tanımlarıyla da ilişkilendirebiliriz. Monge’un geliştirdiği bu sistem, o dönemde bilinen birçok yöntemi birleştiriyordu. Bu da onun daha sonra “diferansiyel geometrinin babası” olarak anılmasına yol açtı.
Diferansiyel geometri, cebir ve analizi bir arada kullanan yeni bir matematik dalıydı. Bu alan, özellikle düzgün yüzeylerin özelliklerini inceliyordu. Aynı dönemde çalışan başka matematikçiler de benzer yöntemler kullanmaya başlamıştı, ancak yalnızca Monge, diferansiyel geometriyi tasarı geometriyle birleştirmişti.
Gaspard Monge Tasarı Geometriyi Nasıl Buldu?
Monge’un bu iki yaklaşım arasındaki bağı fark etmesi, henüz on sekiz yaşındayken gerçekleşti. O yaşta Fransa’nın kuzeyinde yeni kurulan École Royale du Génie adlı askerî okulda çizer olarak çalışmaya başlamıştı.
Bu okul, askerî mühendisleri özellikle kale ve savunma yapıları tasarlamak için yetiştiriyordu. O dönemde bu tür tahkimatlar, savaş stratejisinin temel unsurlarıydı. Duvarların, top ve tüfek ateşine dayanacak kadar yüksek inşa edilmesi gerekiyordu.
Gerekli yükseklik, çevredeki arazinin ölçümleriyle hesaplanmaktaydı. Ancak bu oldukça zahmetli bir süreçti; birçok gözlem noktasının konumunun dikkatlice hesaplanmasını gerektiriyordu. Monge, bu süreci kökten değiştiren bir fikir geliştirdi. Arazideki en yüksek noktaları belirleyip, bu noktalardan geçen teğet düzlemleri hayal etti. Duvarlar, bu teğet düzlemlerin hemen biraz üzerinde olacak şekilde tasarlanmalıydı.
Bir teğet doğru, bir eğriye tek bir nokta temas eder. Teğet düzlem ise aynı şeyi üç boyutta yapar. Bir eğrinin herhangi bir noktasında teğet bulmak için türevini alırız. Aynı yöntem, yüzeylerin teğet düzlemlerini bulmakta da işe yarar.
Bugün bize basit gelen bu fikir o dönemde devrim niteliğindeydi. Fransa, Monge’un buluşunu askerî tahkimat tasarımı için o kadar önemli buldu ki, uzun süre devlet sırrı olarak sakladı.

Bu yöntem özellikle yıldız biçimli kalelerin tasarımında kullanıldı. Bu kaleler, top atışlarına dayanıklı olacak şekilde geniş tabanlı ve açılı duvarlara sahipti. Bu açılı yapılar, hem düşman ateşini saptırıyor hem de savunmacılara yandan ateş etme olanağı tanıyordu. Önceki yuvarlak duvarlı kalelerde görülen “kör noktalar” böylece ortadan kalktı.
Fransız Devrimi’nden sonra Monge ders notlarını geliştirerek 1798’de Géométrie descriptive adlı kitabını yayımladı. Aynı dönemde kurulan École Polytechnique’in kuruluşunda da etkin rol oynadı.
Sonuç olarak
Monge ayrıca daha sonra 20. yüzyılda yeniden ele alınacak bir problemi de ortaya koydu. Diyelim ki elinizde birkaç kum yığını ve doldurulması gereken birkaç çukur var. Bu kumları çukurlara en verimli biçimde nasıl taşırsınız?
Farklı yollar mümkündür, ama en iyisi hangisidir? Bu, bir optimizasyon problemidir. Monge, kalkülüsün araçlarını kullanarak minimum değerleri buldu; en az iş ya da en düşük taşıma maliyetini sağlayan düzeni belirledi. Bu fikir, günümüzde ulaşım ağlarının temelini oluşturan optimizasyon teorisine ilham verdi.
Kaynaklar ve ileri okumalar
- Chondros, Thomas. (2021). The development of mechanics and engineering design and machine theory since the rennaissance. FME Transactions. 49. 291-307. 10.5937/fme2102291C.
- Migliari, Riccardo. (2012). Descriptive Geometry: From its Past to its Future. Nexus Network Journal. 14. 10.1007/s00004-012-0127-3.
- J. J. O’Connor and E F Robertson, Gaspard Monge, Mac Tutor History of Mathematics website, https://mathshistory.st-andrews.ac.uk/Biographies/Monge/
Matematiksel