Dünyanın sayısız gelenek ve kültürel alışkanlığı içinde belki de en zarif ve en estetik olanı, Japon tapınak geometrisi olarak bilinen sangaku geleneğidir.

1639 ile 1854 yılları arasında Japonya, Batı dünyasından kendi isteğiyle tamamen izole yaşadı. Batı kültürüne ait her tür bilgiye erişim kısıtlandı; bilimsel düşüncenin ülkeye girişi neredeyse tamamen durduruldu. Bu içe kapanma döneminde, özgün bir Japon matematiği doğdu ve gelişti.
Matematikle ilgilenen samuraylar, tüccarlar ve çiftçiler birçok geometri problemi çözdü. Sonuçlarını özenle boyadıkları ahşap levhalara yazdılar ve bu levhaları tapınakların çatılarının altına astılar. Sangaku sözcüğü zaten “matematik tableti” demektir.

Bu levhalar bazen bir ilahi güce teşekkür amacıyla adak olarak sunuldu. Bazen de diğer ibadet edenlere “Bunu çözebiliyorsan dene bakalım.” gibisinden bir meydan okuma anlamı taşıdı.
Sangaku Matematiği Ne İle İlgiliydi?
Sangaku problemleri genellikle klasik Öklid geometrisiyle ilgilidir, ancak Batı’daki tipik lise geometrisi sorularından farklı bir karakter taşır. Daireler ve elipsler bu problemlerde çok daha önemli bir yer tutar. Dairelerin içinde elipsler, elipslerin içinde daireler bulunur.
Bazı sorular oldukça basittir ve yeni başlayan öğrenciler tarafından çözülebilir. Bazı problemler ise neredeyse imkânsızdır ve modern geometrisyenler bu tür sorularla çalışırken kalkülüs ve afin dönüşümler gibi ileri yöntemler kullanır.

Sangaku geleneğini kimin ve ne zaman başlattığını merak etmek doğaldır. Ancak bu soruları sormak, yanıtlamaktan daha kolaydır. Tapınaklara levha asma geleneği, sangaku ortaya çıkmadan yüzyıllar önce Japonya’da zaten vardı.
Japonya’nın yerel inancı olan Şintoizm, “sekiz yüz bin tanrı” olarak anılan kamilerle doludur. İnanca göre kamiler atları sever. Bu nedenle, tapınağa adak olarak canlı bir at sunamayan kişiler, bunun yerine ahşap üzerine çizilmiş bir at figürü armağan ederdi. Bu gelenek sonucunda 15. yüzyıldan kalma birçok ahşap levha günümüze ulaşmıştır.
Sangaku levhalarının en eskisi de Tochigi Eyaleti’nde bulunmuştur ve 1683 yılına tarihlenir. Bir başka sangaku levhası Kyoto’dan gelir ve 1686 tarihini taşır. Üçüncü bir levha ise 1691 yılına aittir. Bu nedenle tarihçiler, geleneğin ilk olarak 17. yüzyılın ikinci yarısında ortaya çıktığını düşünür.
Batı Dünyası Sangaku İle Yakın Zamanda Tanıştı
Günümüzde 880’den fazla sangaku levhası korunmuş durumdadır. Bu levhaların dağılımına bakıldığında, Japonya’nın hem kırsal hem kentsel bölgelerinde oldukça eşit biçimde yayıldıkları görülür.

Günümüze ulaşan sangaku levhalarının çoğu birden fazla teorem içerir ve genellikle canlı renklerle boyanmıştır. Teoremlerin kanıtları genellikle verilmez, yalnızca sonuçlar yazılır. Bunun dışında levhada çoğunlukla sunan kişinin adı ve tarih yer alır. Tüm problemler yalnızca geometriyle ilgili değildir. Bazıları farklı cisimlerin hacimlerinin hesaplanmasını ister ve bu tür sorular kalkülüs bilgisi gerektirir.
Günümüzde sangaku geleneği, geleneksel Japon matematiğine ilgi duyan birkaç kişi dışında büyük ölçüde unutulmuştur. Bu az sayıdaki meraklı arasında, lise öğretmeni Hidetoshi Fukagawa da vardır. Yaklaşık otuz yıl önce Fukagawa, eski bir kütüphane kitabında matematik levhalarına dair bir notla karşılaştı ve büyük bir şaşkınlık yaşadı. Çünkü o zamana kadar böyle bir gelenekten hiç haberi olmamıştı.

Bu keşiften sonra, Japonya’nın birçok bölgesine seyahat ederek bu levhaları inceledi. Zamanla yalnızca sangaku hakkında değil, geleneksel Japon matematiğinin tamamını kapsayan zengin bir kitap koleksiyonu oluşturdu.
Bir Sangaku Örneğine Bakalım
Bu problem, Gunma Eyaleti’nde bulunan 1874 tarihli bir sangaku levhasından alınmıştır. Büyük bir mavi daire, bir karenin içine yerleştirilmiştir. Karenin kenarlarına ve mavi daireye değen, farklı yarıçaplara sahip dört küçük turuncu daire vardır. Soru şudur: Bu dört küçük dairenin yarıçapları ile karenin bir kenarının uzunluğu arasında nasıl bir ilişki vardır?
İpucu: Bu problem, dört dairenin bir beşinci daireye ya da bir doğruya teğet olduğu durumlar arasındaki ilişkiyi tanımlayan Casey Teoremi kullanılarak da çözülür.
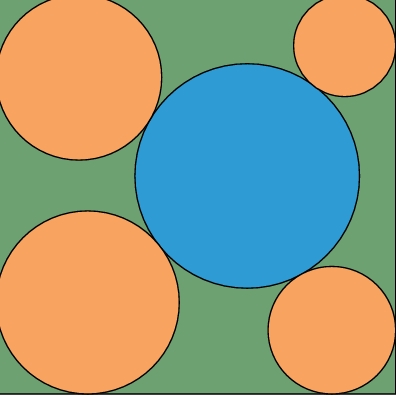
Cevap: Karenin bir kenarının uzunluğu a olsun. Sağ üst, sol üst, sol alt ve sağ alt köşelerdeki turuncu dairelerin yarıçaplarını sırasıyla r₁, r₂, r₃ ve r₄ olarak adlandıralım. Bu durumda ilişki şu biçimdedir:
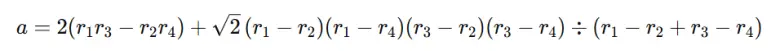
Sonuç Olarak
Bazı sangaku levhalarının, yalnızca geometrinin güzelliğinden büyülenen sıradan matematik meraklıları tarafından yapıldığını düşünmek insana mutluluk verir. Belki de bir köy öğretmeni, gün boyunca öğrencileriyle çalıştıktan sonra ya da bir samuray, kılıcını bileyledikten sonra odasına çekilir, yağ lambasını yakar ve küreler ile elipsoidleri içeren karmaşık bir probleme dalardı.
Sonunda çözümü bulduğunda kısa bir ara verip emeğinin karşılığını çıkarmanın tadını çıkarırdı. Kanıtın, kendisine rehberlik eden ruhlara sunulmaya değer bir armağan olduğuna inanırdı. Teoremi bir ahşap levhaya işlettirir, onu yerel tapınağa asar ve bir sonraki sorunu düşünmeye başlardı.
Tapınağı ziyaret edenler, renkli levhayı fark eder ve güzelliğine hayran kalırdı. Çoğu, yazarın bu kadar şaşırtıcı bir sonuca nasıl ulaştığını merak ederek ayrılırdı. Bazıları problemi çözmeyi ya da geometriyi öğrenmeyi denerdi. Kimi ziyaretçilerse akıllarında yeni bir soru taşırdı: “Ya problem biraz değiştirilseydi…” Belki de bu, hepimizin üzerinde düşünmesi gereken bir şeydir.
Kaynaklar ve ileri okumalar
- The Development of Mathematics in China and Japan. Second edition (reprint). Yoshio Mikami. Chelsea Publishing Company, New York, 974.
- Hosking, Rosalie. (2017). Solving Sangaku: A Traditional Solution to a Nineteenth Century Japanese Temple Problem. Journal for History of Mathematics. 30. 10.14477/jhm.2017.30.2.053.
- Chokuyen Naonobu Ajima; Bağlantı: https://mathshistory.st-andrews.ac.uk/Biographies/Ajima/
Matematiksel