Diyelim ki bir seçim yapmanın eşiğindesiniz; örneğin bir ev satın almayı planlıyorsunuz. Seçeneklerinizi sıraladınız ve üçüncü ev neredeyse tüm beklentilerinizi karşılıyor. Ertesi gün anlaşma yapmak için hazır durumdasınız. Ancak akşam olduğunda zihninizi kurcalayan bir soru beliriyor: “Ya sıradaki ev bu evden daha iyiyse?”

Bu ikilem yalnızca ev alırken değil, iş değiştirme ya da ilişkilerde de karşınıza çıkar. İşte tam da böyle durumlarda, matematik ve psikolojinin birleştiği bir kavram olan optimal durma problemi ve onun çözümü olarak görülen %37 kuralı, kararlarınızı daha bilinçli vermenize yardımcı olabilir.
Yüzde 37 Kuralı Nedir?
Yüzde 37 kuralı, son derece basittir. Seçenekler arasında, ilk yaklaşık %37’lik kısmı sadece gözlemle. Ardından, bu seçenekten daha iyi olan ilk seçeneği değerlendir. Böyle bir seçenek yoksa da sonuncusunu seç. Peki neden?
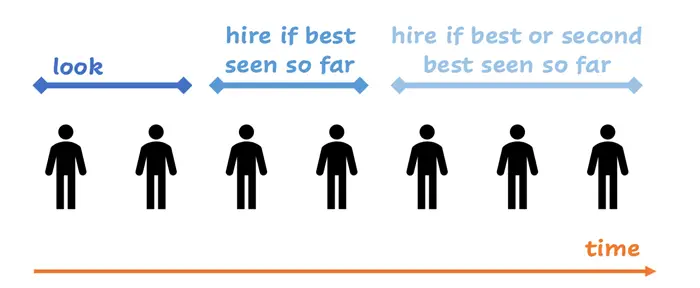
Sözcüklerle anlatıldığında bu oldukça karmaşık ve ulaşılması güç bir problem gibi görünüyor. Ama matematikte işler çok daha nettir.
“Bu temel problemin şaşırtıcı derecede basit bir çözümü var,” diye yazdı matematikçi ve istatistikçi Thomas S. Ferguson, 1989’da. “Öncelikle, yalnızca şu kurallar sınıfına odaklanabileceğimizi gösteriyoruz: r > 1 olmak üzere bir tamsayı seçilir, ilk r – 1 aday reddedilir, ardından gözlemlenen adaylar arasında en iyi olan ilk kişi seçilir.”
Yani, karşınıza rastgele bir adaylar zinciri çıktığında ve siz bu kişiler arasından en iyiyi seçmek istiyorsanız, yapmanız gereken ilk şey şu: herkesi reddedin. Elbette bir noktaya kadar — o noktaya ulaştığınızda, şimdiye kadar gördüğünüz herkesten daha iyi olan ilk kişiyi kabul edersiniz. Şimdi soru şuna dönüşüyor: O nokta ne zaman gelir?
Diyelim ki kaç kişiyi değerlendireceğinizi biliyorsunuz ve bu kişiler sırayla karşınıza çıkacak. Stratejiniz şu: İlk m kişiyi sadece gözlemleyeceksiniz, hiçbirini seçmeyeceksiniz. Sonrasında ise, bu ilk m kişiden daha iyi olan ilk adayı seçip süreci sonlandıracaksınız. Şimdi olası senaryolara bakalım:
Eğer en iyi aday tam (m+1). sıradaysa: Onu hemen seçersiniz ve en iyi seçimi yapmış olursunuz. Peki ya en iyi aday (m+2). sıradaysa? Bu durumda şansınız ikiye ayrılır:
- Eğer (m+1). kişi, ilk m kişiden daha iyiyse ama en iyi kişi değilse, siz onu seçmiş olursunuz. Bu durumda en iyi adayı kaçırırsınız.
- Ama eğer (m+1). kişi önceki m kişiden daha iyi değilse, onu reddeder ve (m+2). kişiye ulaşırsınız. Eğer o en iyiyse, onu alırsınız. Bu ikinci senaryoyu seçelim.
Neden Yüzde 37?
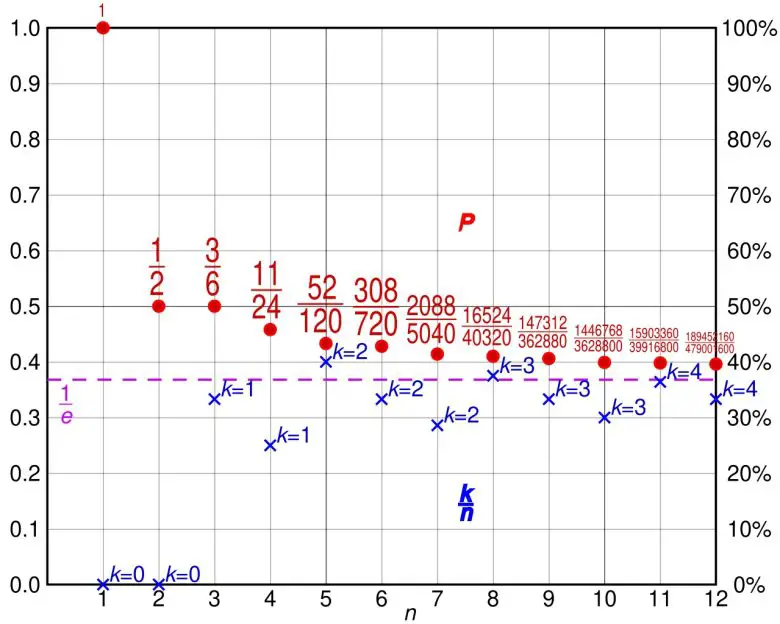
İlk (m+1) kişi içinde, (m+1). kişinin, önceki m kişiden daha iyi olduğu senaryo sayısı toplam olasılıkların sadece 1/(m+1) kadardır. Yani %1/(m+1) olasılıkla kötü senaryoya düşersiniz. Bu da şu demek: %m/(m+1) olasılıkla hâlâ “beklemeye devam eder”. Bu durumda daha iyisini yakalama şansı bulursunuz. Bu desen büyüdükçe de devam eder:
Diyelim ki en iyi aday (m+3). sıradaysa. Bu kişiye ulaşabilmek için, önceki iki aday olan (m+1) ve (m+2). kişilerin, ilk m kişiden daha iyi olmamaları gerekir. Yani, her ikisi de önceki gözlemlerinizin zirvesini geçememelidir. Bu iki kişinin daha önceki adaylardan daha iyi olma olasılığı 2/(m+2) kadardır. Bu durumda, m/(m+2) ihtimalle siz beklemeye devam eder ve en iyi adaya ulaşabilirsiniz.
Buradan genel bir desen ortaya çıkar: Eğer en iyi aday n’inci sıradaysa, onu seçme olasılığınız m / (n – 1) olur. Bu oran, n arttıkça yani aday sayısı büyüdükçe belirli bir değere yaklaşır. Ferguson’a göre, bu olasılıkların toplamı bir Riemann integrali ile temsil edilebilir.
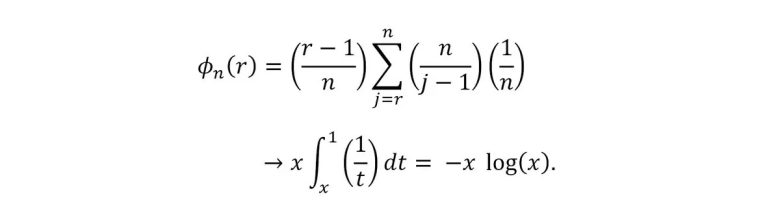
Peki bu stratejiyi en verimli hâle nasıl getirirsiniz? Yapılması gereken şey, m/n oranını 1/e’ye eşitlemektir. Bu da yaklaşık olarak yüzde 36,788’e denk gelir. Yani ilk yüzde 36,788’lik kısmı gözlemleyip reddetmeli, ardından onlardan daha iyi olan ilk seçeneği kabul etmelisiniz.
Sonuç Olarak
Sorun şu ki insan ilişkilerini sayılara dökmek zordur. İnsan davranışındaki kaygan ve belirsiz değişkenleri hesaba kattığınızda, olasılıklar ve oyun teorisi beklenmedik sonuçlar üretir.
Örneğin %37 kuralını düşünün. Ciddi bir karar vermeden önce farklı kişilerle buluşur, çeşitli kişilik tiplerini tanırsınız. Bu yaklaşım mantıklıdır. Ama ilk buluşmanızda hayatınızın aşkıyla karşılaşmadığınızı kimse garanti edemez. Üstelik bu kararı yalnız siz vermezsiniz; karşı taraf da sizi kabul etmek zorundadır. Ayrıca bazen birinin gerçek karakterini tanımak için 10, hatta 100 buluşmaya ihtiyaç duyarsınız.
Yine de %37 kuralı güçlü bir rehberdir. Alışveriş yaparken de hayatınızın en önemli kararlarını alırken de bu matematiksel ilkeyi güvenli bir başlangıç noktası olarak kullanabilirsiniz.
Kaynaklar ve ileri okumalar:
- Wikipedia contributors. (2025, August 16). Secretary problem. In Wikipedia, The Free Encyclopedia. Retrieved 04:44, August 17, 2025, from https://en.wikipedia.org/w/index.php?title=Secretary_problem&oldid=1306151077
- How many people should you date before settling down? Follow the 37% rule. Yayınlanma tarihi: 21 Nisan 2022; Bağlantı: How many people should you date before settling down?/
- Strategic dating: The 37% rule; Yayınlanma tarihi: 1 Mart 2017; Bağlantı: https://plus.maths.org/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





