Maxwell’in Cini ya da şeytanı, termodinamiğin ikinci yasasını ihlal ediyor gibi görünen hayali bir kahramandır. Bilim insanları bu fikrin tam olarak ne anlama geldiği konusunda 150 yıldır tartışıyorlar.
Soğuk bir kış günü elinizde bir fincan çay ile bir kaloriferin yanında ısınmaya çalıştığınız zamanlarda doğanın temel bir gerçeğine minnet duymanız gerekiyor. Bu yasa ısının sıcaktan soğuğa doğru akması ile ilgilidir. Eğer bu olmasaydı üşüyen ellerinizi ısıtma şansınız olmayacaktı. Ayrıca tersi olsaydı, radyatör havadaki az miktardaki ısıyı emecek ve oda daha da soğuyacaktı.
Bu doğa gerçeği hakkında günümüzde bildiklerimiz için Rudolf Clausius, Lord Kelvin ve elbette James Clerk Maxwell’e teşekkür etmeliyiz. Sonuçta günümüzde onlar sayesinde ısının ne olduğunu açıklayabiliyoruz. Ancak ısının doğasına ilişkin bu anlayış bir zamanlar bilim insanlarına yeterince inandırıcı gelmemişti. Bunun üzerine 1867’de Maxwell bir düşünce deneyi tasarladı.

Deney ilk olarak 1867’de Maxwell ve Peter Tait arasındaki bir mektup alışverişinde ortaya çıktı. Daha sonra Maxwell’in 1872’de yayınlanan Theory of Heat başlıklı kitabında yer aldı. Bu düşünce deneyi günümüzde “Maxwell’in Cini / Şeytanı” adı ile biliniyor.
Aslında Maxwell bu deneyi anlatırken cin ya da şeytan kelimesini kullanmamıştı. “Demon” yani şeytan kelimesini ilk kullanan 1874’te Lord Kelvin olarak bilinen William Thomson’dı. Bu nedenle bahsi geçen cin ya da şeytan, kabın içindeki her parçacığın hızını veya kinetik enerjisini dikkatlice analiz eden bir cihaz veya makine için bir metafor olarak düşünülmelidir.
Bu deney yeni araştırma alanlarının ortaya çıkmasına ve uzun tartışmalara neden oldu. Bunun nedeni deneyin doğa yasalarının en önemlilerinden birini konu almasıydı. Bu deney termodinamik yasasının geçerliliğini sorgulamak amacıyla ortaya atılmıştı. Öncelikle deneyi aktaralım.
Maxwell’in Cini Düşünce Deneyi
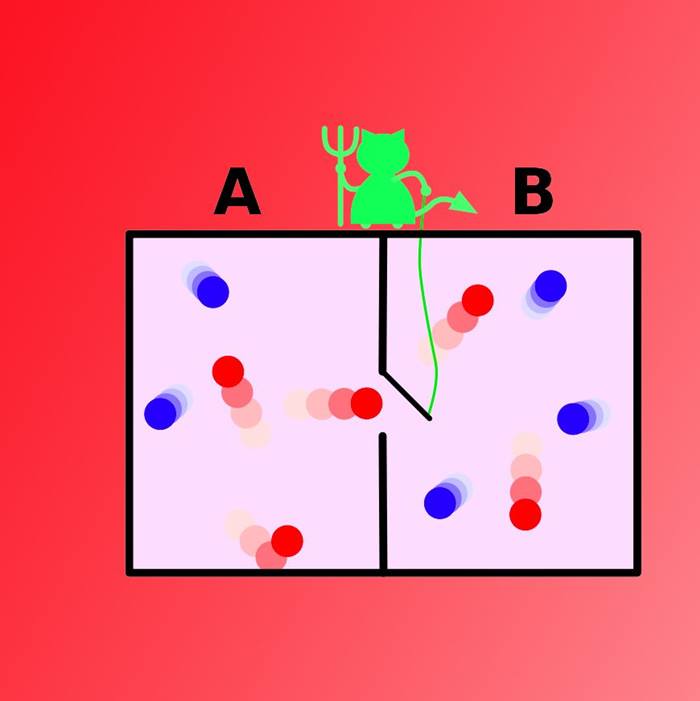
Bildiğiniz gibi, hava olarak bildiğimiz karışım da dahil tüm gazlar, farklı hızlarda rasgele yönlere doğru giden trilyonlarca molekül içerir. Moleküller ortalıkta ne kadar hızlı geziyorlarsa, gaz da o kadar sıcak olur. Düşünce deneyinde Maxwell, gazla dolu bir odayı bir duvar ile dikine doğru iki parçaya bölmeye hayal etti. Bu duvarın ortasında, herhangi bir taraftan bir molekül yaklaştığında hızla açılıp kapanarak molekülün karşı tarafa geçmesine izin veren bir kapakçık vardı.
Normal koşullarda kapakçıktan karşı tarafa geçen moleküllerin bazıları hızlı, bazıları yavaş hareket edenlerden olacaktır. Fakat ortalama hızları belirli bir sıcaklık derecesine karşılık gelir. Bu yüzden iki bölme arasında bir sıcaklık farkı oluşmaz. Şimdi işi içine hayali bir yaratık karıştıralım.
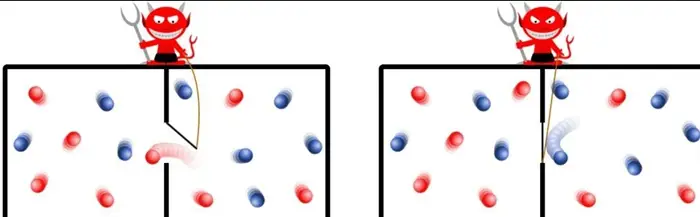
Maxwell’in cini, havadaki molekülleri teker teker gören ve hızlarını ölçen hayali bir yaratık. Her molekül geldiğinde açılıp kapanan kapakçığın kontrolünü o yapıyor. Cin, sol bölmeden sağ bölmeye geçecek moleküllerden sadece hızlı gidenlere kapıyı açıyor; sağdan sola ise sadece yavaş olanlara.
Bunun sonucunda kutunun sağ tarafı daha hızlı hareket eden moleküllerle gitgide dolar daha sıcak olur. Elbette sol tarafta daha soğuk olacaktır. Bu sayede iki bölme arasında bir sıcaklık farkı olur. Bu arada Termodinamiğin İkinci Yasası’nın etkisi altındaki bir süreci tersine çevirerek de yasayı çiğnemiş oluruz.
Peki, bu mümkün müdür? Yüzyıldan uzun zaman boyunca pek çok büyük beyin bu soruya yanıt aradı. Konunun uzun süre revaçta kalmasının altında, devridaim makineleriyle olan bağlantısı yatıyordu. Devridaim makineleri, hiç enerji harcamadan süresiz çalışabilen düzeneklerdir. Eğer Maxwell’in cini İkinci Yasa’yı çiğneyebiliyorsa, biz de mekanik bir düzenekle aynı şeyi yapabiliriz demektir.
Maxwell’in Cini Paradoksunun Çözümü Var mıdır?
Termodinamiğin toplamda dört yasası var. Dördü de ısı ve enerjinin nasıl yer değiştirebileceğiyle ilgilidir. İçlerinde en önemlisi ise İkinci Yasadır. Birinci Yasa bilindik bir gerçeği ifade eder. Enerji bir türden başka bir türe dönüştürülebilir fakat yaratılamaz veya yok edilemez. Birinci Yasanın asıl önemi İkinci Yasanın temellerini oluşturmasıdır. ( Bu arada ayrıca göz atmak isterseniz: Fizikçiler, Termodinamiğin Birinci Yasasını Yeniden Tanımlıyorlar)
Termodinamiğin İkinci Yasası temel anlamda entropiyle ilgili bir önermedir. Bu yasaya göre dışarıdan enerji verilmediği sürece entropi hep artar, hiç azalmaz. En basit tanımı ile entropi dağınıklık ve düzensizliğin ölçüsüdür. Değişim düzenden düzensizliğe doğrudur. Diğer bir deyişle değişim düşük entropiden yüksek entropiye doğru olacaktır.
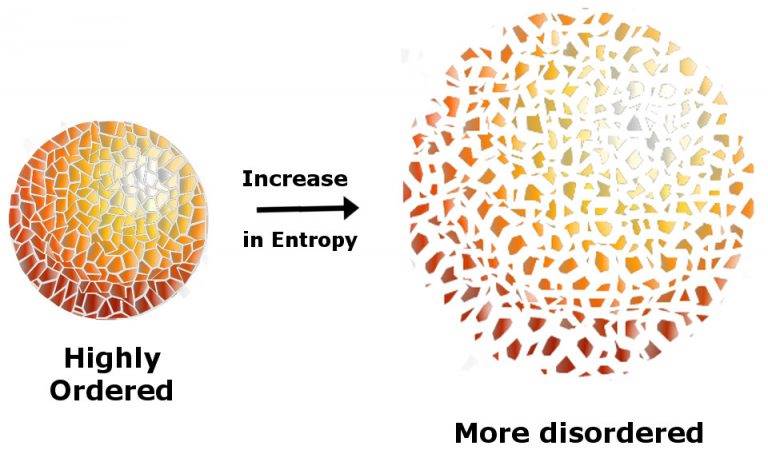
Bunun yanı sıra entropiyi, bir şeyin bir işi yerine getirmek için enerji harcama yeteneği olarak da düşünebiliriz. Bu durumda, enerji harcama yeteneği ne kadar yüksekse, entropi düzeyi o derece düşük olmalıdır. Örneğin kurmalı bir oyuncak kuruluyken entropisi düşüktür; yayı boşaldıkça entropisi artar. Tamamen boşaldığın da, kendimiz enerji harcayarak tekrar kurarız. ( Detaylar için: Entropi Nedir? Termodinamiğin İkinci Yasası Tam Olarak Ne Anlama Geliyor?) Dönelim Maxwell’in Cini’ne…
Maxwell’in Cini İçin Leo Szilard’ın Çözümü
Konu ile ilgili 1929’da Leo Szilard, anahtar bir makale yayınladı. Bu makalede, Maxwell’in cininin değişik bir türünü anlatıyordu. Szilard’ın çözümü İkinci Yasa’nın evrenselliğinin bir onaylamasıydı.
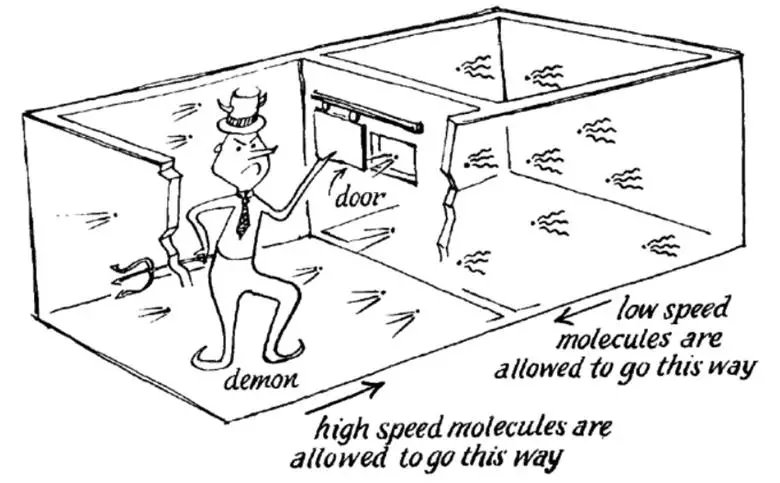
Yukarıda aktardığımız düzeneğe geri dönelim. Kutunun her iki odacığında ellişer tane olmak üzere rastgele dağılmış toplam yüz molekül olsun. Cin, kapakçığı dikkatlice açıp kapatarak bir taraftaki 25 hızlı molekülü sağ tarafa tarafa, sağ taraftaki 25 yavaş molekülü de sol tarafa geçirsin. Bunu yapmak için kapakçığı 50 kez açıp kapaması gerek. Sonuçta bu cinin kapakçığı açıp kaparken harcadığı enerji, ne kadar küçük olursa olsun, entropiyi düşürmek için ödediği bedeldir.
Ancak eğer cinin moleküllerin durumuyla ilgili hiç bilgisi olmasaydı ve kapakçığı 50 kere gelişigüzel açıp kapatarak soldaki moleküllerin yarısının sağa, sağdakilerin yarısının da sola geçişine izin verseydi, bu durumda her iki taraf yine aynı sıcaklıkta olurdu; çünkü sonuçta her iki yönden ortalama olarak eşit sayıda hızlı ve yavaş molekül karşıya geçmiş olurdu.
Demek ki hiçbir bilginin olmadığı durumda, veya bilgi varsa bile kullanılmadığı durumda, entropide bir azalma görmeyiz. Ama cin kapakçığı elli kere açıp kapatarak yine aynı enerjiyi kullanmış oldu. Belli ki kapakçığı hareket ettirmek için gereken çabanın molekülleri ayırma süreciyle bir ilgisi yok.
İşte tam da bu noktada Szilard, bilginin nereye oturtulması gerektiğini buldu. Maxwell’in cini asla tam verimli olmazdı. Moleküllerin yerleri ve sıcaklıkları hakkında bilgi edinebilmek için enerji kullanması gerekirdi. Bu enerji de dış ortamın entropisini arttırırdı.
Cini Yenmeyi Başarmamız Mümkün mü?
21. yüzyılda bu düşünce deneyi bir kaç defa gerçek hayata taşındı. 2007’de bilim insanları bu deneyi ışıkla çalışan bir kapı kullanarak tekrarladı. 2010’da başka bir ekip, iblisin bilgisi tarafından üretilen enerjiyi, kullanmanın bir yolunu tasarladı ve 2016’da bilim insanları, Maxwell’in cini fikrini gaz değil, ışık içeren iki bölmeye uyguladılar. Hatta Fransa’da bulunan École Normale Supérieure de Lyon ‘dan fizikçi Antoine Naert ve meslektaşları, 2022 yılında makroskobik ölçekte çalışabilen böylesine bir makine yaptıklarını iddia ettiler. Ancak evrensel yasalarımız her durumda geçerliliğini korudu.
Kaynaklar ve ileri okumalar
- What Is Maxwell’s Demon?; Yayınlanma tarihi: 4 Ocak 2022; Bağlantı: https://www.scienceabc.com/
- How Maxwell’s Demon Continues to Startle Scientists; yayınlanma tarihi: 22 Nisan 2021; Bağlantı: https://www.quantamagazine.org
- Satanic science. Yayınlanma tarihi: 24 Mart 2014; Bağlantı: https://plus.maths.org/
Matematiksel










