Werner Heisenberg (1901-1976) yirminci yüzyılın en önemli fizikçilerinden biridir. Ancak kuantum kuramının gelişiminde oynadığı büyük rolün yanı sıra, aynı zamanda Almanya’nın atom bombası araştırmalarında da yer alan temel bir figürdür.

Kısaca Werner Karl Heisenberg Kimdir?
Werner Karl Heisenbergdu, 1901 yılında Almanya’da akademisyen bir ailede dünyaya geldi. Babası August Heisenberg, Westphalia’da bir lisede Yunanca, Latince ve filoloji dersleri veren bir eğitmendi. 1909 yılında August Heisenberg’e, Münih Üniversitesi’nde Orta çağ Yunan ve Bizans tarihi profesörlüğü teklif edilince aile oraya taşındı.
Yaşamı boyunca Werner Heisenberg bu kente büyük bir sevgi besledi. Gençliğinde Münih’teki Royal Maximilian Gymnasium’a devam etti, yüksek performansı, yeteneği ve tutkusuyla buradaki tüm öğretmenlerinin beğenisini topladı. Werner’in matematiğe güçlü bir ilgisi ve yeteneği olduğu bu dönemlerde anlaşılacaktı.

Özellikle soyut matematik problemleri Heisenberg’i büyülemekteydi. Kanıtlamaya giriştiği, ancak başarılı olamadığı Fermat’ın son teoremi de bunlar içerisindeydi. Aslında fiziği hiçbir zaman bir meslek olarak düşünmemişti. Onu asıl büyüleyen fiziğin arkasındaki matematikti.
Heisenberg lise mezuniyet sınavlarında matematikte olağanüstü bir başarı gösterdi ve soyut matematik okumak üzere Münih Üniversitesi’ne kaydoldu. Profesör Ferdinand Lindemann’ın derslerine girdiğinde hocası onun hakkında “zaten çok fazla şey bildiği” ve bu yüzden matematik okumasının anlamsız olduğu biçiminde bir değerlendirmede bulundu.
Bu olayın ardından, Heisenberg’in aynı üniversitede ders vermekte olan babası, oğluna fizikçi Arnold Sommerfeld’in derslerini almasını tavsiye etti. Sommerfeld, Niels Bohr’un atom üzerine ilk fikirlerini geliştiren ve onları bugün Bohr – Sommerfeld atom modeli olarak bilinen haline getirmiş kişiydi. Sommerfeld onun parlak bir öğrenci olduğunu derhal anladı.
Werner Karl Heisenberg’in Kuantum Mekaniği İle İlgili Çalışmaları
Klasik biçimde düşünme eğitimi almış eski fizikçilerin aksine Heisenberg, fizikteki iki yeni kuramsal yaklaşımdan biri olan (diğeri Einstein’ın göreliliği) kuantum mekaniği alanında hızlıca düşünebilme ve meseleleri kavrayabilme yetisine sahipti. Aynı üniversitede okuyan ve ileride kuantum kuramına önemli katkılar yapacak olan başka bir öğrenci de Wolfgang Pauli’ydi. Heisenberg’le ikisi yakın dosttu.

Sommerfeld ders vermek üzere bir dönemliğine Wisconsin Üniversitesine gidince Heisenberg Göttingen’de bu süreyi Max Bom’la çalışarak geçirdi. Born hemen, Heisenberg ve diğer asistanı Pascual Jordan’la birlikte matrisler üzerine kurulu kuantum mekaniğini formüle etmeye girişti. Sonuçta Göttingen’de üç imzalı ünlü “matris mekaniği” yani matris tabanlı kuantum kuramı makalesi ortaya çıktı.
Sommerfeld döndüğünde Münih’teki doktorasını tamamlamıştı.1926 yılında Heisenberg, fizik alanında ileri gelen bir otorite olan Bohr’la çalışmak üzere Kopenhag’a gitti. Heisenberg belirsizlik ilkesini bu sırada formüle etti. Bohr’un evinde gerçekleşen çok sayıda tartışmanın sonucunda kuantum kuramının “Kopenhag yorumu” yine burada ortaya çıktı.
Heisenberg’in belirsizlik ilkesi nedir?
Aslına bakarsanız “Breaking Bad” dizisi Heisenberg adını kamuoyuna yeniden tanıtana kadar, Alman bilim insanı özellikle belirsizlik ilkesiyle tanınıyordu.

Ona göre bir parçacığın hem momentumu hem de konumu aynı anda kesin biçimde ölçülemezdi ve bu kullanılan aletin yeterliliğinden bağımsız bir doğruydu. Eğer biri tam olarak biliniyorsa, diğeri ister istemez bir belirsizlik içerecekti.
Heisenberg bu özelliğin atomlar, moleküller, elektronlar, protonlar, nötronlar vb olmak üzere atom-altı parçacıkların mikro dünyasının tümü için geçerli olduğunu iddia etti. Bu keşfini içeren 14 sayfalık bir mektubu 1927’de Pauli’ye gönderdi. Bu mektup daha sonradan, ünlü “belirsizlik ilkesi”ni dünyaya duyurduğu ilk yazılı belge olacaktı.

Tümüyle kuantum mekaniğinin matematiksel bir sonucu olan belirsizlik, aslında tek bir basit denklemle ifade edilen basit bir ilkedir. Detaylar burada: Çoğunlukla Yanlış Anlaşılan Heisenberg Belirsizlik İlkesi Nedir?
1927 Eylül ayında içlerinde Bohr, Heisenberg, Fermi, Schrödinger ve Pauli’nin yer aldığı kuantum fizikçileri yeni fizik üzerine tartışma amacıyla İsviçre-ltalya sınırındaki Como Gölü kıyısında bir konferansta bir araya geldiler. Ardından birçoğu Brüksel’e geçerek o yılki gündemi kuantum fiziğine ayrılan Solvay Konferansı’na katıldı.

Nobel Fizik Ödülü ve Savaş Zamanları
Heisenberg kuantum mekaniği üzerine çalışmaları nedeniyle 1932 yılında Nobel Fizik ödülünü aldı. Ödül fizik dalında 1933 yılı Nobel ödülleriyle birlikte açıklandı. O yılın ödülü de Schrödinger ile İngiliz fizikçi Paul Dirac arasında paylaştırıldı.
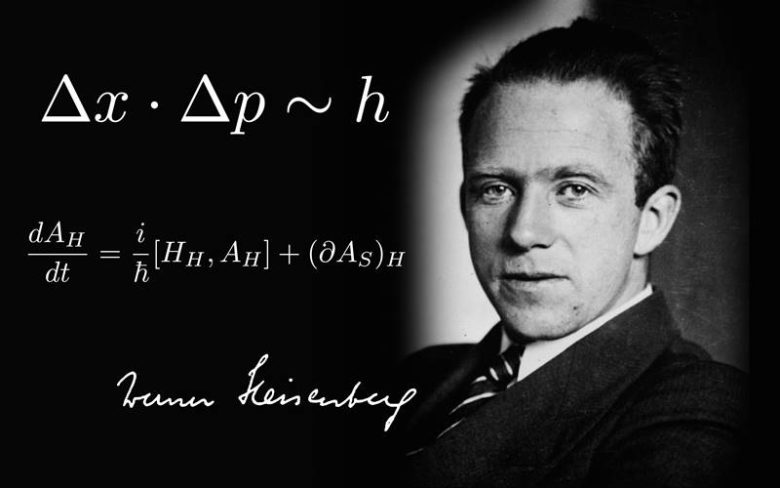
1933 yılına damgasını vuran bir diğer gelişme ise Almanya’da Hitler’in iktidara gelişiydi. Kısa süre içerisinde üniversite ortamı büyük değişimlere sahne oldu. Hitler Yahudi bilim insanlarına dönük bir saldırı kampanyasına başladı. Heisenberg ‘Deutsche Physik’ (Alman Fiziği) hareketine karşı çıktığı için bir dizi karalama kampanyasının hedefi oldu. Mektup ve notlarından onun Almanya’daki gelişmelerden dolayı üzüntü duyduğunu biliyoruz.
Bu sırada kendisinden on üç yaş daha küçük Elisabeth Schumacher’le karşılaştılar. Birkaç ay içerisinde evlendiler ve bir yıl sonra önce ikizleri, ardından bir üçüncü çocukları oldu. Her ne kadar etrafında kendisine Yahudi arkadaşları olduğu için yapılan sataşmalar devam etse de bir ailesi olduğu için Almanya’yı terk etmek istemedi.

1938’in sonunda Berlin’de fisyonun keşfi sadece Almanya’daki fizik topluluğunun değil, Alman ordusunun da dikkatini çekecekti. Bu süreçte atom bombası üretmesi için Almanya Werner Heisenberg’e güveniyordu. Bu sıralarda Heisenberg Amerika’da bir seyahatteydi. Dünyanın en iyi fizikçilerinin çoğunluğu o dönem ABD veya Britanya’ya yerleşmişti. Heisenberg’e de kendilerine katılması için çağrı yapıp duruyorlardı. Ama yine de Heisenberg her öneriye hayır diyerek, ülkesinin kendisine ihtiyacı olduğunu söyleyecekti.
Werner Karl Heisenberg ve nükleer silahlanma süreci
Sonucunda o ve bir grup fizikçi Almanya’nın atom bombası üretimi için her olasılığın peşinden azimle gittiler. 1939’dan 1945’e kadar Almanya kendi nükleer programlarını yürüttü. Bir atom bombası yapma umuduyla nükleer reaktörler tasarlayan ve inşa eden iki çalışma grubu vardı. Bu grupların birinin başında Werner Heisenberg, diğerin de ise Kurt Diebner vardı.
Heisenberg’in grubu, bir atom bombasında kullanılmak üzere plütonyum oluşturmak için ağır suya batırılmış bir grup uranyumu harekete geçirebileceğini umuyordu. Bu süreçte Heisenberg yalnızlaşmıştı. Sonucunda önceden, içlerinde Einstein, Bohr, Schrödinger, Fermi ve Meitner’in yer aldığı uluslararası fizikçiler takımının bir parçasıydı. Şimdi ise ülkesine sadık ama beraberinde yalnızdı. Savaş bilgi akışını kestiği için Amerika ya da İngiltere’de hangi gelişmelerin yaşandığından da habersizdi.

1941 yılında Kopenhag’ta Werner Heisenberg ve Niels Bohr arasında gerçekleşen ünlü toplantı bilim tarihi açısından çok önemlidir. Ancak hakkında fazla şey bilinmemektedir. Kimileri bu toplantının savaşın sonucunu etkilemiş olabileceğine bile inanmaktadır.
İkinci atom bombasının atıldığı haberinin ardından kaydedilen konuşmalarının birinde Heisenberg şöyle diyecekti. “Nasıl yaptıklarını tüm ayrıntılarıyla kafamda canlandırabiliyorum. Aslına bakarsanız bunun fiziği çok basit, tüm mesele tamamen endüstriyel.” Almanya’nın bir atom bombası üretememe nedeni ona göre ağır su üreten tüm fabrikaların tahrip edilmesiydi.
İkinci Dünya Savaşı’ndan sonra Heisenberg Almanya’ya döndü ve saygın bir fizikçi olarak çalışmaya devam etti ve 1976’da 75 yaşında öldü. Ondan geriye, ne olacağından asla emin olamayacağımız bir dünyanın matematiksel bir tanımı kaldı.
Kaynaklar ve İleri Okumalar:
- Heisenberg, the Quantum Philosopher. Yayınlanma tarihi: 5 Aralık 2015. Bağlantı: Heisenberg, the Quantum Philosopher
- Werner Heisenberg; https://www.nobelprize.org/
- Todorov, Ivan. (2005). Werner Heisenberg (1901-1976).
Matematiksel









