Dünyanın en zeki insanı olarak tanınmak, yalnızca bir testten alınan yüksek bir skorla açıklanabilir mi? Yoksa bu unvan, insan zihninin sınırlarını zorlayan daha derin ve kapsamlı bir yeteneği mi yansıtır? Terence Tao, bu soruya adeta hayatıyla yanıt veriyor.

IQ’su 230 olarak ölçülen Tao, “Matematiğin Mozart’ı” olarak anılıyor. Onun dehası yalnızca sayılarla sınırlı değil; karmaşık fikirleri sade, zarif ve anlaşılır bir biçimde ifade etme becerisine de dayanıyor.
1985 yılına ait bir fotoğrafta, henüz on yaşında bir çocuk, büyük matematikçi Paul Erdős’ün yanında oturuyor. İkisi de bir matematik problemi üzerine düşünürken görülüyor. Erdős, gençlerle iletişim kurmayı seven bir bilim insanıydı. Ancak bu sahne kurgu değildi. İkili gerçekten derin bir matematiksel tartışma yürütüyordu. O çocuk, Terence Tao’ydu.

Terence Tao, 1986 Uluslararası Matematik Olimpiyatı’na katıldığında henüz on yaşındaydı. İlk yılında bronz, ertesi yıl gümüş, on üç yaşında ise altın madalya kazanarak, olimpiyat tarihinde üç madalyayı da en genç yaşta alan kişi oldu.
Tao, on altı yaşında üniversiteden mezun oldu, yirmi bir yaşında doktorasını tamamladı ve yirmi dört yaşında Kaliforniya Üniversitesi, Los Angeles’ta (UCLA) profesör unvanı aldı. Günümüzde hâlâ çağımızın en üretken ve etkili matematikçilerinden biri olarak kabul ediliyor.
Terence Tao Kimdir?
Terence Tao, 17 Temmuz 1975’te Avustralya’da doğdu. Babası Billy Tao, üstün yetenekli çocukların eğitimi ve otizm üzerine araştırmalar yapan bir çocuk doktoruydu. Annesi Grace Tao ise Hong Kong’da doğmuş, fizik ve matematik eğitimi almıştı. Billy ve Grace, Hong Kong Üniversitesi’nde tanışmış ve 1972 yılında Avustralya’ya göç etmişti.
Terry, ailenin en büyük çocuğuydu. Ondan iki yaş küçük Trevor ve dört yaş küçük Nigel adında iki kardeşi vardı. Her iki kardeşi de onun gibi son derece yetenekliydi.

Trevor, iki yaşında otizm tanısı almasına rağmen hem matematikte hem de müzikte olağanüstü başarı göstermiştir. Adelaide Üniversitesi’nde matematik, bilgisayar bilimi ve müzik alanlarında çift ana dal yapmış; aynı zamanda uluslararası satranç ustası unvanını kazanmıştır. Nigel ise bilgisayar biliminde doktora yapmış ve sonrasında Google’da çalışmaya başlamıştır.
Terry’nin olağanüstü yeteneği henüz iki yaşındayken fark edildi. Ailesi, onu beş yaşındaki çocuklara okuma ve toplama öğretirken görünce şaşkına döndü. Bu becerileri nasıl öğrendiğini sorduklarında ise yalnızca “Susam Sokağı’nı izledim” diye yanıtladı. Üç buçuk yaşında özel bir okula başladı, ancak öğretmenler onunla nasıl ilgileneceklerini bilemedikleri için okuldan alındı. Beş yaşına geldiğinde normal eğitime başladı.
14 yaşında Flinders Üniversitesi’nde tam zamanlı öğrenci oldu. Henüz 15 yaşındayken ilk kitabını yazdı. 1992’de yüksek lisansını tamamladı ve ardından ABD’ye giderek Princeton Üniversitesi’nde doktora çalışmasına başladı.

1996’da doktorasını tamamladı ve UCLA’da önce yardımcı profesör olarak görev yaptı, ardından 24 yaşında üniversitenin en genç profesörü unvanını kazandı. 2002’de NASA’da mühendis olarak çalışan Laura ile evlendi ve William ile Madeleine adında iki çocuğu oldu.
Terence Tao Hangi Konularda Araştırma Yapıyor?
Terence Tao’nun çalışma alanı yalnızca bir konuyla sınırlı değildir. Tıpkı çocuklukta tanıştığı Paul Erdős gibi, Tao da dünyanın dört bir yanından sayısız matematikçiyle işbirliği yapar. Bugüne kadar, farklı araştırmacılarla birlikte yazdığı 300’ü aşkın bilimsel makaleye imza atmıştır. Şimdi, bu olağanüstü matematikçinin bugüne dek gerçekleştirdiği bazı önemli keşiflere yakından bakalım.
Green–Tao Teoremi
2004 yılında Terence Tao, yakın arkadaşı Ben Green ile birlikte asal sayılarla ilgili yüzyıllardır çözülemeyen bir probleme önemli bir katkı yaptı. Bu çalışma, “ikiz asallar” olarak bilinen asal sayı çiftleriyle ilişkilidir.
İkiz asallar, aralarındaki fark 2 olan asal sayılardır. Örneğin 5 ve 7 ya da 17 ve 19 bu tanıma uyar. Küçük sayılarda bu çiftleri sıkça görebiliriz, ancak sayılar büyüdükçe asal sayılar giderek seyrekleşir. “İkiz asal sayılar varsayımı”, bu tür asal çiftlerinin sonsuz sayıda olup olmadığını sorgular.
Tao ve Green, bu probleme doğrudan yaklaşmak yerine, asal sayılar içindeki başka bir düzeni incelemeye karar verdiler: aritmetik dizilerdeki asal sayı dizilerini. Bu tür dizilerde, asal sayılar arasında sabit bir fark vardır. Örneğin 3, 7 ve 11 sayıları arasında fark 4’tür; bu üçlü, asal sayılardan oluşan kısa bir aritmetik dizidir. Bu dizi 17’de sona erer, çünkü bir sonraki sayı artık bu farkı korumaz.
Green ve Tao, yaptıkları çalışma sonucunda bir sonuç elde etti. Yeterince ileriye giderseniz, asal sayılar içinde istediğiniz uzunlukta düzenli bir dizilim mutlaka vardır. Bu keşif modern matematiğin en çarpıcı ilerlemelerinden biri olarak kabul edilmektedir.
Erdős uyuşmazlık problemi (Erdős discrepancy problem)
Tao’nun üzerinde çalıştığı bir diğer önemli problem, Paul Erdős’ün 1932 civarında ortaya attığı bir varsayıma dayanır. Problem, “işaret dizisi” adı verilen sonsuz bir sayı dizisiyle ilgilidir. Bu dizi, sürekli olarak +1 ve -1 değerlerinin ardışık biçimde yer aldığı basit bir dizidir: (1, -1, 1, -1, 1, -1, …).
İlk bakışta, bu dizinin toplamı sıfır olmalıymış gibi görünür çünkü pozitif ve negatif birler birbirini dengeler. Erdős’ün sorusu, bu düzeni bozduğumuzda ne olacağıyla ilgilidir. Diyelim ki dizideki bazı sayıları atlayarak ilerliyorsunuz; örneğin, her 2. ya da 3. sayıyı seçiyorsunuz ve bir noktada duruyorsunuz. Bu durumda, topladığınız sayıların toplamı hâlâ sıfır mı olurdu?
Erdős, bu sorunun cevabının hayır olduğunu öne sürdü. Ona göre, hangi aralıkları ve ne kadar uzun bir dizi seçerseniz seçin, sonunda toplam sıfırdan farklı bir değere ulaşır. Üstelik bu fark, her zaman belirli bir sayı C’den büyük olmalıydı. Erdős, bunun her zaman olacağını iddia etti ama kanıtlayamadı. Bu varsayımı kanıtlayana 500 dolarlık bir ödül vadetmişti.

Yaklaşık seksen yıl sonra, Terence Tao bu problemi kesin olarak çözdü. Tao, hangi sıçrama düzeni seçilirse seçilsin, dizinin toplamının mutlaka sıfırdan uzak bir değere ulaşacağını kanıtladı. Böylece Erdős’ün sezgisel olarak doğru olduğuna inandığı bu fikir nihayet matematiksel kesinliğe kavuştu.
Döşeme Problemi
Terence Tao’nun çözdüğü bir diğer ünlü problem, hem çok eski hem de son derece estetik bir konuyla ilgilidir. Problem, belirli şekillerin bir düzlemi boşluk bırakmadan ve üst üste gelmeden tamamen kaplayıp kaplayamayacağını inceliyordu.
Bu tür düzenli döşemelere “periyodik döşeme” denir. Yani şekiller, belli bir düzende tekrar ederek tüm düzlemi kaplar. Bu düzen, döndürme, yansıtma ya da kaydırma gibi işlemlerle elde edilebilir.
Bu konuya ilişkin sistematik araştırmalar Johannes Kepler’e kadar uzanır. İki yüzyıl sonra, 1891’de Rus kimyager Yevgraf Fyodorov, her periyodik döşeme düzeninin yalnızca on yedi farklı simetri grubuna ait olabileceğini göstermiştir.
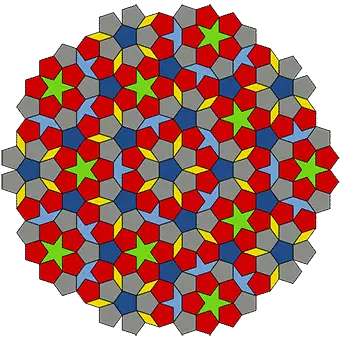
1960’lara kadar her şey gayet düzenli görünüyordu. Ta ki matematikçiler beklenmedik bir keşif yapana kadar. Bazı özel şekiller, düzlemi boşluk bırakmadan kaplayabiliyordu, fakat bunu tekrarsız, yani aperiyodik bir biçimde yapıyorlardı.
Bu durum oldukça şaşırtıcıydı. Çünkü periyodik döşemelerde desenler belirli aralıklarla tekrar eder; hangi yönden bakarsanız bakın aynı düzeni görürsünüz. Oysa aperiyodik döşemelerde şekiller yine tüm düzlemi kaplar, ancak hiçbir desen kendini birebir tekrar etmez. Yine bir düzen vardır, ama bu düzen karmaşık bir biçimde gizlenmiştir.
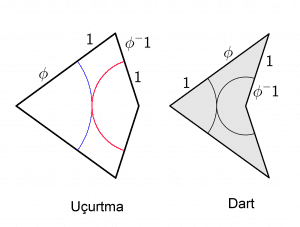
İlk aperiyodik döşeme örneklerinden biri, 20.000’den fazla farklı şekil ile oluşturulmuştu. Matematikçi Roger Penrose bu karmaşayı sadeleştirdi. 1974 yılında yalnızca iki şekille düzlemi tamamen, ama tekrarsız biçimde kaplayabileceğini keşfetti.
Peki, yalnızca tek bir şekil kullanarak, aynı etki elde edilebilir mi? Bu arayış, eğlenceli bir biçimde “einstein” adıyla anılmaya başladı. Buradaki “einstein” Almanca ein Stein, yani “bir taş” anlamına geliyordu.
Yıllar içinde çeşitli çözümler önerildi. Yine de, basit bir şekille düzlemi tekrarsız biçimde kaplamanın yolu bir türlü bulunamamıştı. Bu noktada sahneye Terence Tao ve Rachel Greenfeld çıktı. 2022 yılında tüm matematik dünyasını şaşkına çeviren bir sonuç yayımladılar. Yalnızca ötelemeler kullanarak, çok yüksek boyutlu bir uzayı aperiyodik olarak kaplayan bir “karo” buldular.
Sonuç Olarak

Terence Tao’nun matematikteki olağanüstü başarıları ona sayısız ödül kazandırdı. 2006 yılında, henüz 31 yaşındayken matematiğin Nobel’i olarak kabul edilen Fields Madalyası’na layık görüldü.
Tao’nun aldığı diğer ödüller arasında 2000 yılında Fourier serileri üzerine yaptığı çalışmalar nedeniyle verilen Salem Ödülü ve 2002’de analiz alanındaki araştırmalarıyla kazandığı Bocher Anma Ödülü bulunur. Ayrıca SASTRA Ramanujan Ödülü, Levi L. Conant Ödülü, 2015’te Yılın Atılımı Ödülü, Rolf Schock Matematik Ödülü ve 2020’de İsveç Kraliyet Bilimler Akademisi tarafından verilen onur ödülleri de yer alır.
Kaynaklar ve ileri okumalar
- What Makes for ‘Good’ Mathematics? Yayınlanma tarihi: Kaynak site: Quanta Magazine. Bağlantı: What Makes for ‘Good’ Mathematics?
- Cesare, Chris. (2015). Maths whizz solves a master’s riddle. Nature. 526. 10.1038/nature.2015.18441.
Matematiksel





