Amatör bir matematikçi misiniz? Öyleyse lütfen devam edin. Matematik tarihine hızlıca göz attığınızda, pek çok önemli buluşun, başka alanlarda çalışan ve matematiği yalnızca bir hobi olarak gören kişiler tarafından yapıldığını fark edersiniz. Gelin, tarihin en dikkat çekici amatör matematikçilerinden bazılarına birlikte göz atalım.
1- Marjorie Rice

1975 yılında, San Diego’da bir gün Marjorie Rice, oğlunun Scientific American dergisinde yer alan bir makaleyi okudu. Yazıda, düzlemi tamamen kaplayabilen yalnızca sekiz farklı beşgen şeklin bilindiği belirtiliyordu. Lise düzeyinin ötesinde bir matematik eğitimi olmayan Rice, buna rağmen yeni bir beşgen deseni bulmaya karar verdi.
Döşemeleri takdir etmek için matematikçi olmanız gerekmez. Onlar, neredeyse uygarlık kadar eskidir ve akıl ile mantığın ürünü olmalarının yanı sıra, aynı zamanda birer sanat eseridir. Nitekim, Marjorie Rice da böyle düşünmüş olmalı. Sonucunda birkaç yıl içinde yalnızca bir değil, tam dört yeni döşeme deseni keşfetti. Üstelik bu keşifleri, akademik bir dergide yayımlanacak kadar dikkat çekiciydi.
2- Pierre de Fermat
Amatör matematikçi dendiği anda elbette bir çok kişinin aklına gelecek isim Pierre de Fermat olacaktır. Fermat, 1607 yılında Fransa’nın Beaumont-de-Lomagne kentinde doğdu. Hukuk eğitimi almış ve meslek hayatında hukukçu olarak çalışmış olsa da, matematikle tutkuyla ilgilenen bir amatördü.

Fermat, matematiği yalnızca bir hobi olarak görüyordu. Üzerinde çalıştığı birçok teorem ve denklemi akademik makalelerde değil, meslektaşlarına yazdığı mektuplarda paylaşırdı. Hatta bazı önemli sonuçlarını yalnızca ders kitaplarının kenarına düştüğü notlar şeklinde bırakmasıyla da ünlüdür.
Ancak önemli bir zayıf yönü de vardı. Sık sık çarpıcı sonuçlar ileri sürmesine rağmen, bunların kanıtlarını ya sunmaz ya da yetersiz bırakırdı. Fermat, “Küçük Fermat Teoremi” ile hatırlanacaktır. Ancak elbette ondan çok daha ünlüsü 1994 yılına dek çözülemeyen Fermat’ın Son Teoremi olacaktır.
3- Oliver Heaviside
Çoğu yetişkinin yaptığı işin onları matematiğe yönlendirdiğini söylemesi pek olası değildir. Ancak İngiliz mühendis Oliver Heaviside için bu durum farklıydı.
Heaviside’ın resmi eğitimi, 1860’larda Londra’da başladığı okul yıllarıyla sınırlı kaldı. Okulda son derece başarılı bir öğrenciydi; fakat ailesinin maddi imkânsızlıkları nedeniyle eğitimi 16 yaşında sona erdi.
Bunun ardından, mucit ve iş insanı olan amcasının desteğiyle telgraf endüstrisinde çalışmaya başladı. Ancak maddi sıkıntılar onun öğrenme isteğini bastırmadı. Elektrikçi olarak çalışırken bir yandan da kendi kendine matematik ve fizik öğrenmeye koyuldu.
Başlangıçta çalışmaları, elektrikle ilgili deneysel ve uygulamalı sonuçlara odaklanıyordu. 1870’lerde büyük fizikçi James Clerk Maxwell’in elektrik ve manyetizma üzerine yaptığı çalışmaları okudu. Daha sonra Maxwell’in karmaşık denklemlerini, bugün kullanılan sadeleştirilmiş hâline dönüştüren kişi oldu.
Heaviside’ın matematik ve fiziğe yaptığı katkılar, ona Göttingen Üniversitesi’nden fahri doktora ve Britanya’nın en saygın bilim kurumlarından biri olan Royal Society üyeliği kazandırdı.
Bugün onun mirası, matematikte adını taşıyan Heaviside Fonksiyonu ile yaşamaya devam ediyor. Bu hikâye, kendi kendine öğrenmenin nelere kapı açabileceğini bir kez daha gözler önüne seriyor.
4- Thomas Bayes
Bir sonraki amatör matematikçi Presbiteryen din adamı Thomas Bayes’tir.
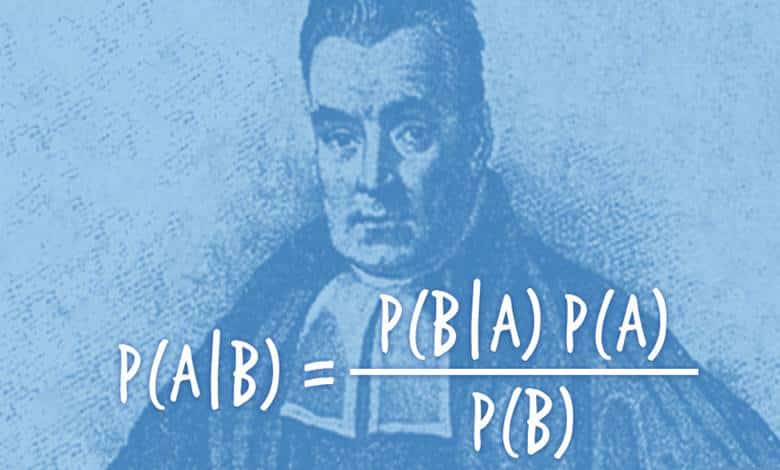
Bayes 1701’de doğdu ve yaşamını matematik ile din arasında kurduğu iki paralel hat üzerinde sürdürdü. Üniversitede mantık ve teoloji okudu. Mezuniyetinin ardından kilisede görev alarak rahiplik yaptı.
Bayes ilk yayımladığı çalışmada teolojik bir konu ele aldı. İkinci eserinde ise Isaac Newton’un kalkülüs kuramını savundu. Bu metni, Piskopos George Berkeley’nin Newton’a yönelttiği eleştirilere yanıt olarak kaleme aldı.
Bayes’i asıl önemli kılan katkı, bugün Bayes Teoremi adıyla bilinen sonuçtur. Olasılık kuramının en temel araçlarından biri olan bu teorem, bir olayın gerçekleşme olasılığını, başka bir olayın gerçekleşmiş olması koşuluyla hesaplamayı sağlar. Bu fikirle Bayes, Bayesçi çıkarım yaklaşımının temelini attı. Bu yaklaşım, olasılığı kullanarak öngörü üretmeyi ve hipotezleri sınamayı mümkün kılar.
Bayes, çalışmaları sayesinde Royal Society üyeliğine seçildi. Günümüzde bilim dünyasında süren Bayesçi–frekansçı tartışmaları, onun matematiksel mirasının hâlâ etkisini koruduğunu gösterir.
5- Marin Mersenne
Son öncü amatör matematikçi, Fermat ile aynı dönemde yaşamış bir başka din adamıdır: Marin Mersenne.

Mersenne 1588’de Fransa’da Oizé yakınlarında doğdu. Le Mans’taki bir Cizvit kolejinde teoloji ve İbranice eğitimi aldı. Daha sonra rahip oldu ve 1610’lu yıllar boyunca felsefe ile teoloji dersleri verdi. Ancak matematik ve müziğe yönelişi daha geç bir tarihte gerçekleşti.
Yaklaşık on yıl sonra Annunciation Manastırı’na yerleştiğinde, bu iki alanda sistemli çalışmalar yapmaya başladı. Üstelik güçlü bir entelektüel çevreye sahipti. Bu dönemde Descartes ve Roberval gibi matematikçilerle, Galileo Galilei ve Huygens gibi fizikçilerle tanıştı.
Mersenne’in ilk önemli matematiksel eseri L’Harmonie Universelle, 1636’da yayımlandı. Bu çalışma, müzik ile matematik arasındaki ilişkiyi ele aldı. Eserde müzik kuramını pratik, teolojik ve biçimsel yönleriyle birlikte inceledi. Kitabın kalıcı etkisi ise Mersenne Yasaları olarak bilinen sonuçlarda ortaya çıktı. Bu yasalar, bir telden çıkan sesin frekansını telin uzunluğu, gerilimi ve kütlesiyle ilişkilendirir.
Buna rağmen Mersenne’i asıl önemli kılan katkı, sayı kuramı üzerindeki etkisidir. Mersenne, biçimindeki sayıları inceledi. Burada p bir asal sayıdır.
Bu sayılara bugün Mersenne sayıları denir. Mersenne, hangi p değerlerinin asal Mersenne sayıları verdiğine dair bir liste sundu. Liste hatalar içeriyordu. Ancak yöntem kalıcı oldu. Bugün bilinen en büyük asal sayı bir Mersenne sayısıdır.
Kaynaklar ve ileri okumalar:
- 5 Amateur Mathematicians Who Revolutionized Math; yayınlanma tarihi: 21 Haziran 2020; Bağlantı: https://famous-mathematicians.com/
- List of amateur mathematicians; Bağlantı: https://en.wikipedia.org/
Matematiksel





