Çoğu insan mantıkla ilk kez lise yıllarında, matematik derslerinde tanışır. Bu derslerde karşılaştıkları doğruluk tabloları, filozof Ludwig Wittgenstein’ın geliştirdiği bir yöntemdir. Wittgenstein, karmaşık önermelerin doğruluk değerlerini sistemli biçimde çözümlemek için bu tabloları tasarlamıştır.

Günümüz mantığında doğruluk tabloları, bir önermenin bileşenleri arasındaki tüm olası doğru–yanlış kombinasyonlarını göstererek mantıksal tutarlılığı test etmenin pratik bir yolunu sunar.
Doğruluk Tablosu Nedir?
Mantıkta, bir şey ifade eden önermeler üzerine kurulu akıl yürütmeler yaparız. Bu tür ifadeler “önermeler” olarak adlandırılır. Bir ifadenin önerme sayılabilmesi için bir iddia taşıması, yani bilgi bildirmesi gerekir. Bu nedenle sorular önerme değildir.
Mantıksal çıkarımlar, önermelerin doğru ya da yanlış oluşuna ve aralarındaki ilişkilere dayanır. Bu ilişkiler “bağlaçlar” olarak adlandırılır ve birden fazla önermeyi birbirine bağlar. Ortaya çıkan ifadenin doğruluğu, bağlı olduğu önermelerin doğruluk değerine göre belirlenir.
Doğruluk tablosu, önermelerin olası doğru–yanlış değerlerini gösteren ve bu değerlerin oluşturduğu akıl yürütmenin geçerliliğini incelemeye yarayan bir çizelgedir.
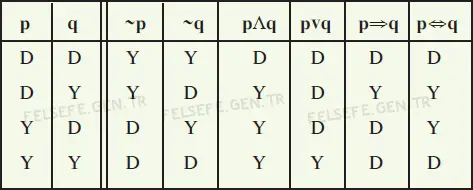
Doğruluk Tablosu Nasıl Doldurulur?
Aşağıdaki temel kuralları bilmek, tablonun satırlarını tek tek yazmak yerine sonuçları zihinsel olarak doldurmamıza yardımcı olur.
- p∨q→ En az biri doğru olduğunda sonuç doğrudur.
- p∧q → Her ikisi de doğruysa sonuç doğrudur.
- p⇒q→ Sadece “doğru → yanlış” olduğunda yanlış olur.
- p⇔q → Her iki önerme aynı olduğunda doğrudur.
Soru: p ∧ ( p ∨ q) ifadesinin en sade şeklini bulunuz.
Çözüm: İç parantezdeki p ve q’nun altına doğruluk değerlerini yazarak başlıyoruz. Şekli inceleyiniz:

Sonra parantez içindeki ∨ bağlacını işliyor ve bulduğumuz sonucu sembolün hemen altına yazıyoruz.
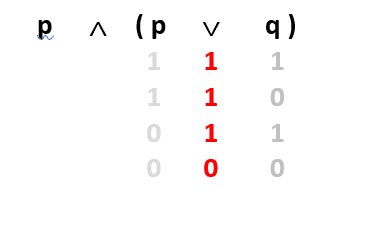
Şimdi en baştaki p’nin altını dolduruyoruz.
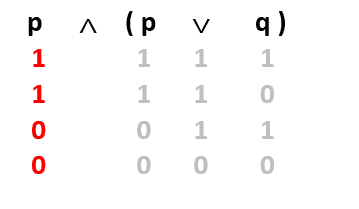
Ve son olarak en soldaki ∧ bağlacının işlemini yaparak sonucunu sembolün altına yazıyoruz.
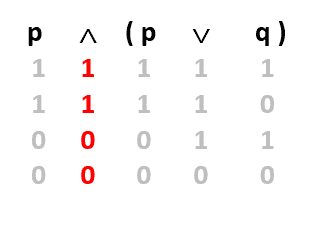
Bulduğumuz sonucun p önermesine denk olduğunu görünüz. O halde sorumuzun cevabı p’dir. Yani p ∧ ( p ∨ q)=p biçimindedir. Aynı şeyleri üç önerme için de yapabiliriz.
Soru: p ⇒ [ p ∨ ( p‘ ∧ r)] ∧ q ifadesinin en sade halini bulunuz.
Çözüm: Sütunları doldurmaya en içteki parantezden başlıyoruz. Şekli inceleyiniz:
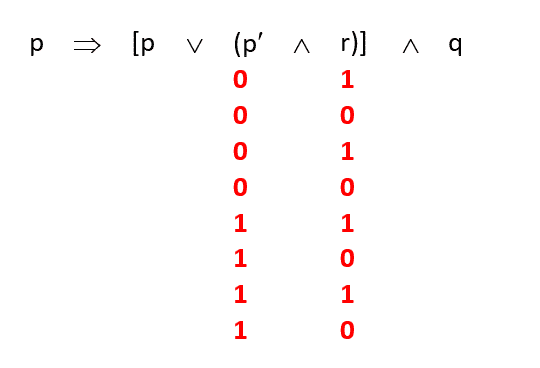
Sonraki adım ∧ bağlacının altına işlem sonucunu yazmak:

Şimdi ∨ bağlacının altını doldurabiliriz. Ama önce p’nin altını dolduruyoruz.

Şimdi de veya bağlacı dolduruluyor:
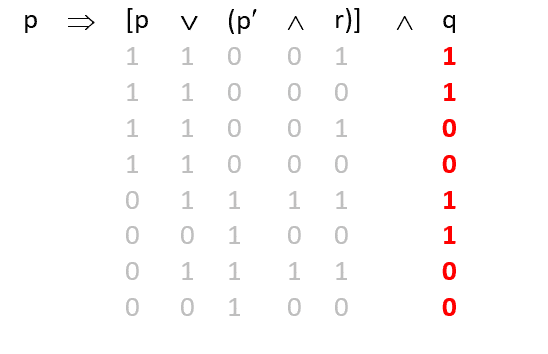
Sıra q’da:
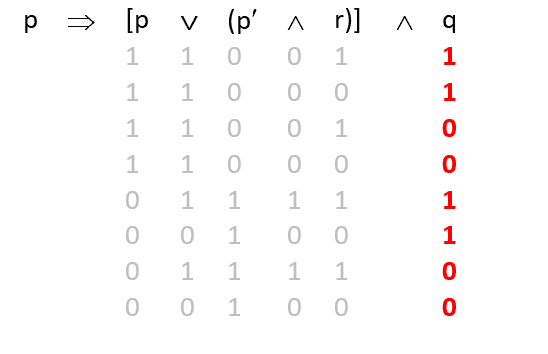
Sıra geldi en sağdaki ve bağlacına.

Şimdi en soldaki p’yi dolduruyoruz:

Ve son olarak ise bağlacını işliyoruz:

Kırmızı sütun işlemin sonucudur. Peki, ama bu sütun hangi önermeye denktir? Biraz dikkatli bakarsak, bunun p ⇒q olduğunu anlarız. O halde sorumuzun cevabı: p ⇒ [ p ∨ ( p‘ ∧ r)] ∧ q = p ⇒ q olur.
Bağlaçları Hatırlamak İçin Kolay Bir Yöntem
Yazımızın bu bölümünde de kısa bir şekilde mantık dersinde kullanılan temel bağlaçları ele alacak ve onlarla yapılan mantıksal işlem sonuçlarını hatırlamanın kolay yollarını göstereceğiz.
Veya: Veya bağlacını toplama işlemi olarak düşünebilirsiniz. (Tabi 1 + 1 = 1 olduğunu kabul etmek şartıyla.)
- 1 ∨ 1 = 1 yani 1 + 1 = 1
- 1 ∨ 0 = 1 yani 1 + 0 = 1
- 0 ∨ 1 = 1 yani 0 + 1 = 1
- 0 ∨ 0 = 0 yani 0 + 0 = 0
Ve: Ve bağlacını çarpma işlemi olarak düşüneceğiz.
- 1 ∧ 1 = 1 yani 1 × 1 = 1
- 1 ∧ 0 = 0 yani 1 × 0 = 0
- 0 ∧ 1 = 0 yani 0 × 1 = 0
- 0 ∧ 0 = 0 yani 0 × 0 = 0
İse: ⇒ bağlacını ≤ olarak düşüneceğiz.
- 1 ⇒ 1 = 1 yani 1 ≤ 1 → 1 (Doğru)
- 1 ⇒ 0 = 0 yani 1 ≤ 0 → 0 (Yanlış)
- 0 ⇒ 1 = 1 yani 0 ≤ 1 → 1 (Doğru)
- 0 ⇒ 0 = 1 yani 0 ≤ 0 → 1 (Doğru)
Ancak ve Ancak: ⇔ bağlacını = olarak düşüneceğiz.
- 1 ⇔1 = 1 yani 1 = 1 → 1 (Doğru)
- 1 ⇔ 0 = 0 yani 1 = 0 → 0 (Yanlış)
- 0 ⇔ 1 = 0 yani 0 = 1 → 0 (Yanlış)
- 0 ⇔ 0 = 1 yani 0 = 0 → 1 (Doğru)
Ya da: Ya da bağlacını ≠ olarak düşüneceğiz.
- 1 ⊻ 1 = 0 yani 1 ≠ 1 → 0 (Yanlış)
- 1 ⊻ 0 = 1 yani 1 ≠ 0 → 1 (Doğru)
- 0 ⊻ 1 = 1 yani 0 ≠ 1 → 1 (Doğru)
- 0 ⊻ 0 = 0 yani 0 ≠ 0 → 0 (Yanlış)
Bağlaçların Pratik Uygulamaları İle İlgili İki Örnek
- Örnek1: 1 ⇒ [ 1∨ (0 ∧ 1)] ∧ 0 işleminin sonucu nedir?
- Çözüm: 1 ≤ [ 1 + (0 × 1)] × 0 = 1 ≤ [ 1 + 0] × 0 = 1 ≤ [ 1 ] × 0 = 1 ≤ 0 = 0 (yanlış)
- Örnek 2: [ 1 ⇒ (1 ⇒ 0) ] ⇒ [ ( 0⇒ 1 ) ⇒ ( 1 ⇒ 1) ] işleminin sonucu nedir?
- Çözüm: [1 ≤ (1 ≤ 0)] ≤ [( 0 ≤ 1 ) ≤ (1 ≤ 1)] = [ 1 ≤ 0 ] ≤ [ 1 ≤ 1 ] = 0 ≤ 1 = 1 (Doğru)
Bu iki yöntem yardımı ile mantık dersindeki sorunlarınızın bir kısmının çözüleceğini düşünüyoruz. Şimdiden kolay gelsin.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel