Gök bilimci, fizikçi ve matematikçi Johannes Kepler, gezegenlerin Güneş etrafındaki hareketini doğru şekilde tanımlayan ilk kişi olmasıyla ünlüdür. Ancak Kepler, matematiksel yeteneğini dünyaya dair bir sorunu çözmek için de kullandı. Hayattaki mutluluğu en üst düzeye çıkarmak istiyorsanız, biriyle ne zaman evlenmek en uygunudur?
Cevap %37 kuralı olarak bilinen şeyi izlemektir: tüm olası seçeneklerin ilk %37’sini reddedin ve ardından, daha önce gelen %37’nin en iyisini aşan ilk kişiyi seçin. Bazıları en iyi seçimlerini gözden kaçıracak olsa da, %37 kuralı matematiksel olarak en üstün stratejidir.
Hayatınızda yalnızca bir kez seçim yapabileceğiniz ve bu seçimle sonsuza dek yaşamak zorunda kalacağınız büyük bir karar söz konusu olduğunda, iki risk ortaya çıkar:
- İlk “iyi” seçeneği kabul edip bununla yetinmeye çalışabilirsiniz. Fakat çok erken seçim yaparsanız, sonradan çıkacak daha iyi bir seçeneği kaybetme riskini de üstlenirsiniz.
- Ya da başta karşınıza çıkan adayları reddedip, her şeyi gölgede bırakacak olağanüstü bir seçeneği bekleyebilirsiniz. Bu durumda sorun, en iyi olasılığın deneyim sürecinizin başında yer almış olmasıdır. Eğer onu geçecek bir aday beklerken bu seçeneği reddederseniz, yalnız kalabilirsiniz.
Peki, tüm diğer etkenler eşit olduğunda, böyle bir durumla karşılaştığınızda stratejiniz ne olmalı:
- çok sayıda farklı aday arasından yalnızca bir seçim hakkınız varsa,
- her bir seçenekle karşılaştıktan kısa süre sonra “evet” ya da “hayır” demek zorundaysanız,
- seçenekleri aynı anda deneme veya reddettiğiniz bir seçeneğe geri dönme hakkınız yoksa,
- ve bir seçeneğe “evet” dediğiniz anda oyun sona eriyorsa?
En iyi stratejiye ulaşmanın cevabı, çoğumuzun beklentisinin aksine, pek çok şeye bağlı değildir. Cevabınızın bağlı olması gereken tek şey, ilgili zaman dilimi boyunca karşılaşmanız muhtemel olan potansiyel seçeneklerin sayısını bilmektir.
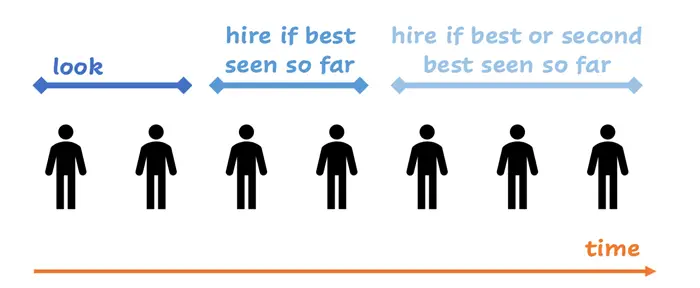
Bu nedenle sunulan ilk seçenekleri ne kadar beğenirseniz beğenin, karşılaştığınız tüm seçeneklerin ilk %37’sini — teknik olarak ilk %36,788’ini — koşulsuz olarak reddetmelisiniz.
Johannes Kepler Evlilik Sorununu Yüzde 37 Kuralı İle Nasıl Çözdü?
Matematik çevrelerinde bu bilmece birçok isimle anılır ve en çok “sekreter problemi” olarak bilinir. Ancak bu problemin gerçek kökeninin Johannes Kepler’e kadar uzandığı iyi belgelenmiştir
Kepler, bu konuyu 1611 ile 1613 yılları arasında, ilk eşinin ölümünün ardından ele aldı. Yeniden evlenmesi beklenen Kepler, doğru bir seçim yaptığından emin olmak istiyordu. Takip eden iki yıl boyunca yalnızca 11 potansiyel eş adayını titizlikle görüşüp araştırmakla kalmadı. Aynı zamanda her bir adayla ulaşabileceği “gerçek mutluluk” türünün rastgele dağıldığını varsayarak, yaptığı seçime bağlı olarak nasıl bir sonuçla karşılaşabileceğinin olasılıklarını da hesapladı.

Kepler, bu 11 kadınla sırayla tanışacağını varsaydı. İlk dört adayı sadece değerlendirmeyi, yani onlarla ne kadar mutlu olabileceğini anlamaya çalışmayı hedefledi. Onlara karşı ne hissederse hissetsin bu dört kadının hiçbirini seçmemeye karar verdi.
Bu ilk dört kişiden birinin en iyi eş olma ihtimali %36 civarındaydı (4/11). Ancak kalan yedi kişi arasında, bu ilk dördünden daha iyi birinin çıkma olasılığı %63’ten fazlaydı (7/11). Kepler’in stratejisi şuydu. Geriye kalan yedi kişiden, ilk dördüne göre daha iyi olduğunu düşündüğü ilk kadını seçerse, mutluluğunu en çok artırma şansını yakalayacaktı.
Bu problem sonraki yıllarda tekrar tekrar gündeme geldi ve işe alım, üniversite seçimi gibi pek çok duruma uyarlandı. Ayrıca, daha önce reddedilen seçeneklere geri dönmenin mümkün olduğu çeşitli varyasyonlara da uygulandı.
Peki Ama Neden %37?
Bu sorunun cevabını adım adım ilerleyerek bulalım. Diyelim ki bir grup aday arasından işe alacağınız kişiyi seçmeye çalışıyorsunuz. Eğer tek aday varsa, onu işe alın. İki aday olduğunda ise ne yaparsanız yapın doğru seçim yapma şansınız %50’dir.
Üçüncü bir aday eklendiğinde işler biraz karışır. Rastgele seçim yaparsanız, doğru adayı işe alma ihtimaliniz %33 ya da 1/3 olur. Peki, üç aday arasından en iyiyi seçme olasılığınızı artırabilir misiniz? Elbette artırabilirsiniz ve her şey ikinci adayla ilgilidir.
İlk adayla görüştüğünüzde elinizde hiçbir veri yoktur. İkinci adayla görüştüğünüzde ise onun ilkinden daha iyi mi yoksa daha kötü mü olduğunu bilirsiniz. Bu noktada onu işe almak ya da reddetmek seçeneğiniz vardır.
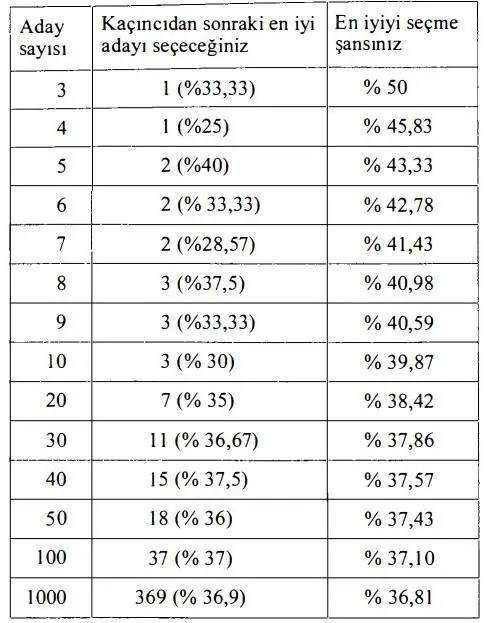
Şimdi tabloya göz atalım. Farkındaysanız sonuç giderek %37’e yaklaşmaktadır. Üstelik 100 ya da 1000 aday arasında da fazla bir fark yoktur. Aslına bakarsanız ne kadar çok adayı dikkate almanız gerekiyorsa, adayların ilk 1/ e kısmını tek taraflı olarak reddetmelisiniz (burada 1/ e = 0,36787944117…).
Eğer sizin için en iyi seçenek, ilk %36,788’lik (1/e’lik) bölümde yer alıyorsa, bu strateji gereği onu reddetmiş olursunuz. Yani onu seçme şansınız kalmaz. Buna karşılık, seçmediğiniz örneklem grubundan daha iyi bir seçeneğe rastlama ihtimaliniz %63,212’dir (1 – 1/e).
Öte yandan, ilk %36,788’lik kısmı eledikten sonra karşınıza çıkan adaylar arasında “şu ana kadar gördüklerinizin en iyisi” olanı seçtiğinizi varsayarsak, hâlâ bazı seçenekleri görememiş olacaksınız. En iyi adayın, bu hiç görmediğiniz grupta yer alma ihtimali yaklaşık %26,424’tür (1 – 2/e).
Sonuç olarak: %63,212 – %26,424 = %36,788 olur. Bu da, en iyi seçeneği bulma olasılığının 1/e olduğunu gösterir.
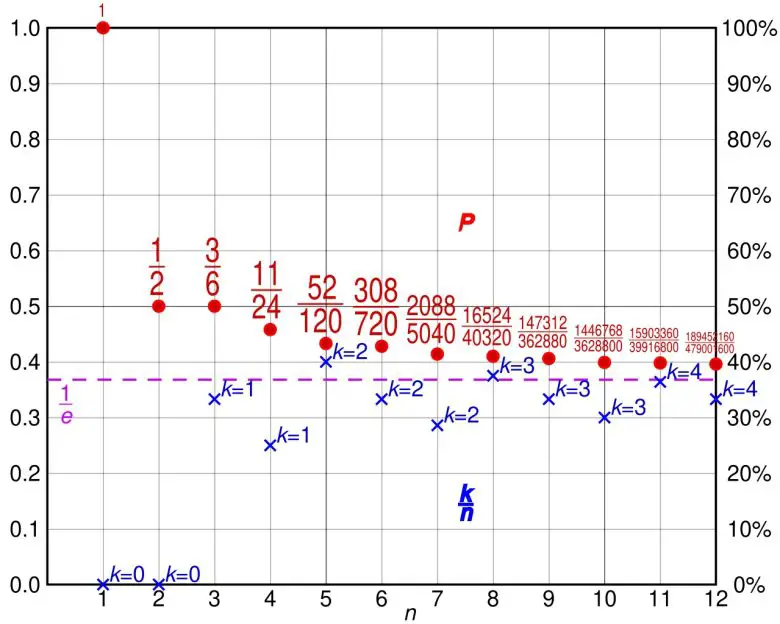
Burada “n” toplam seçenek sayısını, “k” ise örneklenip reddedilecek en uygun aday sayısını temsil eder.
Sonuç olarak
Hiçbir strateji en iyi kararı vereceğinizi garanti edemez. Ancak en iyiyi seçme olasılığınızı en üst düzeye çıkarmanın yolu sağlam matematiksel temellere dayanır. Kepler’in üzerinden 400 yıldan fazla zaman geçmesine rağmen, onun olasılık konusunda öğrendiği dersleri bugün de hayatımızdaki en büyük kararlara uygulayabiliriz.
Yazının devamında göz atmak isterseniz. Kepler Bir Şarap Fıçısının Hacmini Hesaplayarak Matematiğe Nasıl Bir Katkı Sağladı?
Kaynaklar ve ileri okumalar
- Thomas S. Ferguson. “Who Solved the Secretary Problem?.” Statist. Sci. 4 (3) 282 – 289, August, 1989. https://doi.org/10.1214/ss/1177012493
- Astronomer Johannes Kepler solved life’s hardest problem: marriage. Yayınlanma tarihi: 26 Temmuz 2023. Bağlantı: Astronomer Johannes Kepler solved life’s hardest problem: marriage/?
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





