Bir arkadaş ortamında, toplama işlemini hesap makinesinden daha hızlı yaparak çevrenizdekileri şaşırtmak ister misiniz? Muhtemelen istersiniz. O halde, size hızlı işlem yapmanızı sağlayacak basit bir yöntem gösterelim.

Öncelikle kâğıda 10 satır çizin ve her satırı 1’den 10’a kadar numaralandırın. Ardından arkadaşınızdan, 1 ile 20 arasında iki pozitif tam sayı düşünmesini isteyin. Bu iki sayıyı, kâğıtta 1. ve 2. satırların karşısına yazsın.
Sonrasında birkaç basit toplama işlemi yapması gerekiyor. 1. ve 2. satırdaki sayıları toplayıp sonucu 3. satıra yazacak. Daha sonra 2. ve 3. satırdaki sayıları toplayıp sonucu 4. satıra yazacak.
Bu işlemi aynı şekilde sürdürecek. Yani her seferinde üstteki iki satırın toplamı bir alt satıra yazılacak. En son olarak 8. ve 9. satırın toplamı, 10. satıra yazıldığında işlem tamamlanmış olacak. Aşağıda örnek bir kâğıt yer alıyor. Ancak önemli bir nokta var: Tüm bu işlemler yapılırken siz kâğıdı hiçbir şekilde görmeyeceksiniz.

İşlem tamamlandıktan sonra, arkadaşınızdan kâğıdı size göstermesini isteyin. Kâğıda şöyle bir göz attıktan sonra, yazılı olan tüm sayıların toplamını anında söyleyin. Örneğin, yukarıdaki örnekte bu toplam 671’dir. Bu sonucu bulmak için tüm sayıları tek tek toplamanız gerekmez.
Eğer arkadaşınızı daha da şaşırtmak isterseniz, ondan 10. satırdaki sayıyı hesap makinesiyle 9. satırdaki sayıya bölmesini isteyin. Ardından bölümün ilk üç basamağını bir yere not etmesini söyleyin. Siz de bu sonucu başka bir kâğıda yazıp üzerine kapatın.
Yapılacak bölme işlemi şu şekilde olacaktır: 257 ÷ 159. Bu işlemin sonucu yaklaşık 1,6163… olduğu için, ilk üç basamağı 1,61 olacaktır. Tahmininiz de tam olarak bu sayıya denk gelecektir.
Tüm Bunlar Nasıl Gerçekleşti
Hızlı toplama işlemini gerçekleştirmek için, 7. satırdaki sayıyı 11 ile çarpmanız yeterlidir. Örneğin, 61 × 11 = 671 eder. (11 ile hızlı çarpma yaparken, bir basamaklı iki sayının çarpımında, rakamların toplamını ortaya yazarak sonuca kolayca ulaşabilirsiniz: 6 ve 1’in toplamı 7 olduğundan, 61 × 11 = 671.)
Bu yöntemin neden işe yaradığını anlamak için aşağıdaki tabloyu incelemeniz gerekir. Tabloda, 1. ve 2. satırlardaki sayılar sırasıyla x ve y ile gösterilmiştir. Tabloda görebileceğiniz gibi, tüm sayıların toplamı 55x + 88y biçimindedir. Oysa 7. satırdaki sayı 5x + 8y’dir.
Bu da, toplam değerin 7. satırdaki değerin tam 11 katı olduğunu gösterir. Bu nedenle, 7. satırdaki sayıyı 11 ile çarpmak her zaman toplam sonucu verecektir.

Şimdi, ikinci tahminin nasıl yapıldığını açıklayalım. Bir kesri a/b ve başka bir kesri c/d olarak ele alalım ve a/b < c/d olsun. Eğer bu iki kesri, payları ve paydaları ayrı ayrı toplayarak yeni bir kesir oluşturursak, yani:
(a + c)/(b + d) elde edilen kesir, her zaman bu iki kesrin arasında bir değer alır.
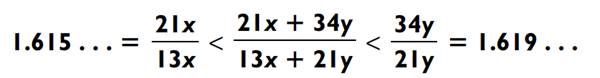
Dolayısıyla, 10. satırdaki sayıyı 9. satırdaki sayıya böldüğümüzde, sonuç bu iki değerin oranları arasında bir yerde olacaktır. Bu nedenle, bölüm yaklaşık olarak 1,61 ile başlar. Tahmin ettiğimiz üç basamaklı sayı da tam olarak budur.
Aslında, yukarıda anlatılan hızlı toplama oyununu daha uzun süre devam ettirirseniz, ardışık terimlerin oranı giderek, matematikte “altın oran” olarak bilinen değere yaklaşır. Altın oranın ne olduğunu anımsamayanlar için kısaca açıklayalım: Altın oran, yaklaşık 1,618 sayısına karşılık gelir. İki sayının oranı, daha büyük olanın, küçük olana oranı ile, her ikisinin toplamının büyük olana oranına eşit olduğunda elde edilir.

Matematik, bazen oyun gibi görünebilir; ama bu oyunların çoğu, sayılar dünyasında gizli kalmış şaşırtıcı düzenleri ortaya çıkarır.
Kaynak: Arthur Benjamin and Michael Shermer; The Mathemagician’s Guide to Lightning Calculation and Amazing Math Tricks; eISBN: 978-0-307-34746-6
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel