2000 yılında ABD’deki Clay Matematik Enstitüsü, yeni binyılın gelişini ödüllü yedi problemle kutladı. Matematikçileri neredeyse yarım yüzyıl boyunca uğraştırmış olan Poincaré varsayımı da bu problemler arasındaydı. Bu varsayımı birkaç yıl içinde Rus matematikçi Grigori Perelman çözdü. Asıl hikaye ise bu olaydan sonra başladı.

Çok az insan olağanüstü bir başarı elde edip sonra ortadan kaybolur. Bu nadir örneklerden biri, 1972’de İzlanda’nın Reykjavik kentinde düzenlenen Dünya Satranç Şampiyonası’nı kazanan Bobby Fischer’dır. 1975’te Fischer unvanını reddetti ve hem satrançtan hem de kamuoyundan tamamen çekildi.
Buna bir başka örnek ise matematiğin “taçsız kralı” Grigori Perelman’dır. Henri Poincaré’nin 1904’te ortaya attığı bu soruyu, 2002 yılında Grigori Perelman çözdü. Ancak onu asıl tanınır kılan, bu soruyu çözmesinin ötesinde, çözümden sonraki yaklaşımı oldu.
Perelman sadece problemi çözmekle kalmadı, aynı zamanda 33 sayfalık çözümünü internette, herkese açık bir bilimsel arşiv sitesinde yayımladı. Çözüm 2006 yılında resmen doğrulanınca Clay Matematik Enstitüsü, vaat ettiği 1 milyon dolarlık ödülü Perelman’a vermeye hazır hale geldi.

Matematiğin Nobel’i sayılan Fields Madalyası da Perelman’a verilmişti. Dünya bu gizemli adamı görmek için sabırsızlanıyordu. Ancak o bu ödülleri kabul etmedi. Dünya başarı peşinde koşarken, şu sözleriyle tarihe geçti: “Ben ünlü olmak istemiyorum. Sadece bir soruyu çözdüm ve bunun bu kadar büyütülmesi ilginç. Eğer yaptığım ispat doğruysa bu benim için yeterli ve tatmin edici.”
Grigori Perelman Kimdir?
Grigori “Grisha” Perelman, 13 Haziran 1966’da Sovyetler Birliği’nin Leningrad kentinde (bugünkü adıyla Rusya’nın Saint Petersburg kentinde) elektrik mühendisi bir baba ve matematikçi bir annenin çocuğu olarak dünyaya geldi. Perelman’ın annesi, onu ve küçük kız kardeşini büyütmek için yüksek lisans eğitiminden vazgeçti. Perelman matematik tutkusunu, ona matematiği öğreten annesine borçluydu.

Perelman’ın matematiksel yeteneği erken yaşlarda kendini belli etti. 16 yaşında Budapeşte’de düzenlenen Uluslararası Matematik Olimpiyatı’nda tam puan alarak altın madalya kazandı. Sonrasında Leningrad Devlet Üniversitesi Matematik ve Mekanik Fakültesi’ne girdi ve doktorasını tamamladı. Ardından başarılı bir akademik kariyer izledi.
New York Eyalet Üniversitesi’nde bir pozisyonu kabul etti, ancak New York’ta aradığını bulamadı. Sonrasında ABD’nin en iyi üniversitelerinden gelen teklifleri reddederek 1995’te Saint Petersburg’daki Steklov Enstitüsü’ne geri döndü. Ancak Berkeley’de geçirdiği iki yıllık süre boyunca Amerikalı matematikçi Richard Hamilton’dan çok şey öğrendi.
Bunu, çözümünü elektronik ortamda yayımladıktan sonra katıldığı davetlerde sık sık dile getirdi. Ancak Hamilton’dan beklediği ilgiyi görememek onun için bir hayal kırıklığıydı.
Poincaré Sanısı Çözüm Süreci Nasıl Gelişti?

Cebirsel topoloji, 19. yüzyılın sonlarında Henri Poincaré’nin çalışmasıyla başladı. Bu bize geometri ve topolojideki zor problemleri cebire dönüştürerek, karmaşık matematiksel nesneleri anlamanın bir yolunu sağladı.
Poincaré, topolojinin temelini atarken, aynı zamanda topolojinin en basit üç boyutlu nesnesinin, dört boyutlu bir yüzeyi belirlemek için yeterli araçlara sahip olup olmadığını düşünüyordu. Bu düşünce onu, tüm zamanların en meşhur sorularından birine yönlendirdi. Hiçbir belirleyici niteliği ( delik, kulp, büküm vs) olmayan bir üç-boyutlu uzay, mutlaka üç-boyutlu bir küre mi olmak zorundadır? İşte bu soru Poincare varsayımının temeliydi.
Poincare Varsayımı üzerine pek çok girişim oldu. Bill Thurston, 1970’lerin sonlarında üç boyutlu uzayları anlama konusunda muazzam ilerlemeler kaydetti. Onun fikirleri oldukça önemliydi. Teorilerini daha da geliştiren, özellikle de herhangi bir uzayın geometrik yapısını bulmaya çalışan güçlü bilgisayar programları üreten birçok parlak öğrencisi de vardı.
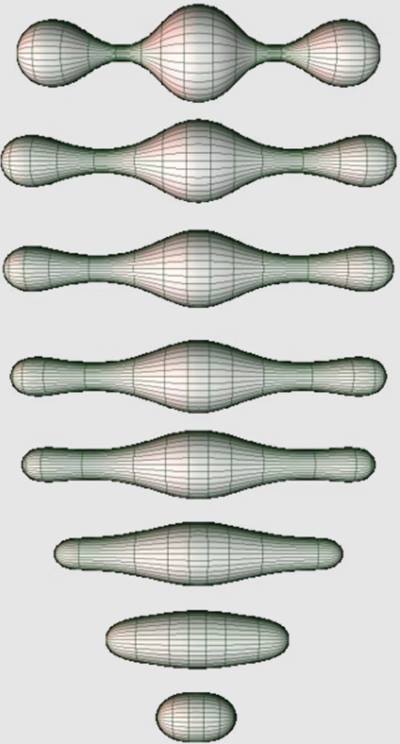
1982’de Richard Hamilton, geometrik analizde Ricci akışı adını verdiği yeni bir tekniği tanıtan güzel bir makale yayınladı. Kendisi aslında ısı akışı ile ilgileniyordu. Ancak uzayın geometrik şekli için de benzer bir akışın olması gerektiğini düşündü. Ricci akışı ve diğer benzer akışlar, hareketli ara yüzler, akışkanlar mekaniği ve bilgisayar grafikleri gibi alanlardaki uygulamalarla büyük bir araştırma alanı haline geldi.
Grigori Perelman Ödülü Neden Kabul Etmemişti?
Hamilton, bu olguyu tam olarak anlamak ve Thurston’un öngördüğü geometrik yapı ortaya çıkana kadar parçaların Ricci akışı altında nasıl gelişeceğini incelemek için yoğun şekilde çalıştı. İşte tam bu noktada Perelman devreye girdi.
Perelman çok genç yaşta bazı parlak sonuçlar elde etmişti ve o dönemde St. Petersburg’daki ünlü Steklov Enstitüsü’nde araştırmacı olarak çalışıyordu. 1990’ların başında üç yıllığına UC Berkeley’i ziyaret etmek üzere Miller Bursu’nu kazandı. Daha sonra ortadan kayboldu ve yıllar sonra Hamilton’un Ricci akışıyla ilgili çalışmasını tamamladığını duyurmak için yeniden ortaya çıktı.

Perelman başarıya sessiz sedasız ulaşmıştı. 2002’de konuyla ilgili 39 sayfalık ilk makalesini alışılmadık bir şekilde internete koydu ve özetini ABD’deki 12 matematikçiye e-postayla gönderdi. Ertesi yıl iki bölüm daha yayımladı. İspatı 2006’da matematik camiası tarafından tamamen kabul edildi.
2006’dan önce Perelman’ın Rusya’da çalıştığı Steklov Matematik Enstitüsü’nden istifa ettiği ve matematiği bıraktığı duyuruldu. Soranlara matematik camiasından emekli olduğunu ve artık kendisini profesyonel bir matematikçi olarak görmediğini söyledi.
Perelman’ın davranışlarında bilim idealini görmek mümkündü. O, sınanmak, tartışılmak, geçerliyse doğrulanmak ve değerinin bilinmesinden başka bir ödül istemiyordu. Bu tutumunun arka planında yaşadığı hayal kırıklıklarının etkisi de hissediliyordu. Çünkü Grigori Perelman, Hamilton ile işbirliği yapmak için iletişime geçse de yanıt alamamıştı. Yani Perelman’ın isyanına neden olan şey kendi sözleriyle “matematik dünyasından dışlanması”ydı.
Kaynaklar ve İleri Okumalar:
- Grigory Perelman, the maths genius who said no to $1m. Yayınlanma tarihi: 23 Mart 2010. Bağlantı: Grigory Perelman, the maths genius who said no to $1m;
- Özgür Narin; Perelman’ın İsyanı ve İspatı Üzerine Düşünceler; Bilim ve Gelecek sayı: 79; 2010
- The Mystery of Grigori Perelman. yayınlanma tarihi: 18 Mayıs 2019. Bağlantı: The Mystery of Grigori Perelman
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






