Dünyanın en ünlü bisiklet yarışının önceki kazananları şaşırtıcı derecede yaygın bir matematiksel ilişkiyi ortaya çıkıyor. Bu matematiksel ilişki Zipf yasası olarak isimlendiriyor.

Tour de France yani Fransa Bisiklet Turu, her yıl Fransa’da düzenlenen yol bisikleti çok etaplı yarış turudur ve şüphesiz ki dünyanın en ünlü bisiklet yarışıdır. Dünyanın dört bir yanındaki farklı ülkelerden gelen sporcular, ünlü sarı mayo için üç haftalık bir yarışta yarışırlar.
Bu yarışma Fransa’nın en önemli yıllık spor etkinliğidir ve derin kültürel köklere sahiptir. Ancak ülkelerin galibiyet sayısına baktığımızda da garip bir matematiksel ilişki karşımıza çıkar.
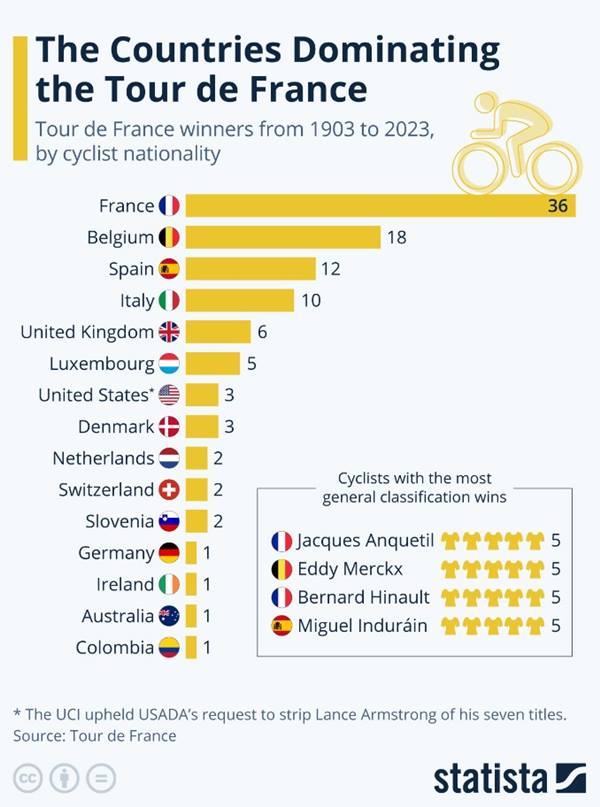
Yukarıda görebileceğiniz gibi, 18 galibiyetle ikinci sırada yer alan Belçika, Fransız bisikletçilerin elde ettiği 36 galibiyetin tam yarısı kadar başarı göstermiştir. En çok sarı mayoya sahip bir sonraki ülke olan İspanya, Fransa’nın galibiyet sayısının tam üçte biri (12) kadardır.
Listedeki bir sonraki ülke olan İtalya ise, Fransızların galibiyet sayısının dörtte birinden (10) sadece bir fazlasına sahiptir. Bu sayılar bize gizemli Zipf yasasını hatırlatır. Bu yasanın detaylarına geçmeden önce yukarıda gördüğünüz verileri bir grafik olarak aşağıda da inceleyebilirsiniz.
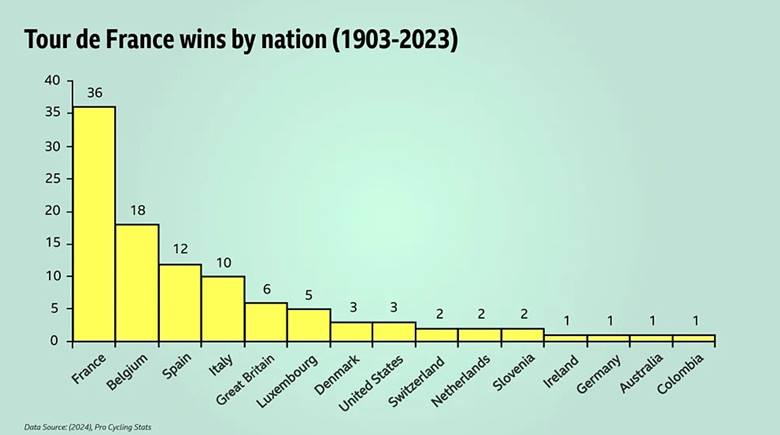
Zipf yasası nedir?
1940’larda, Harvardlı dilbilimci George Zipf, dilin özelliklerini incelemesinin ardından, Zipf Yasası olarak bilinen bir deneysel düzenlilik bulmuştur. (Bu tabii ki bir yasa değildir). Buna göre hangi dilde olursa olsun herhangi bir metinde geçen sözcükler, kullanılma sıklığına göre sıralandığında oluşan listede her zaman geçerli bir kural vardır.
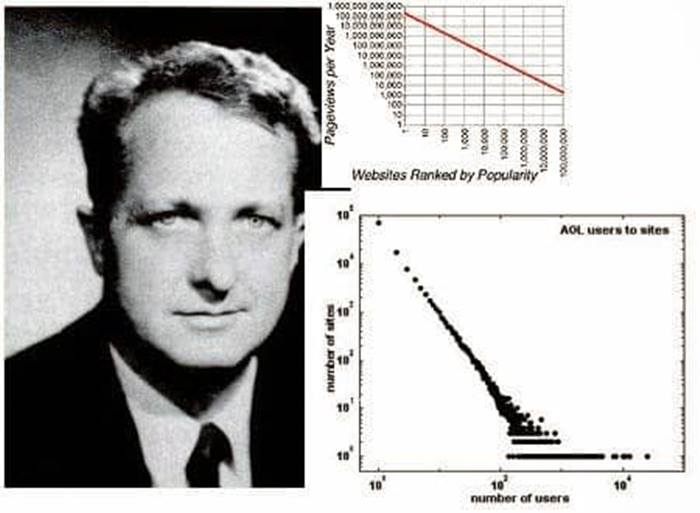
Zipf yasasına göre, bir dilde en çok görülen sözcük ikinci en çok görülen sözcükten aşağı yukarı iki kat, en sık rastlanan üçüncü sözcükten hemen hemen üç kat, yüzüncü sözcükten yüz kat vs. daha fazla kullanılır. Diyelim ki sadece 10 sözcükten oluşan bir dil var. Bu dille kaleme alınmış metinde en sık kullanılan sözcük 100 defa kullanılmış. Bu durumda en sık kullanılan kelimeden en az kullanılan kelimeye göre yapılan bir sıralama listesi aşağıdaki gibi olacaktır.
- 1. sözcük => 100/1 = 100
- 2. sözcük => 100/2 = 50
- 3. sözcük => 100/3 = 33,3
- 4. sözcük => 100/4 = 25
- 5. sözcük => 100/5 = 20
- 6. sözcük => 100/6 = 16,6
- 7. sözcük => 100/7 = 14,3
- 8. sözcük => 100/8 = 12,5
- 9. sözcük => 100/9 = 11,1
- 10. sözcük => 100/10= 10
Zipf yasası evrenseldir
Sıra-sıklık kuralı adı ile de bildiğimiz Zipf yasası evrenseldir. Sadece İngilizce için değil, görünüşe göre birçok başka dil için ve hatta yapay dil Esperanto için bile geçerlidir. Ve hatta insanlar yeni bir dil uydursa bile bu yasanın varlığı gözlemlenecektir.
Örnek vermek gerekirse İngilizcede “the” kelimesi yazılı her şeyin yaklaşık %6’sını oluşturur. Daha sonra da %3′ sıklıkla “of” kelimesi gelir. Bu ilk kelimenin yarısı kadardır. Bir sonraki “and” kelimesi de “the” kelimesinin yaklaşık 1/3’ü kadardır. Sonraki “a ” ise yaklaşık 1/4’ü kadardır ve bu biçimde devam etmektedir.
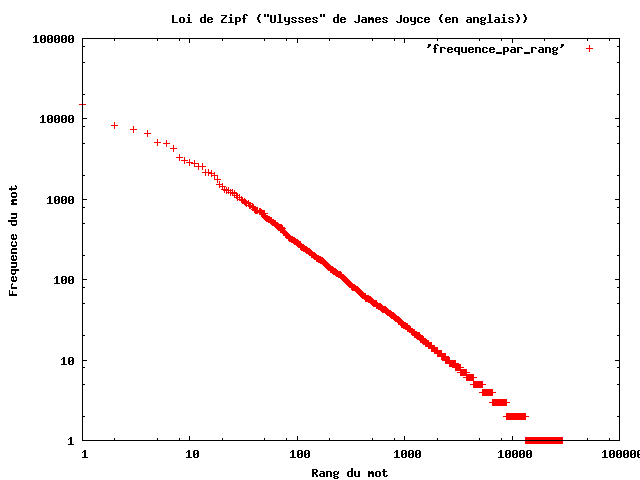
Ayrıca Tour de France örneğimizde gördüğümüz gibi, yalnızca bir metindeki kelimelerle sınırlı değildir. Zipf 1950′ de öldükten sonra bilim insanları bu yasanın kanıtlarına çok çeşitli yerlerde rastladılar. Örneğin araştırmacılar yazılan makalelerin sayısı, yerleşimlerin nüfus büyüklüğü, bağışıklıkla ilgili amino asit dizisi uzunlukları ve hatta aydaki kraterlerin çapları gibi son derece çeşitli senaryolarda karşımıza çıkıyordu.
Her seferinde her sınıflandırmadaki en büyük ya da en sık görünen öğe, ikinci büyük ya da sık rastlanan öğenin iki katıydı, üçüncü büyük ya da sık görünenin üç misliydi. Hatta Zipf bir keresinde Mozart, Chopin, gibi bestecilerin yaygın notaları araştırmış ve dağılımın Zipf yasasına uyduğunu bulmuştu.
Daha sonra araştırmacılar bu bulguları doğruladılar. Ayrıca tını, ses yüksekliği ve notaların uzunluğunda da Zipf dağılımına rastladılar. Üstelik Tour de France, Zipf yasasının geçerli olduğu bulunan tek spor bağlamı da değildir. Olimpiyat madalya tabloları da bu ilişkiyi bizlere yansıtır. Peki tüm bunların bir anlamı var mıdır?
Zipf yasası, kuvvet yasası adı verilen daha genel bir kuralın özel bir durumudur
Kaçınılmaz bir biçimde, kuramın aniden popülerlik kazanması, özellikle dilbilimciler arasında güçlü bir tepkiye yol açtı. Bir çok kişi tüm bunların bir anlamı olup olmadığını sorgulamaya başladı. Birbiri ile alakasız konunun ve karmaşık yapının kabaca da olsa bir yasaya uygun olmasının altında yatan nedene dair pek çok teori geliştirildi. Ancak tüm bu nedenlerin akla en uygun olanı matematik ile ilgili gibi gözüküyor.
Zipf yasası, kuvvet yasası adı verilen daha genel bir kuralın özel bir durumudur. Bu yasalarda bir değişken başka bir değişkenle ters orantılı olarak değişir. Ters orantılı olduğu için de bir değişkeni iki katına çıkarmak, diğerini yarıya indirmek veya üç katına çıkarmak, diğerini üçte bir olacak biçimde azaltmak anlamına gelir. Matematiksel olarak Zipf yasası şu denklemle ifade edilebilir: f(r) = K / rα . Zipf yasasının ortaya çıkması için α bir ya da bire yakın olmalıdır.
Güç yasalarının, çok çeşitli veri setlerini tanımladığı bulunmuştur. Ayrıca bu yasaların sistemler kendi kendine benzerlik gösterdiğinde ortaya çıktığı anlaşılmıştır. Bu ilgili özellikleri sergileyen sistemler, onları yakınlaştırdığımızda veya uzaklaştırdığımızda aynı (veya kabaca aynı) görünür.
Fraktal kıyı şeritleri, kendine benzerliğin sık alıntı yapılan bir örneğidir. Bir sahilin ana hatları göz önüne alındığında, tam olarak görüntülediğiniz ölçeğin boyutunu söylemek zordur. Yakınlaştırdığınızda, kıyı şeridinin yapıları benzer kalır. İnternet gibi ağlardan, kar taneleri gibi doğal olarak oluşan fiziksel olgulara ve eğrelti otları gibi biyolojik yapılara kadar birçok gerçek dünya olgusu, öz-benzer özellikler gösterir. Güç yasaları bu öz-benzerlik özelliğini matematiksel olarak yakalar.
Peki bu yılki yarış için bu ne anlama geldi?
Zipf yasasının Tour de France kazananları için tam olarak neden geçerli olması gerektiği açık değildir. Ayrıca Zipf dağılımını gerçek verilerin üzerine çizdiğinizde, uyum mükemmel değildir. Tour’u en çok kazanan Avrupa ülkeleri Fransa ve yakın komşuları Belçika, İspanya ve İtalya’ aşırı temsil edilmektedir.’dır ve aslında bu çok da şaşırtıcı değildir.
Tours de France’in ilk yıllarında katlımcıların çoğu Fransızlardan oluşuyordu. Örneğin, 1903’teki ilk yarışmaya katılan 60 bisikletçinin 49’u Fransız’dı. Ayrıca 1985’ten bu yana en ünlü spor müsabakasında hiçbir Fransız galip gelmediği için, yeterince temsil edilmeyen bazı ülkeler dağıtımda yer alma şansına sahip oldu. Bu arada hatırlatalım. Yakın zamanda sonuçlanan 2024 Tours de France’ı bir kere daha Fransa kazandı.
Kaynaklar ve ileri okumalar
- Xavier Gabaix, Zipf’s Law for Cities: An Explanation, The Quarterly Journal of Economics. Volume 114, Issue 3, August 1999, Pages 739–767, https://doi.org/10.1162/003355399556133
- Rusydiana, Aam & As-Salafiyah, Aisyah & Sanrego, Yulizar & Marlina, Lina. (2021). Fiqh on Finance: A Scientometric Analysis using Bibliometrix. Library Philosophy and Practice. 2021.
- Britannica, The Editors of Encyclopaedia. “Tour de France”. Encyclopedia Britannica, 21 Jul. 2024, https://www.britannica.com/sports/Tour-de-France. Accessed 24 July 2024.
- The mysterious maths at work in the Tour de France. Yayınlanma tarihi: 16 Temmuz 2023. Kaynak site: BBC. Bağlantı: The mysterious maths at work in the Tour de France
- Piantadosi ST. Zipf’s word frequency law in natural language: a critical review and future directions. Psychon Bull Rev. 2014 Oct;21(5):1112-30. doi: 10.3758/s13423-014-0585-6. PMID: 24664880; PMCID: PMC4176592.
- Yamada, Y. & Rêgo, Hênio & Stanley, H. & Yamamoto, K & Miyazima, Sasuke. (2018). The Zipf’s Distribution of the Number of Medals in 2016 Olympic Game in Rio DeJaneiro. International Journal of Humanities and Social Science. 8. 10.30845/ijhss.v8n10p8.
Matematiksel










