Carl Friedrich Gauss (1777–1855), tarihin en büyük matematikçilerinden biridir. Alman matematikçi ve fizikçi olarak birçok alanda önemli başarılara imza atmıştır. Bu yazıda ise onun, oldukça ilginç bir alan hesaplamasıyla ilgili katkısını ele alacağız.
Birazdan kısaca açıklayacağımız bu yöntem, İngilizcede “Gauss’s Shoelace Area Formula” olarak bilinir. “Shoelace”, Türkçede “ayakkabı bağcığı” anlamına gelir. Ayakkabı bağcığı formülü, diğer adıyla Gauss alan formülü düzlemde köşe noktaları verilen basit bir çokgenin alanını hesaplamaya yarayan matematiksel bir yöntemdir. Formül, adını koordinatlar arasında yapılan çapraz çarpımların bağcık bağlama hareketine benzemesinden alır.
Çoğu zaman Gauss’un adıyla anılsa da, formül ilk olarak Albrecht Ludwig Friedrich Meister (1724–1788) tarafından 1769’da tanımlanmıştır. Temelinde, Carl Friedrich Gauss ve C.G.J. Jacobi tarafından geliştirilen yamuk alanı formülü yer alır. Üçgene uygulanan hali ise, Green teoreminin özel bir durumu olarak değerlendirilmektedir.
Gauss Yöntemi İle Alan Hesabı Nasıl Yapılır?
Aşağıdaki şekilde bir dokuzgen görüyorsunuz. Köşe noktalarının koordinatları sırasıyla şu şekildedir: (2, 9), (3, 1), (5, 8), (4, 3), (9, 2), (13, 6), (6, 7), (9, 8) ve (6, 11). Bu çokgenin alanını hesaplarken Gauss alan formülünü kullanacağız.
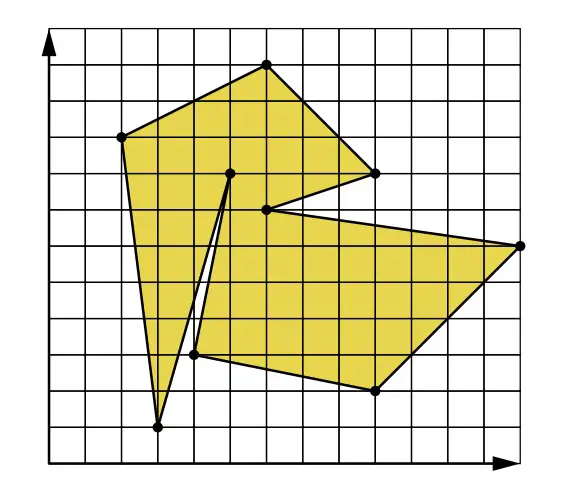
İlk olarak, kendinize bir başlangıç noktası seçin. (Hangi noktadan başladığınız önemli değildir.) Daha sonra, çokgenin çevresi boyunca saat yönünün tersine ilerleyin. Bu sırada karşılaştığınız köşe noktalarının koordinatlarını, x değerleri bir sütunda, y değerleri başka bir sütunda olacak şekilde listeleyin. Yukarıda verilen koordinatları esas alırsak, elde edeceğiniz liste aşağıda yer alıyor.

Şimdi, ilk olarak aşağıdaki görselde gösterildiği gibi, koordinatları soldan sağa doğru çaprazlama çarpın. Elde ettiğiniz çarpımları toplayın. Bu, birinci toplamınızı oluşturur. Daha sonra, aynı işlemi bu kez sağdan sola doğru yapın ve çıkan çarpımları yine toplayın. Bu da ikinci toplamınız olacak.
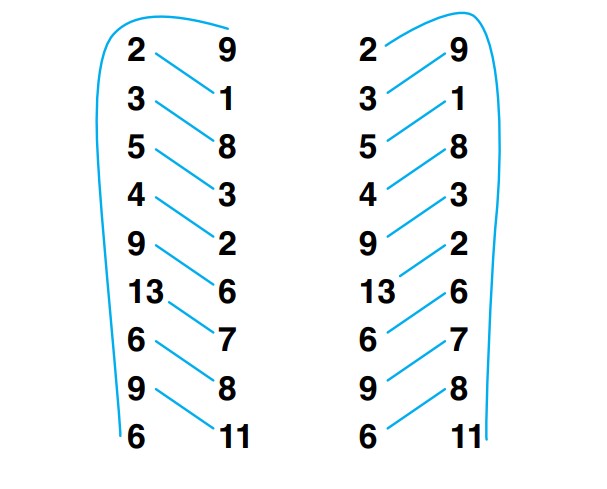
Şimdi bu iki toplamı birbirinden çıkarın. Elde ettiğiniz sonucu ikiye böldüğünüzde, çıkan değer çokgenin alanını verir. Aşağıda adım adım yapılan hesaplamaları görebilirsiniz.
- Toplam₁ = 2×1 + 3×8 + 5×3 + 4×2 + 9×6 + 13×7 + 6×8 + 9×11 + 6×9 = 395
- Toplam₂ = 9×3 + 1×5 + 8×4 + 3×9 + 2×13 + 6×6 + 7×9 + 8×6 + 11×2 = 286
- Fark = 395 − 286 = 109
- Alan = ½ × 109 = 54,5 birim²
Gauss Alan Hesabı İle İlgili Örneklere Göz Atalım
Şimdi, Gauss’un bize tanıttığı bu pratik alan hesaplama yöntemiyle, daha önce bildiğimiz bazı alanları kontrol edelim. İlk olarak, aşağıda bir üçgenin alanına bakalım.
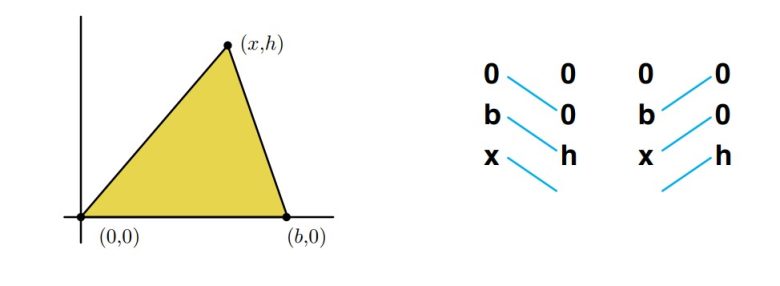
- Toplam₁ = 0 + b·h + 0 = b·h
- Toplam₂ = 0 + 0 + 0 = 0
- Fark = b·h
- Alan = ½ · b·h
Gördüğünüz gibi, Gauss yöntemi üçgenin alanını hesaplarken doğru sonucu verdi. Şimdi, taban uzunluğu b ve yüksekliği h olan bir paralelkenarın, koordinat düzlemine yerleştirilmiş haline bakalım.
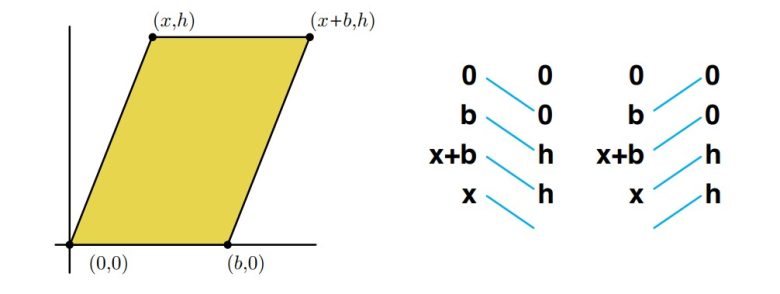
- Toplam₁ = 0·0 + b·h + (x + b)·h + x·0=
2bh + xh - Toplam₂ = 0·b + 0·(x + b) + h·x + h·0= h·x
- Fark = (2bh + xh) − xh = 2bh
- Alan = ½ × 2bh = bh
Gauss Yöntemi Neden İşe Yarıyor?
Bu sorunun cevabını, yani Gauss alan yönteminin ispatını bir örnek üzerinden yapalım. Bir köşesi orijinde, O = (0, 0) olan bir üçgen düşünün. Diğer iki köşesinin A = (x₁, y₁) ve B = (x₂, y₂) olduğunu varsayalım. Aşağıda gördüğünüz bu üçgenin alanı nedir?
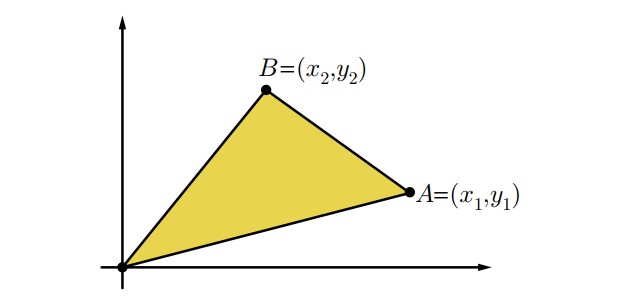
Bu üçgenin alanını hesaplamanın bildiğimiz bir yolu, onu bir dikdörtgenin içine yerleştirmektir. Ardından, dikdörtgenin alanından dışta kalan üç dik üçgenin alanlarını çıkarırız. Böylece geriye yalnızca hedef üçgenin alanı kalır. Bu durumda şekil aşağıdaki gibi görünür. Şimdi, sırasıyla A, B ve C alanlarını hesaplayalım.
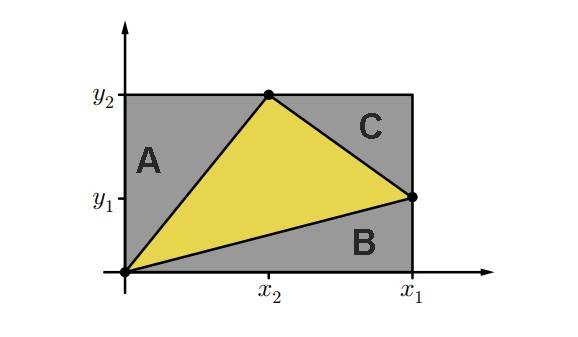
- A = ½·x₂·y₂
- B dik üçgeninin alanı: B = ½·x₁·y₁
- C dik üçgeninin alanı: C = ½·(x₁ − x₂)·(y₂ − y₁)
- Dikdörtgenin alanı ise: Alan = x₁·y₂
Bu durumda, dikdörtgenin alanından üç dik üçgenin alanını çıkardığımızda, sarı bölgenin alanı: Alan = ½·(x₁·y₂ − x₂·y₁) biçiminde olacaktır.. Şimdi, aynı sonucu Gauss alan yöntemiyle elde etmeye çalışalım.
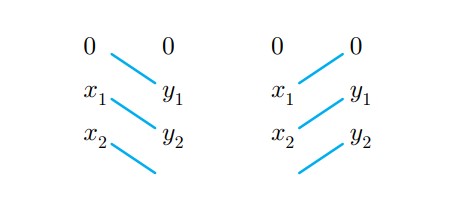
- Toplam₁ = 0 + x₁·y₂ + 0
- Toplam₂ = 0 + y₁·x₂ + 0
- Alan = ½·(x₁·y₂ − x₂·y₁)
Gördüğünüz gibi, sonuç önceki yöntemle aynı çıkıyor. Aslında, hangi üçgenle başlarsanız başlayın, bu formülle elde edeceğiniz alan değişmez. Ayakkabı bağcığı formülü, yalnızca basit çokgenlerde değil, kendiyle kesişen ya da üst üste binen çokgenlerde de geçerlidir. Bu da yöntemin güvenilirliğini ve genelliğini gösterir.
Kaynaklar ve ileri okumalar
- Gauss’s magic shoelace area formula and its calculus companion. Yayınlanma tarihi:10 Temmuz 2017; Bağlantı: https://www.youtube.com/watch?v=0KjG8Pg6LGk
- James Tanton; How Round Is a Cube? And Other Curious Mathematical Ponderings; LCCN 2019004260 | ISBN 9781470451158
- Gechlik, Jacob & Sedrakyan, Hayk. (2024). Gauss’s Area Formula for Irregular Shapes. Ohio Journal of School Mathematics. 97. 10.18061/ojsm.4172.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






