Galton Kutusu Kullanarak Geleceği Nasıl Görebilirsiniz?

Dünya çoğu zaman rastlantılarla ve öngörülemez olaylarla ilerliyormuş gibi görünür. Oysa matematiksel olasılık ve istatistik, bu karmaşanın altında işleyen birçok olgunun beklenmedik bir doğrulukla tahmin edilebildiğini gösterir. 19. yüzyılda İngiliz istatistikçi Sir Francis Galton da tasarladığı Galton tahtası ile, görünürdeki rastlantının ardında yatan bu matematiksel düzeni somut bir biçimde ortaya koymaya çalışmıştır.

Galton Kutusu Nedir?

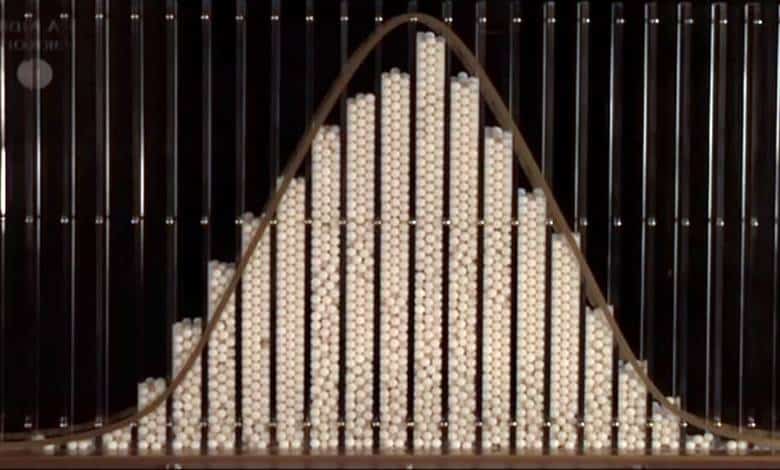
Galton tahtası, üçgen biçiminde dizilmiş çivilerden ya da pimlerden oluşur. Küçük metal bilyeler, üstteki bir açıklıktan içeri bırakılır. Bilyeler, langırt benzeri bir şekilde bir sıradaki pimden diğerine çarparak aşağı doğru ilerler ve en sonunda alttaki yuvalardan birine yerleşir. Tek tek her bir bilyenin sağa sola yaptığı zikzaklar tamamen rastgeleymiş gibi görünür.

Ancak Galton tahtasına çok sayıda bilye döküldüğünde şaşırtıcı bir düzen ortaya çıkar. Altta biriken bilyeler, her seferinde çan biçimli bir eğriye yaklaşık olarak uyan bir dağılım oluşturur. Ortaya en yakın yuvalarda bilyeler üst üste yığılırken, kenarlara doğru gidildikçe her bir yuvadaki bilye sayısı giderek azalır ve quincunx’un uçlarında sıfıra yaklaşır.

Bu örüntünün matematiksel bir açıklaması vardır. Tek bir bilyenin izlediği yol, birbirinden bağımsız yazı–tura atışlarının ardışık bir dizisi gibidir. Bilye her pime çarptığında ya sola ya da sağa seker ve uzaktan bakıldığında bu seçim tamamen rastgeleymiş gibi görünür. Sonuçta ortaya çıkan toplam, örneğin sağa gidişlerin sola gidişlere göre fazlalığı, bilyenin alttaki hangi yuvaya düşeceğini belirler.

1810 yılında Pierre-Simon Laplace tarafından kanıtlanan merkezi limit teoremine göre, bu tür rastgele süreçler, yani çok sayıda yazı–tura atışının toplamına karşılık gelen mekanizmalar, her zaman aynı olasılık dağılımına yol açar. Bu dağılım, normal dağılım ya da çan biçimli eğri olarak bilinir. Galton tahtası, Laplace’ın bu teoreminin görsel ve sezgisel bir gösteriminden başka bir şey değildir.

Bu Nasıl Gerçekleşiyor?

Bu kalıbı daha net görmek için, çok daha az sayıda pimin bulunduğu bir düzeneğe bakalım. Dört sıralı bir Galton kutusunda, bir topun en alta ulaşması için 16 farklı yol vardır. Aşağıda, bu olası yolların her birinin nasıl ortaya çıktığını inceleyerek, dağılımın arkasındaki mantığı görebiliriz.

Tahtanın tepesinden 160 top bıraktığımızı varsayalım. Dört sıra pinden oluşan bu düzende, her bir topun izleyebileceği toplam 16 farklı yol vardır. Bu nedenle, ilk bakışta her yolun yaklaşık on kez kullanılmasını bekleriz.

Ancak burada belirleyici olan, farklı yolların çoğu zaman aynı yuvada buluşmasıdır. Örneğin soldan ikinci yuvaya ulaşan dört ayrı yol vardır. Dolayısıyla bu yuvaya yaklaşık 40 topun düşmesi beklenir. Orta yuvaya ulaşan yol sayısı altıdır. Bu da yaklaşık 60 topun ortada toplanacağı anlamına gelir.

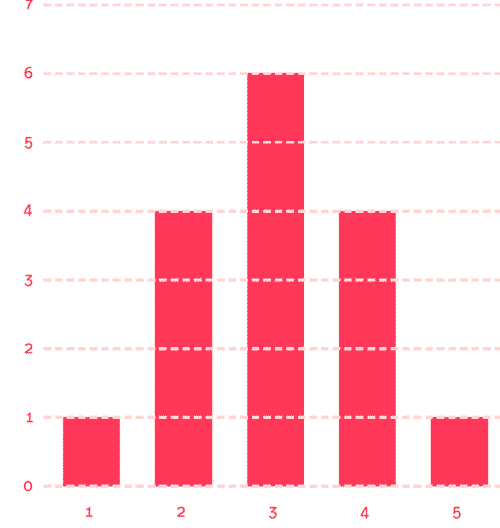
Tüm yuvalar için bu hesaplama yapıldığında, her yuvaya karşılık gelen yol sayıları 1, 4, 6, 4, 1 dizisini verir. Bu değerler bir grafiğe aktarıldığında, ortada yükselen ve kenarlara doğru simetrik biçimde azalan bir şekil ortaya çıkar.

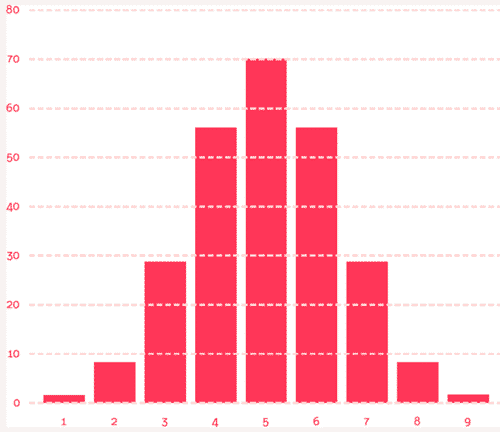
Bu alıştırmayı, daha uzun ve daha fazla yuvaya sahip bir Galton tahtası için yeniden yapalım. Örneğin 5 yerine 9 yuvalı bir düzenek kurduğunuzda, her yuvaya düşen yol sayıları 1, 8, 28, 56, 70, 56, 28, 8, 1 biçiminde ortaya çıkar. Bu değerleri grafiğe aktardığınızda çan eğrisine çok daha fazla benzeyen bir görünüm elde edersiniz.

Galton Kutusu Ne İşe Yarar?

Merkezi limit teoremi, 19. yüzyıl matematiğinin gerçek mucizelerinden biridir. Şunu düşünmek yeterlidir: Tek bir topun izlediği yol öngörülemezken, 1.000 topun davranışı son derece öngörülebilirdir.

Normal dağılıma götüren ilkeler, günlük hayatta karşılaştığımız pek çok olgunun arkasında sessizce çalışır. Aslında bu ilkeler, belirli sınırlar içinde “geleceği tahmin edebilmemizi” mümkün kılar. Örneğin evinizden şehir merkezine giden bir otobüse bindiğinizde, varış süresinin ne kadar olacağını nasıl kestirirsiniz?

Teorik olarak A noktası ile B noktası arasındaki tüm yolların uzunluğunu tek tek hesaplayıp her birini hız sınırına bölerek toplam süreyi bulmak mümkündür. Ancak pratikte bu anlamsız bir uğraştır. Yol boyunca karşılaşacağınız trafik ışıkları, duraklamalar ve beklenmedik aksaklıklar yolculuğu belirsiz sayıda kesintiye uğratır. İşte tam bu noktada normal dağılım devreye girer.

Yol üzerindeki trafik ışıkları, Galton tahtasındaki iğneler gibi davranır. Bazı araçların hiç durmadan geçmesine izin verirken, bazılarını durdurur. Ancak tıpkı bir topun her seferinde aynı yöne sapmasının çok düşük bir olasılık olması gibi, bir yolculuk boyunca her ışıkta durmanız ya da hiçbirinde durmamanız da pek olası değildir.

Bu yolculuğu birçok kez tekrarladığınızda tablo netleşir. Zamanla, yolda harcanan süreler Galton tahtasında biriken toplar gibi bir dağılım oluşturur. Çoğu yolculuk ortalama bir sürede tamamlanır. Çok kısa ya da çok uzun süren yolculuklar ise nadir görülür.

Bu nedenle çevrimiçi haritalar, tek tek tüm ayrıntıları bilmeden, tipik bir yolculuğun ne kadar süreceğini doğru biçimde tahmin eder.. Tahmini varış sürelerinin çoğu zaman isabetli olmasının arkasında yatan temel neden de budur.

Yazının devamında göz atmak isterseniz: Abraham de Moivre: Ölüm Tarihini Hesaplayan Bilim İnsanı

---

Kaynaklar ve ileri okumalar:

• Carney, Mark & Varcoe, Ben. (2022). Universal Statistical Simulator. 10.48550/arXiv.2202.01735.
• Galton Board; Bağlantı: https://mathworld.wolfram.com/GaltonBoard.html

---

Size Bir Mesajımız Var!

Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel