Bir gezegenin geometrik yapısını belirlemenin yollarından biri, uzaya araç gönderip yüzeyini dışarıdan görüntülemektir. Şu ana kadar yalnızca sınırlı sayıda insan bu tür görüntüleri doğrudan elde etme fırsatı bulmuştur. Elde edilen veriler, gezegenin küresel bir şekle sahip olduğunu göstermektedir

Uzay teknolojilerine başvurmadan da, üzerinde yaşanılan yüzeyin geometrik özelliklerini belirlemek mümkündür. Bu amaçla başvurulacak matematiksel yöntemlerden biri Euler karakteristiğidir. Bu kavram, pek çok temel kurala adını vermiş olan matematikçi Leonhard Euler’in çalışmalarına dayanmaktadır.
Dünya’nın küresel yapısı, uzay çağından ya da 15. yüzyıl denizcilerinden çok daha önce bilinmekteydi. Bu bilgiye Euler karakteristiğiyle ulaşılmadı. Ancak bu yöntem, yalnızca yer yüzeyinden yapılan gözlemlerle bir yüzeyin topolojik yapısının belirlenebileceğini göstermesi açısından dikkate değerdir. Bu yaklaşım, Dünya’nın yapısını anlamada teorik ama güçlü bir araç sunar.
Euler Karakteristiği Nedir?
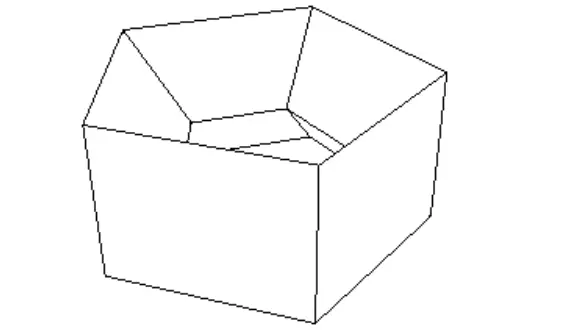
Tıpkı yaş gibi, Euler karakteristiği de yalnızca bir sayıdır. İki boyutlu yüzeyler için — bir kutu, plaj topu ya da gezegen gibi — bu sayı, şeklin köşe sayısından (V) kenar sayısı (E) çıkarılıp yüz sayısı (F) eklenerek elde edilir: V − E + F
Basit bir örnekle başlayalım. Bir küpün 8 köşesi, 12 kenarı ve 6 yüzü vardır. Dolayısıyla: 8 − 12 + 6 = 2
Bu, küpün Euler karakteristiğidir.
Peki, küre için durum nedir? Küre üzerinde doğal köşe ve kenar yoktur; bunları çizerek tanımlarız. Bir yaklaşım, küre üzerine ekvator ve meridyenler çizmektir. Elinizde bir küre yoksa, bir greyfurtun etrafına lastik bantlar dolayarak benzer bir yapı oluşturabilirsiniz.

Bu çizgiler, yüzeyi parçalara ayırarak köşe, kenar ve yüzlerin sayısını belirlemeyi mümkün kılar. Sayılar farklılık gösterse de doğru bir şekilde uygulandığında Euler karakteristiği her zaman 2 çıkar. Bu, yüzeyin kapalı ve deliksiz — yani topolojik olarak bir küre — olduğunu gösterir.
Yapılan düzenlemede, lastik bantların kesişim noktalarında 6 köşe, aralarında 12 kenar, ve bu kenarların oluşturduğu 8 yüz vardır. Buradan 6 − 12 + 8 = 2 sonucunu elde ederiz. Bu da kürenin Euler karakteristiğini verir. Lastik bantlar küreye farklı biçimlerde yerleştirilebilir. Bu durumda köşe, kenar ve yüz sayıları değişse bile, eğer yüzeyin temel yapısı korunuyorsa, sonuç değişmez.
Bu, Euler karakteristiğinin yapılan seçimlerden bağımsız bir özellik olduğunu gösterir. Sayılar değişse de, yüzey küresel kaldığı sürece, çizim ne kadar değişirse değişsin, Euler karakteristiği yine 2 olarak kalır.
Euler karakteristiği bir topolojik sabittir.
Euler karakteristiği, bir yüzeyin topolojik yapısını tanımlamada güçlü bir araçtır. Kapalı ve deliksiz bir yüzeyle karşılaştığında — ister küre olsun, ister küp ya da tetrahedron — her zaman aynı sonucu verir: 2. Çünkü bu yüzeyler topolojik olarak aynıdır.
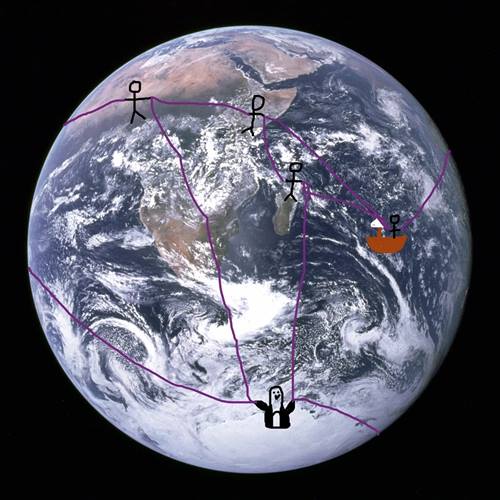
Dünya’nın topolojisini test etmek için uzaya çıkmana gerek yok. Birkaç kişi ve uzun iplerle bu testi doğrudan uygulayabilirsin. Herkes yeryüzünde bir noktada durur, ipleri birbirine bağlar. Ardından:
- Kaç kişi olduğunu (V),
- Kaç ip parçası kullandığını (E),
- Kaç kapalı bölge oluşturduğunu (F) say.
- Sonra V − E + F işlemini yap. Sonuç 2 çıkarsa, bulunduğun yüzeyin topolojisi bir küreye eşdeğerdir.
Eğer farklı bir sayı bulursan, ya yanlış saydın ya da farklı bir yüzeydesin. Bu durumda, yüzeyin yönlenebilirliğini ve sınır sayısını da göz önünde bulundurman gerekir. Bu bilgilerle, yüzeyin yalnızca neye benzediğini değil, topolojik türünü de açıkça belirleyebilirsin.
Yönlenebilirlik Ve Sınır Sayısı Sorunu
Yönlenebilirlik, yüzeyin topolojik sınıflandırmasında belirleyici bir özelliktir. En bilinen yönlenemez yüzeylerden biri Möbius şerididir. Bu tür yüzeylerde, bir noktadan harekete başlanıp aynı noktaya dönüldüğünde, başlangıçtaki yön tersine döner.. Yönlenebilir yüzeylerde ise bu durum ortaya çıkmaz. Yüzeyin iç ve dışı ayırt edilebilir ve başlangıç noktasına dönüşte yön korunur.

Bir diğer belirleyici özellik, yüzeyin sınır sayısıdır. Yüzeyin bir kenarının bulunup bulunmadığı, topolojik yapıyı doğrudan etkiler. Eğer bir kenar varsa ve bu kenardan dışarı çıkmak mümkünse, yüzey kapalı değildir. Sınır bir adet olabileceği gibi birden fazla da olur.. Böyle bir durumda yüzey, pul biçiminde ya da şekil olarak sekize benzeyen bir yapıda olabilir.
Euler karakteristiği, yönlenebilirlik ve sınır sayısı birlikte değerlendirildiğinde, yüzeyin hangi topolojik türde olduğu netleşir. Euler karakteristiği 2 ise, yüzey küreyle topolojik olarak aynıdır. Her sınır parçası Euler karakteristiğini bir azaltır. Sonuç 1 olduğunda, bu durum delik açılmış bir küreyi, yani düzlemdeki bir çokgenle eşdeğer bir yapıyı gösterir. Eğer sonuç 0 çıkarsa, yüzey torus ya da sınır içeren bir pul biçiminde olabilir.
Sonuç Olarak

Topolojiyi belirledikten sonra, sıradaki adım geometridir. Yüzeyin küreyle topolojik olarak aynı olması, şeklin gerçekten bir küre olduğu anlamına gelmez. Euler karakteristiği burada artık bilgi vermez. Bu aşamada, Eratosthenes gibi düşünmek gerekir: Gölgelere bak, ışığın geliş açısını ölç, yüzeyin belirli bir noktada ne kadar eğimli olduğunu hesapla. Geometriyi anlamanın yolu budur.
Kaynaklar ve ileri okumalar
An Impractical, Ahistorical, Mathematically Elegant Way to Figure out Earth Is a Sphere. Kaynak site: Scientific American. Yayınlanma tarihi 28 Ocak 2016. : Bağlantı: An Impractical, Ahistorical, Mathematically Elegant Way to Figure out Earth Is a Sphere
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel