19. yüzyılın sonlarında cereyan etmiş Dreyfus olayı bir siyasi skandaldır. Skandal, Fransız Yahudi topçu subayı Yüzbaşı Alfred Dreyfus’un (1859-1935) tutuklanmasıyla sonuçlanmış ve bu nedenle de onun adını almıştır. Dreyfus Olayı, casusluk, aldatma, gücün kötüye kullanılması, savaşan siyasi gruplar hakkında karışık bir hikayedir. Ancak bizi ilgilendiren aynı zamanda kötü bir matematik hikayesi olmasıdır.

Dreyfus Olayı Nasıl Başladı?
Olay 1894’te, Paris’teki Alman Büyükelçiliği’nde bulunan bir Fransız casusun, çöp sepetinde yırtık bir mektup bulması ile başladı. Bu kâğıt parçası istihbaratın başında bulunan Albay Jean Sandherr’e ulaştığında Fransız kamuoyunda küçük bir kıyamet kopacaktı. Sandherr bir Yahudi karşıtı olmasıyla ünlüydü ve davanın seyrini değiştirecek kişi olacaktı.
Bu mektubun Fransız ordusuna ait bilgiler içerdiği anlaşıldı. Bunun devamında da Fransız Ordusunda bulunan bir Alman casusu için cadı avı başladı. Soruşturmalar sonucunda kuşku duyulan dört subay arasından Alfred Dreyfus’da yer alıyordu. “Dikkat çekecek kadar güçlü bir belleğe sahip olması”, “fazla kültürlü olması”, çok iyi Almanca bilmesi gibi özellikleri nedeniyle Dreyfus casusluk için güçlü bir adaydı.

Dreyfus aleyhine tek doğrudan kanıt ise el yazısı ile yazdığı bir not idi. Bu nottaki yazı ile mektuptaki yazının karşılaştırılması gerekmektedir. Önce tarafsız bir bilirkişiden nottaki yazı ile Dreyfus’un el yazısının karşılaştırması istendi. Ancak bu kişi bir benzerlik görememişti. Bunun için savcılık aslında el yazısı analizi konusunda uzman olmayan Alphonse Bertillon‘u bilirkişi olarak mahkemeye çağıracaktı. Soruşturmanın başında da Sandherr yer alıyordu.

Dreyfus Neden Ve Nasıl Suçlandı?
Bertillon, adli adli tıp için ilk bilimsel yöntemleri geliştiren kişi olarak Fransa ve Batı dünyasında ünlüydü. Kullandığı yöntem temelde suçluları ölçmekti. Parmak izi veya DNA testi gibi karşılaştırma araçlarının henüz bilinmediği zamanlarda adli soruşturmalarda bu en tutarlı yöntem olarak kabul edilmekteydi. Ancak Bertillon’un el yazısı analizi konusunda bir uzmanlığı yoktu. Aynı zaman da ne yazık ki sağlam bir matematik kavrayışına da sahip değildi.
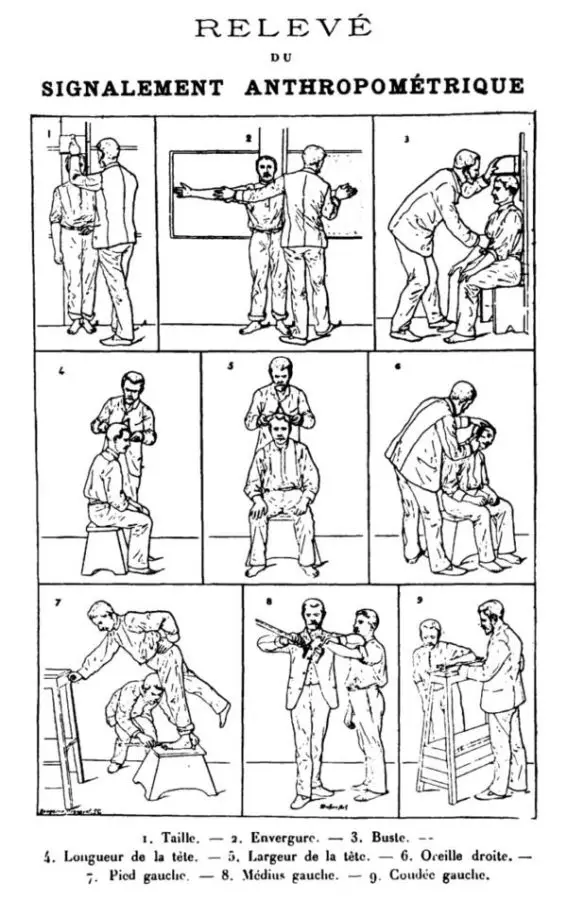
Bu 1893 çizelgesinde Bertillon, doğru ölçümlerin nasıl yapılacağını anlatıyor.
Bertillon, notta tekrarlanan çok heceli sözcüklerin kalem vuruşlarındaki bir dizi benzerliğe dayanan karmaşık bir matematiksel analiz yaptı ve Dreyfus’un kendi el yazısını sanki başkası yapıyormuş gibi taklit ederek el yazısını gizlediğini kanıtlamaya çalıştı.
Argümanı yedi kişilik bir jüriyi ikna etmeye ya da en azından şaşırtmaya yeterliydi. Sonucunda 1894 Ekim Alfred Dreyfus casusluk şüphesiyle tutuklandı. Sonrasında Dreyfus Fransız Ginesi’nin kuzeyinde yer alan Şeytan Adası’na ömür boyu sürgüne gönderilecekti. Bertillon’un itibarı da Dreyfus olayına karışması nedeniyle lekelenecekti.

Bertillon tek bir nota bakarak sanığın suçlu olduğuna karar verdi. Şüphelinin bilinen el yazısını nottakiyle kısaca karşılaştırdıktan sonra, kendinden emin bir şekilde bu Yahudi yüzbaşının kesinlikle düşmanla işbirliği yaptığını beyan etti.
Dreyfus Davası Émile Zola’nın İsyanı Sonucunda Tekrardan Dikkatleri Çekecekti
Aslında Dreyfus’un belge ile ilişkilendirilmesinin başka nedenleri de vardı. Öncelikle Dreyfus zengin bir Yahudi ailesine mensuptu. Ordu içerisinde durdurulamayan bir yükselişi vardı. Kimilerine göre bir profilin Fransız çıkarlarına hizmet etmesi mümkün olamazdı. Bu nedenle bu olay kısa süre içinde ört pas edilmek istense de süreç istenilen biçimde gelişmedi.
Dreyfus Davası kapanacağı yerde giderek büyüdü. Onun suçsuzluğuna inan kişilerin sayısı günden güne artmaktaydı. Basında da yargılama süreci ile ilgili eleştiriler yer almaya başlamıştı. Aynı zamanda, dürüst bir subay olarak tanınan Georges Picquart’ın yaptığı bazı araştırmalar sonucu gerçek suçlunun Marie Charles Ferdinand Walsin Esterhazy isimli başka bir subay olduğu ortaya çıkarmıştı.

Ancak Esterhazy 10 Ocak 1898’de yargıç önüne çıksa da, üç dakika içerisinde oy birliğiyle suçsuz bulunacaktı. Çünkü ordunun onuru ve ulusun çıkarı söz konusuydu. Bunun üzerine, gerçekleri kamufle etmek için harekete geçen ırkçı gazetecilere karşı Emile Zola, Le Figaro gazetesinde adalet ve gerçek yolunda hareket eden Picquart’a övgü niteliğinde “Gerçek Yürüyor, Onu Hiçbir Şey Durduramaz” yazısını yazdı. Kendisi Dreyfus’u aslında hiç tanımazdı. Onun sorunu adalet sorunuydu.
Zola kaleme aldıklarını yayımlatacak gazete bulamayınca mücadelesini broşürler aracılığıyla sürdürdü. Hükümetin tüm gerçekliği kapatma faaliyetlerinin yanı sıra Picquart’ın da cezalandırılması Zola’yı sonrasında da “Cumhurbaşkanı Felix Faure’a Açık Mektup” makalesini yazmaya sevk etti. Gazetecilik tarihinde eşine az rastlanır bir meydan okumayla hükümet, parlamento ve tüm milliyetçileri karşısına alarak adalet istedi.

Émile Zola ‘nın sık sık kullanılan “Suçluyorum- J’Accuse” mottosu bu mektupta yer alıyordu. Onun bu sözleri insanları harekete geçirecekti. Bu yazının devamında da Zola hükümete hakaretten önce ağır para cezasına ardından da hapis cezasına çarptırılacaktı.
Dreyfus Olayı Nasıl Sona Erdi?
Beş yıl sonra, Dreyfus yeniden yargılanma hakkını kazandı. Bu süreçte bir önceki dava dosyası da gözden geçirilmekteydi. Bunun için görevlendirilen kişi ise dünyaca ünlü matematikçi Henri Poincare olacaktı. Bu iş için Poincare’ye iki Fransa’nın önemli iki matematikçisi daha yardım etti. Sonucunda Poincaré, Bertillon’un hesaplamasındaki hatayı hemen fark edecekti. ( Göz atmak isterseniz: Henri Poincaré Matematik Sayesinde Adaleti Nasıl Sağladı?)

Cour de Cassation’ın talebi üzerine hazırlanan titiz bir raporda, Poincare ve arkadaşları Dreyfus’un yazısının analizinde basit olasılık hataları yapıldığını ispatladılar. Bu ikinci duruşmadan bir yıl sonra Dreyfus serbest bırakılacaktı. Devamında Fransız Ordusu’nda binbaşılığa terfi etti ve Birinci Dünya Savaşı’nda ülkesine hizmet etmeye devam etti. Esterhazy isimli, asıl suçlu olan kişi ise suçunu itiraf etti.
Dreyfus olayı tek bir dava değil, birbiriyle bağlantılı bir dizi askeri, hukuk ve ceza davasıdır. Bu nedenle size bu yazıda aktardıklarımız davaların kısa bir özetidir. Ayrıca Dreyfus olayı, bir askeri görevlinin haksız yere suçlanması ve ordudan atılmasından ibaret de değildir. Dreyfus Davası, ülkedeki iktidar ilişkilerinin ortaya konulduğu, insanlık onurunun hiçe sayıldığı bir olaydır. Bu olay aynı zamanda bize kötü matematik ve kötü mantığın, tarihin akışını değiştirme potansiyeli taşıdığını da anımsatır.
Kaynaklar ve ileri okumalar:
- Math and the Dreyfus affair; Bağlantı: https://uh.edu/engines/epi2933.htm
- Baysan, Gül. (2002). Dreyfus Davası : Gerçek ve Adalet Savaşçısı Zola. Hacettepe Üniversitesi Edebiyat Fakültesi Dergisi (Journal of Faculty of Letters). 19. 181-195.
- Man who invented the mug shot: The ground-breaking work of Alphonse Bertillon. Yayınlanma tarihi:22 Şubat 2015; Bağlantı: https://www.independent.co.uk/
- Kaye, David. (2006). Revisiting ‘Dreyfus’: A More Complete Account of a Trial by Mathematics. Minnesota law review. 91.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










