David Hilbert’in “sonsuz otel paradoksu” (Hilbert’s Hotel), sonsuzluk kavramının sezgilere aykırı doğasını gözler önüne seren çarpıcı bir düşünce deneyidir.

Bir sonraki yüz yılı ilgilendiren problemleri tahmin etmek, özel bir teknik zeka ve kendine güven gerektirir. Neyse ki, bu iki özellik de Alman matematikçi David Hilbert’te fazlasıyla mevcuttu. 1900’da Paris’teki Uluslararası Matematik Kongresi’nde, David Hilbert, gelecek yıllarda matematikçilerin zihinlerini meşgul edeceğine inandığı 23 soruyu büyük bir özgüvenle sundu.
Bu, onun ne kadar ileri görüşlü bir matematikçi olduğunun açık bir kanıtıydı. Aynı zamanda, matematik dünyasına büyük bir meydan okuma yapıyor ve gelecekte matematiksel araştırmaların yönünü belirleyecek bir çerçeve çiziyordu.
Ancak kendisinin matematiğe tek katkısı bu değildi. Hilbert, matematiği daha kesin ve tutarlı bir temele oturtmak için aksiyomatik yöntemi geliştirdi. Öklidyen geometriyi sistematik bir şekilde yeniden yapılandırarak, aksiyomların önemini vurguladı. Ayrıca, sayı teorisi, fonksiyonel analiz, cebir ve mantık alanlarında da büyük keşifler yaptı. Ancak tüm bunların ötesinde kendisi en çok Sonsuzluk Oteli paradoksu ile anımsanır.
Hilbert’in Sonsuzluk Oteli Paradoksu Nedir?
Diyelim ki bir otel yöneticisisiniz ve oteliniz tamamen dolu. Elbette bu harika bir durumdur, ancak daha fazla misafiri içeri almak her zaman cazip gelir. Gerçek hayatta bu, TripAdvisor’da kötü yorumlar almak anlamına gelir. Fakat matematik dünyasında bu sorun olmaz.
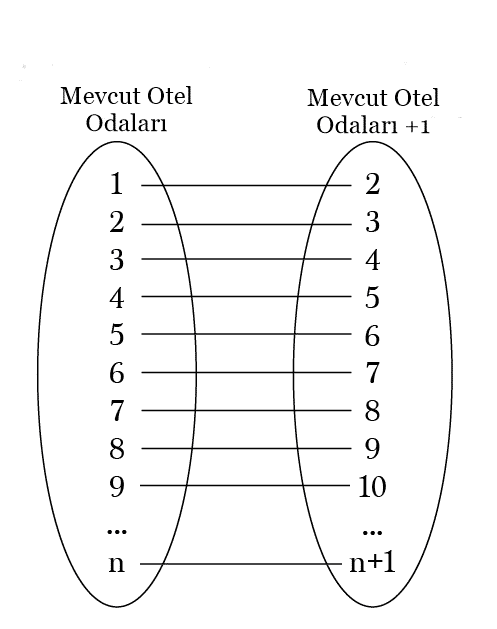
Diyelim ki otelinizde tüm odalar dolu ve yeni bir misafir geliyor. Ne yaparsınız? Cevabı basit. 1 numaralı odadaki kişiden 2 numaralı odaya geçmesini, 2 numaradakinden 3’e geçmesini, 3’tekinden 4’e geçmesini istersiniz ve bu böyle devam eder. Eğer yalnızca sonlu sayıda oda olsaydı, son odadaki kişinin gidecek yeri olmazdı. Ama burada sonsuz oda olduğu için herkes yeni bir odaya taşınır. Bu durumda da ilk oda boşalmış olur.
Bu yöntemle sonlu sayıda yeni misafiri otele almak da mümkündür. Diyelim ki nnn tane yeni misafir geliyor. Her mevcut misafire, oda numaralarına nnn eklenmiş yeni bir odaya geçmeleri söylenir. Örneğin, eğer 5 yeni misafir geldiyse, şu anda 10 numaralı odada kalan kişi 15 numaralı odaya geçer. Bu şekilde ilk 5 oda boşalır ve yeni gelen misafirler buralara yerleştirilir.
Ama işler burada bitmiyor. Farz edelim ki otelin önünde düzenli bir sırayla bekleyen sonsuz sayıda yeni misafir var. Bu durumda ne yapılır? Mevcut her misafiri, oda numarasının iki katı olan odaya taşırsınız. Örneğin, 7 numaralı odada kalan kişi 14 numaralı odaya geçer. Bu hamleden sonra yalnızca çift numaralı odalar dolu olur: 2, 4, 6, 8, 10… gibi. Tüm tek numaralı odalar ise boş kalır.
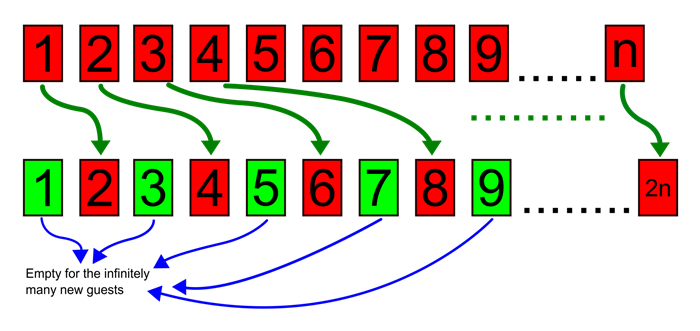
Böylece, yeni gelen ilk misafiri 1 numaralı odaya, ikinciyi 3 numaralı odaya, üçüncüyü 5 numaralı odaya yerleştirerek tüm yeni misafirleri de mutlu edebilirsiniz.
Hilbert Sonsuzluk Otelinde Neler Oluyor?
Bu daha başlangıç. Diyelim ki sonsuz sayıda otobüs geldi ve her otobüs sonsuz sayıda yeni yolcu taşıyor. Kolaylık olması açısından, otobüsler 1, 2, 3, … diye numaralandırılmış olsun ve her otobüsteki koltuklar da aynı şekilde 1, 2, 3, … olarak sıralansın.
İlk olarak, mevcut misafirleri daha önce yaptığımız gibi, oda numaralarının iki katına taşıyoruz. Yani, 12 numaralı odadaki misafir 24 numaralı odaya geçiyor. Bu hamle sayesinde tüm tek sayılı odalar boş kalıyor.

Şimdi, otobüs 1’in 1 numaralı koltuğundaki yolcuyu 3 numaralı odaya, 2 numaralı koltuktaki yolcuyu 3² = 9 numaralı odaya, 3 numaralı koltuktaki yolcuyu 3³ = 27 numaralı odaya yerleştiriyoruz. Genel olarak, otobüs 1’deki n. koltuktaki yolcu, 3n numaralı odaya taşınıyor. Çünkü 3’ün bütün kuvvetleri tek sayıdır ve bu nedenle bu odalar boş kalmıştır.
Peki, 2 numaralı otobüsle gelen misafirler nereye yerleştirilecek? Bu kez 5 sayısını kullanıyoruz (çünkü 3’ten sonra gelen asal sayı). Otobüs 2’nin n. koltuk numarasındaki yolcusunu, 5n numaralı odaya koyuyoruz. Örneğin, 1 numaralı koltuktaki yolcu 5 numaralı odaya, 2 numaralı koltuktaki 25 numaralı odaya, 3 numaralı ise 125 numaralı odaya yerleşiyor. Bu düzeni sürdürerek her otobüs için bir asal sayı seçiyoruz.
Bu odaların hepsi gerçekten boş mu kalacak? Cevap: Evet, kesinlikle boş kalacak. Yeni gelen misafirlerin yerleştirildiği tüm oda numaraları asal sayıların kuvvetleridir. Bu da bizi matematikte “aritmetiğin temel teoremi” olarak bilinen olağanüstü bir sonuca götürür.
Bu teoreme göre, her doğal sayı yalnızca bir şekilde asal sayıların çarpımı şeklinde yazılır. Bu da şu anlama gelir: Bir oda numarası belirli bir asal sayının kuvvetiyse, başka bir asal sayının kuvveti olamaz. Örneğin, otobüs 1’deki 5 numaralı yolcu 243 numaralı odaya yerleştirilmişse (çünkü 3⁵ = 243), bu odada başka hiçbir yolcu olamaz. Çünkü 243 sadece 3’ün kuvvetidir (3⁵), 5’in ya da başka bir asalın kuvveti olamaz.
Sonsuzluk Otelinde Her Zaman Bir Oda Var mı?
Yukarıda verdiğimiz sayı oyunları sonsuzluk fikrinin ne kadar esnek ve şaşırtıcı olabileceğini gösterse de, bu örneklerin ardından “O halde her zaman herkese yer vardır” diye düşünmeniz doğal. Ancak cevabımız hayır. Çünkü David Hilbert’in bu düşünce deneyindeki asıl amacı, sonsuzluk kavramının sezgilerimize aykırı doğasını gözler önüne sermektir.
Sonsuzluğun en tuhaf yanlarından biri, aslında büyüklük kavramıyla ilgilidir. “Sonsuzun büyüğü mü olur?” diye sorabilirsiniz, ama evet, olur. 19. yüzyılın sonlarında Alman matematikçi Georg Cantor, tüm sonsuzlukların eşit olmadığını ve bazı sonsuzlukların diğerlerinden daha büyük olduğunu ispatladı.

Örneğin, doğal sayıların kümesi (1, 2, 3, …) sonsuzdur. Ama reel sayılar kümesi — özellikle 0 ile 1 arasındaki tüm ondalıklı sayılar — çok daha büyük bir sonsuzluk içerir. Cantor bunu “sayılabilir” ve “sayılmayan” sonsuzluklar arasındaki farkla açıklamıştır. Doğal sayılar gibi elemanlarını tek tek numaralandırabileceğimiz kümeler sayılabilir sonsuzluk içerirken, reel sayılar gibi üyeleri arasında bu şekilde birebir eşleme yapamayacağımız kümeler sayılmayan sonsuzluk barındırır.
Sonuç Olarak
Hilbert’in oteli bize sayılabilir sonsuzluklarla neler yapılabileceğini gösterir. Ama Cantor’un gösterdiği gibi, bu oyunların sınırları vardır. Bazı sonsuzluklar o kadar büyüktür ki, sonsuz odalı bir otel bile onları ağırlayamaz.
Kaynaklar ve ileri okumalar için:
- Hilbert’s paradox of the Grand Hotel; Bağlantı: https://en.wikipedia.org/
- Hilbert’s hotel; yayınlanma tarihi: 13 Şubat 2017; bağlantı: https://plus.maths.org/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel