Bazı bilimsel keşifler önemlidir çünkü yeni bir gerçeği ortaya çıkarırlar. Bazı buluşlar ise uzun süre ayrı olduğu düşünülen iki kavramın aslında aynı şey olduğunu gösterirler. Curry-Howard bağıntısı (Curry-Howard correspondence) da benzer bir şey yapar. Birbirinden ayrı olduğunu sandığımız bilgisayar bilimi ve matematiksel mantığı birbirine bağlar.

Curry-Howard izomorfizmi olarak da bilinen bu yaklaşım, matematiksel ispatlarla bilgisayar programları arasında bire bir ilişki kurar. Basitçe ifade edersek, Curry-Howard bağıntısı bilgisayar bilimindeki iki kavramı (tipler ve programlar), mantıktaki iki kavrama (önermeler ve ispatlar) denk kabul eder.
Bu bağıntının önemli sonuçlarından biri, genellikle kişisel bir zanaat gibi görülen programlamayı matematik düzeyine yükseltmesidir. Artık bir program yazmak yalnızca “kodlama” değildir; aynı zamanda bir teoremi ispatlama eylemine dönüşür.
Peki Curry-Howard Bağıntısı Nasıl Ortaya Çıktı?
Bağıntıya adını veren araştırmacılar, keşfi birbirinden bağımsız olarak yaptı. 1934’te matematikçi ve mantıkçı Haskell Curry, matematikteki fonksiyonlarla mantıktaki “eğer–ise” biçimindeki önermeler arasında benzerlik fark etti. Curry’nin gözlemlerinden esinlenen mantıkçı William Alvin Howard ise, 1969’da hesaplama ile mantık arasında bir bağlantı kurdu.
Howard’a göre bilgisayar programı çalıştırmak, bir mantık ispatını adım adım basitleştirmeye benzer. Programda her satır işlenir ve sonunda tek bir sonuç elde edilir. Mantıksal ispatta da başlangıçta karmaşık ifadeler vardır; adımlar basitleştirilir, gereksiz kısımlar çıkarılır ve sonunda net bir sonuç ortaya çıkar.
Her ne kadar yukarıda Curry-Howard yazışmasının genel anlamını aktarmış olsak da bu tanım onu anlamak için yeterli değildir. Bu yüzden bilgisayar bilimcilerin tip teorisi (type theory) adını verdiği bir fenomeni anlamamız gerekiyor.
Tip Teorisi Nedir?
Ünlü bir paradoks şöyledir: Bir köyde bir berber vardır. Bu berber, sadece kendini tıraş etmeyen erkekleri tıraş eder. Peki, berber kendini tıraş eder mi? Eğer ederse kuralı bozar, çünkü kendini tıraş edenleri tıraş etmemelidir. Eğer etmezse yine kuralı bozar, çünkü kendini tıraş etmeyenleri tıraş etmelidir.

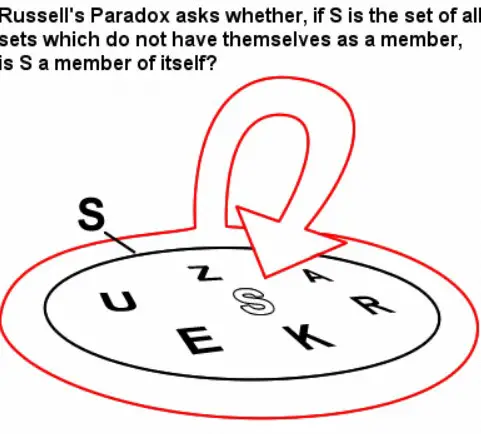
Bu çelişki, Bertrand Russell’ın matematiğin temellerini araştırırken bulduğu paradoksun basit bir örneğidir. Kısaca, “kendisini içermeyen tüm kümeleri içeren bir küme” tanımlamaya çalıştığınızda, işin içinden çıkılamaz bir çelişki ortaya çıkar.
Russell bu paradokstan kurtulmak için “tipler” fikrini ortaya attı. Tipleri basitçe kategoriler gibi düşünebilirsiniz. Her tipin içinde belli nesneler vardır. Örneğin “Doğal Sayılar” tipi (Nat) 1, 2, 3 gibi sayıları içerir.
Fonksiyonlar da tipler arasında çalışır. Mesela tip A’dan bir değer alıp tip B’den bir değer döndüren fonksiyon, A → B şeklinde yazılır. Paradoksu çözmenin yolu, tipleri bir sıralama içine koymaktır. Böylece her tip sadece kendisinden daha düşük seviyedeki tipleri içerebilir ve kendi kendini içeremez.
Tip teorisinde bir önermeyi kanıtlamak, alıştığımızdan biraz farklıdır. Örneğin “8 çifttir” demek için, 8’in belli bir tipe ait olduğunu göstermemiz gerekir. Bu tipin kuralı 2’ye bölünebilir olmaktır. 8’in 2’ye bölünebildiğini gösterdiğimizde, onun gerçekten de o tipin bir üyesi olduğunu kanıtlamış oluruz.
Curry ve Howard, tiplerle mantıktaki önermelerin aslında aynı şey olduğunu gösterdi. Bir fonksiyonun bir tipe ait olması, ilgili önermenin doğru olduğunu kanıtlamak gibidir. Örneğin A’dan B’ye giden bir fonksiyon (A → B), “Eğer A doğruysa, o zaman B de doğrudur” demektir. Yani programlama diliyle mantık dili farklı görünür ama aynı anlamı taşır.
Curry-Howard Bağıntısı Neden Önemli?
Bu bağ ilk bakışta soyut görünse de, hem matematikte hem de bilgisayar biliminde çalışma biçimini kökten değiştirdi ve pek çok pratik uygulama doğurdu. Bilgisayar biliminde programların gerçekten doğru çalıştığını matematiksel olarak kanıtlamanın yolunu açtı.
Programcılar, istedikleri davranışları mantıksal önermelerle tanımlayıp, programın bu kurallara uyduğunu gösterebiliyor. Aynı zamanda, güçlü işlevsel programlama dillerinin tasarlanmasına sağlam bir temel sağladı.
Matematikte ise bu fikir, Coq ve Lean gibi “ispat asistanları”nın gelişmesine yol açtı. Bu yazılımlar, matematiksel ispatları adım adım bilgisayarın kontrol etmesine imkân tanıyor. Örneğin Coq’ta her ispat adımı bir program gibi işleniyor ve tip denetimiyle doğruluğu sınanıyor. Lean sayesinde de matematikçiler teoremleri ve ispatları bilgisayarların denetleyebileceği kesin bir dile dökebiliyor. Araştırmacılar hâlâ bu bağlantının yeni boyutlarını keşfediyor.
Kaynaklar ve İleri Okumalar
- The Deep Link Equating Math Proofs and Computer Programs ; Yayınlanma tarihi: 11 Kasım 2023. Kaynak site: Quanta Magazine. Bağlantı: The Deep Link Equating Math Proofs and Computer Programs | Quanta Magazine
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





