
Yolu istatistik bilimine düşmüş herkesin bir şekilde aşina olduğu isim olan Kolmogorov, yirminci yüzyılın en büyük matematikçilerinden biridir. Matematiksel istatistik alanına yapmış olduğu katkıların yanında; çok çeşitli bilimsel alanda da çalışmaları vardır. Bu durum O’nu, geçtiğimiz yüzyılın en önemli bilim insanlarından biri yapar.
Kısaca Andrey Kolmogorov
Rusya’nın Tambov kentinde doğan ve aristokrat bir aileye sahip olan Andrei Nikolaevich Kolmogorov ( 25 Nisan 1903 – 20 Ekim 1987) erken yaşta annesini kaybedince teyzesi tarafından büyütülmüştü. 1910’da teyzesi onu evlat edindi ve 1920’de liseden mezun olduğu Moskova’ya taşındılar. Aynı yıl daha sonra Kolmogorov, Moskova Devlet Üniversitesi’nde ve aynı zamanda Mendeleev Moskova Kimya ve Teknoloji Enstitüsü’nde çalışmaya başladı. 1925’te mezun olduktan sonra Kolmogorov, araştırma öğrencisi olarak üniversitede kalış süresini dört yıl daha uzatmış ve 1929 yılında doktorasını tamamlamıştır.
Kolmogorov’un hayatında yine bu yılın ayrı bir önemi vardır. Çünkü kendisi gibi bir matematikçi olan Pavel Sergeevich Aleksandrov (1896 – 1982) ile başlayan dostlukları, hayatının en önemli olaylarından birine dönüşmüştür. Birlikte uzun tatiller yapan bu iki matematikçi, 1935’te Moskova’nın dışında küçük bir köy olan Komarovka’da bir ev satın almışlar ve bu ev, diğer ünlü matematikçileri de ağırlamıştır.

1931’de Moskova Üniversitesi’nde Profesör olan Kolmogorov, matematik ve fen bilimleri alanındaki yoğun çalışmalarının yanı sıra, zamanının çoğunu Sovyetler Birliği’ndeki ortaokullarda matematik öğretimini geliştirmeye ve matematikte üstün yetenekli öğrenciler için özel okullar oluşturmaya ayırmıştır. Anna Dmitriyevna Egorov ile 1942 yılında evlenmiştir. Özellikle Puşkin’in eserlerinin geri planındaki anlam arayışının ve biçimsel yapısının peşine düşen Kolmogorov, Rus şiiri üzerine yapılan çalışmalara da oldukça ilgilidir.
Bilime Sunduğu Katkılar
İlk Yıllar: 1903-1933
Kolmogorov ilk zamanlardan itibaren Rus tarihi ve matematikle ilgilenir. Matematikte Kolmogorov’un ele aldığı ilk konular arasında küme teorisi, projektif geometri ve analitik fonksiyonlar teorisi vardır. 1921-1922 yılları arasında ilk bağımsız matematiksel başarısını Fourier (Fransız Matematikçi, 1768 -1830) Serileri üzerinde yaptığı çalışmalar sonucu elde eder (Fourier-Lebesgue serisinin keyfi olarak yavaşça azalan Fourier katsayıları ile varlığı) ve Nikolai Luzin‘in (Rus Matematikçi, 1883 – 1950) öğrencisi olur.
Kolmogorov matematiksel mantıkla ilgilenmeye başlar ve 1925’te bu alanda sonraki çalışmalar için sürekli bir kaynak haline gelen “dışlanmış orta yasa (the law of the excluded middle)” teorisi üzerine bir makale yayınlar. Bu yayın, matematiksel mantık üzerine (çok önemli) yeni sonuçlar içeren ilk Sovyet yayını ve sezgisel mantık üzerine dünyadaki ilk sistematik araştırmadır.
Kolmogorov büyük ölçüde A. Heyting‘in (Hollandalı Matematikçi ve Mantıkçı, 1898 – 1980) sezgisel akıl yürütme biçimlendirmesini öngörerek klasik ve sezgisel matematik arasında daha kesin bir ilişki kurmuştur. Böylece bir mantıksal teoriyi diğerine “yerleştirmek” için bir operasyon tanımlamıştır. Tarihsel olarak bu ilk operasyon -şimdi Kolmogorov operasyonu olarak adlandırılıyor – klasik mantığın içine sezgisel mantık ilkelerini yerleştirmek için dışlanmış orta yasanın uygulanmasının kendi içinde bir çelişkiye yol açmayacağını kanıtlamıştır. 1932’de Kolmogorov, sezgisel mantık üzerine ikinci bir makale yayınlamış ve burada ilk kez (mantık için) sezgiselliğin felsefi amaçlarından arındırılmış bir anlambilim bakış açısı önermiştir. Bu makale, sezgisel mantığı yapıcı mantık olarak ele almayı mümkün kılmıştır.
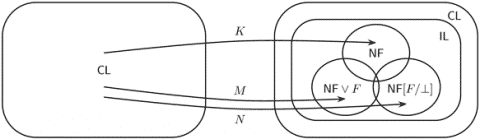
Olasılık teorisine olan ilgisi 1924 yılında başlamıştır. Bu alandaki ilk adımları Aleksandr Yakovlevich Khinchin (Rus Matematikçi, 1894 – 1959) ile birlikte gerçekleştirmiştir. 1928’de “güçlü büyük sayılar yasasının” korunması için gerekli ve yeterli koşulları bulmayı başarmış ve bağımsız rasgele değişkenlerin toplamları için yinelenmiş logaritma yasasını, çok genel koşullar altında, toplamlar üzerinde kanıtlamıştır.
1929’da “genel ölçü teorisi ve olasılıklar hesabını” yani olasılık teorisi için gerçek bir değişkenin fonksiyonlarının teorisine ve ölçü teorisine dayanan aksiyom sisteminin ilk taslağını ortaya koymuştur. Böyle bir teori ilk olarak 1909’da E. Borel (Fransız Matematikçi, 1871 – 1956) tarafından önerilmişti, 1923’te Lomnicki (Polonyalı Matematikçi, 1881 – 1941) tarafından daha da geliştirilmiş ve Kolmogorov’un 1933’teki çözümlemesiyle çok başarılı bir şekilde son şeklini almıştır.
Olasılık teorisi üzerine çok önemli çalışmalar zaten vardır; ancak 1933’te yayınlanan “Olasılık Hesabının Temelleri (Foundations of the Calculus of Probabilities)”kitabıyla konunun formülasyonunu göstermiştir. Bu kitap, matematiğin bir dalı olarak olasılık teorisinin geliştirilmesinde sadece yeni bir aşama belirlememiş; aynı zamanda Kolmogorov’un 1931 yılında yayınladığı makalesinin konusu olan “rastgele süreçler teorisinin” temelini de anlatmıştır.

Sonsuz boyutlu dağılımlar üzerine temel teoremler, rastgele fonksiyonlar teorisinin ve rastgele değişkenlerin dizilerinin titiz bir şekilde inşası için mantıksal temeller ilk olarak bu kitapta formüle edilmiştir. Geçtiğimiz yüzyılda Kolmogorov’un olasılık ve istatistik teorisine yaptığı katkılar, bu alanın en önde gelen temsilcisi olarak kabul edilmesini sağlamaktadır.
1931’de Kolmogorov’un modern Markov (Rus Matematikçi, 1856 – 1922) süreçleri teorisinin temellerini attığı “Olasılık Teorisinde Analitik Yöntemler (Analytical Methods in Probability Theory)” makalesi yayınlanır. Markov süreçlerinde yalnızca mevcut durum, gelecekteki durumların olasılığıyla herhangi bir etkiye sahiptir; bu nedenle ‘durumların’ geçmiş olayların “hafızasını” tutmadıkları söylenir. Kolmogorov, bir Markov sürecinde geçiş olasılıklarını karakterize etmek için bir çift işlev icat etmiş ve bunların “anlık ortalama” ve “anlık varyans” dediği şeye karşılık geldiklerini göstermiştir.
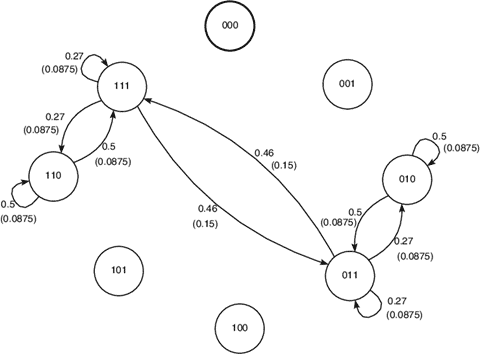
Bu fonksiyonları kullanarak bir durumdan diğerine geçiş olasılıklarını belirlemek için bir dizi kısmi diferansiyel denklem yazdığından bu denklemler olasılık teorisinin fizik, kimya, biyoloji ve inşaat mühendisliği üzerine uygulanmasına tamamen yeni bir yaklaşım sağlamıştır.
Bir hipotezin geçerliliğini test etmek amacıyla veri kümesinin sahip olduğu gerçek dağılımları hakkında bilgi edinmek için Kolmogorov, matematiksel istatistiğin temel problemlerinden birini ele almış ve rastgele gözlenen dağılımın ampirik dağılım fonksiyonunu kullanarak elde ettiği ünlü kriterini (Kolmogorov’un testi) sunduğu bir makale yayınlamıştır. Bu yayın aslında istatistik araştırmalarımızda karşımıza normallik sınamaları olarak çıkan Kolmogorov – Smirnov Testi diye duyduğumuz çalışmanın temelidir. Genel olarak Kolmogorov’un olasılık ve istatistik hakkındaki fikirleri, sayısız teorik gelişmeye ve günümüz fizik bilimlerinde sayısız uygulamaya yol açmıştır.
Gençlik Yılları: 1929-1940

1930-1940 yılları arasında Kolmogorov, felsefe ve matematik tarihini etkileyen başta olasılık teorisi olmak üzere; projektif geometri, matematiksel istatistik, gerçek bir değişkenin fonksiyonlarının teorisi, topoloji, harmonik analiz, matematiksel mantık, matematiksel biyoloji üzerine altmıştan fazla makale yayınlar.
ABD’li topolog James Waddell Alexander II (1888 – 1971) ile eş zamanlı fakat ondan bağımsız olarak Kolmogorov, “kohomoloji” (cebirsel topoloji kavramıdır) kavramını keşfetmiş ve “kohomolojik işlemler teorisini” kurmuştur. Kolmogorov ve kurmuş olduğu okulunun topoloji, sıradan diferansiyel denklemler teorisi, göksel mekanik ve dinamik sistemler teorisi arasındaki derin bağlantılar üzerine çalışmaları mevcuttur.
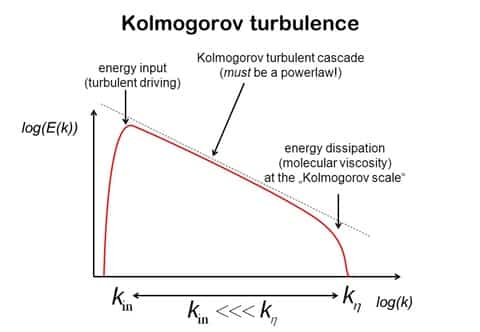
Otuzlu yılların sonunda, Kolmogorov dikkatini türbülans mekaniğine çevirir. Çalışmalarıyla türbülans teorisine -fonksiyon uzaylarının ölçü teorisinde uygulanması üzerine- matematiksel form kazandırır. 1941’de bu konuya ait iki makalesinde büyük fiziksel sezgiyle -özellikle Geoffrey Ingram Taylor (İngiliz Fizikçi, 1886 – 1975) tarafından daha önceki deneysel çalışmalarda bulduğu akışkanların ve gazların türbülanslı hareketini, küçük ölçekli bileşenlerinin yapısı üzerine tanımladığı- özlü matematiksel formları ortaya koymuştur.
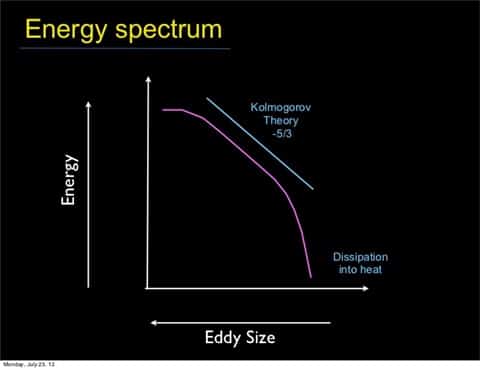
Bu hipotezler, yaygın olarak uygulanabilir birçok niteliksel sonuca – örneğin bir jet uçağının ardından meydana gelen türbülans içinde neler olabilir? – işaret eder. Kolmogorov ayrıca teorilerine dayanarak niceliksel tahminler de yapmıştır ve bunlar daha sonra deneylerle doğrulanmıştır. Kolmogorov’un türbülans teorisine 1941’deki katkıları, türbülans teorisinin uzun ve bitmemiş tarihinin belki de en önemli çalışmaları olmuştur.
Orta Yaşlar: 1940-1960

O ve öğrencileri bitkilerin etkileşiminin geometrisi hakkında yayınlar hazırlamış ve ayrıca “doğum ile ölüm” süreçlerini irdeleyerek genetik bilimine önemli katkılarda bulunmuşlardır. Durağan zaman serilerinin düzeltilmesi ve öngörülmesi teorisi genellikle Norbert Wiener (ABD’li Matematikçi, 1894 – 1964) adıyla ilişkilendirilir; ancak aslında İkinci Dünya Savaşı sırasında Wiener ve Kolmogorov tarafından eşzamanlı olarak geliştirilmiştir.
Savaş sonrası dönemde Kolmogorov yeniden türbülans mekaniği çalışmalarına dönmüş; daha önce keşfettiği ve deneysel olarak doğrulanan yasalarda küçük iyileştirmeler yapmıştır. Klasik mekanik, ergodik teori (fizik ve termodinamik kuramıdır), fonksiyon teorisi, bilgi teorisi ve algoritma teorisinin geniş yelpazesindeki çalışmaları bu döneme aittir.
Tamamen bağlantısız alanlar arasında bağlantılar bulmayı başarmış ve pek çok konuda az sayıda; ancak oldukça temel makaleler yayınlamıştır. Dinamik sistemler üzerine yaptığı çalışmalarda iki dönem ayırt edilebilir. İlki, 1953-1954 arasında H. Poincare (Fransız Matematikçi, 1854 – 1912) tarafından elli yıl önce güneş etrafındaki gezegenlerin hareketi üzerine yaptığı çalışmada tanımlanan klasik mekaniğin temel sorununa ufuk açıcı bir katkı yapmasıdır. Bu katkıyla -bütünleşebilir denklemlerin, gezegenler arasındaki kütle çekimsel etkileşimle ilişkili küçük etkiler yüzünden aynı denklemlerin artık “bütünleştirilemez” olduğu gerçeğiyle ilgili- derin bir niteliksel değişiklik ortaya çıkarır.
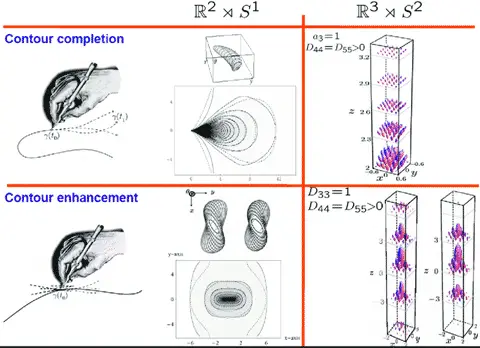
Kolmogorov’un bu büyük başarısı, Hamilton sistemlerinin mucidi olarak bilinen Hamilton’un (İrlandalı Matematikçi ve Astronom, 1805 – 1865) genel teorisinin geliştirilmesine katkı sağlar. Alanda yapılan sonraki hesaplamalar, Kolmogorov’un görüşlerine uygun bir şekilde doğrulanır ve son zamanlarda popüler olan dinamik sistemlerdeki “kaos” kavramının çalışma kapılarını aralar. Yapmış olduğu çalışmalarla günümüzde daha iyi hava tahminleri elde edilmektedir.
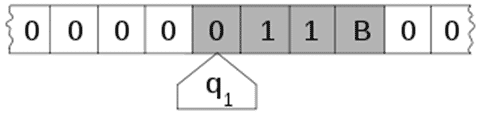
Aynı dönemde otomata teorisi (teorik bilgisayar biliminde, soyut makineleri kullanarak hesaplama problemlerinin çözülebilmesini araştıran dal) ve algoritma teorisi üzerinde çalışmaya başlar. Öğrencisi Vladimir Andreyeviç Uspensky (Rus Matematikçi, 1930 – 2018) ile birlikte, Kolmogorov-Uspensky (Kolmogorov-Uspensky Machine-KUM) makinesinin önemli kavramlarını formüle eder.
Sibernetik (canlı ve cansız tüm karmaşık sistemlerin denetlenmesi ve yönetilmesini inceleyen bilim dalı) alanı üzerine yapılan çalışmaları da desteklediğinden birçok Rus bilgisayar bilimcisi Kolmogorov’un öğrencileridir.
Kolmogorov’un 1955-1959 arasındaki ikinci dönemi, bilgi teorisi üzerinden dinamik sistemlerin ergodik teorisine uygulamalarından oluşur. Metrik uzaylar ve dinamik sistemler çalışmasında Kolmogorov, Vladimir Igorevich Arnold ile birlikte (Rus Matematikçi, 1937 – 2010) Hilbert’in (Alman Matematikçi, 1862 – 1943) 13. problemini çözer (herhangi bir sayıdaki değişkenin sürekli fonksiyonun, tek bir değişken ve toplamının sürekli fonksiyonlarının bileşimi olarak temsil edilebileceğini gösterir).
Dinamik sistemler teorisine entropik (termodinamik terimidir; rasgelelik ve düzensizlik kavramlarını temsil eder) özellikler getirme fikri, geniş ve yeni bir çalışma alanı ortaya çıkarır.
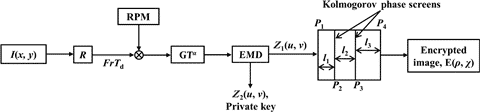
Bir diğer önemli kavram olan yarı düzenli bir sistem (şimdi K sistemi olarak adlandırılır) çözümlemesiyle fizik, biyoloji ve kimya alanlarında (güçlü stokastik özelliklere sahip klasik dinamik sistemlerin analizinde) çok önemli bir rol oynayan Kolmogorov, 1958-1959 yıllarında kendinden sonraki çalışmalar üzerinde büyük etkisi olan türbülans türü fenomenlere ergodik teorisinin uygulanması üzerine yaptığı çalışmaları yayınlar.
Sonraki Yıllar: 1960-1987
Kolmogorov başlarda matematik bilimlerinde bilgi teorisi kavramlarını kullanırken, sonraki yıllarda enformasyon teorisinin algoritma teorisi üzerine yeniden yapılandırılmasına çalışır. Tesadüfi olasılık teorisine mantıksal-algoritmik temeller vererek araştırma çemberi oluşturur. “Algoritmik Bilgi Teorisi”- “Kolmogorov karmaşıklığı” ile Kolmogorov, günümüz bilgisayarların gelişiminin öncüsüdür.
Olağanüstü bilimsel kariyerinin belki de son matematiksel yeniliğini Kolmogorov, 1973’te bağımsız sonlu kombinatoryal ilkeler üzerine istatistiksel bir teori bulmasıyla yapmıştır. Bu çalışmanın tekniğiyle elde edilecek yeni istatistikler, Kolmogorov karmaşıklığı cinsinden ifade edilir. Bireysel veriler ve onların modeli arasındaki ilişki, Kolmogorov’un Yapı İşlevi’nde anlatılmış ve bu çalışma; istatistiklere ve model seçimine olasılıkçı olmayan bir yaklaşım gerektirmesi bakımından önemli bir bakış açısı sunmaktadır.
Öğretmenliğe Bakış Açısı
Kolmogorov’un pedagojik faaliyetleri, Halk Eğitim Komiserliği Deneysel Model Okulunda öğretmen olduğu 1922 yılında başlar. Orada 1925’e kadar öğretmenlik yapar ve hemen ardından 1925’ten 1929’a kadar üniversitede öğretim görevlisi olarak çalışır.

Bilgi ve bilimsel fikirlerin aktarılması Kolmogorov için çok önemlidir. Bu konudaki ilgisi, ilk eğitimden yükseköğretime kadar geniş bir yelpazeye yayılmış ve zamanının çoğunu işgal etmiştir. Öğrencilerine göre Kolmogorov, çalışma alanları yaratan ve tam bağımsızlık veren bir eğitimcidir. Öğrencinin kişiliğine saygı duymuş ve onlara gereksiz müdahalelerden kaçınmıştır. Okullarda matematik olimpiyatlarının düzenlenmesinde aktif olarak yer almış ve okul çocuklarına konuşmalar yapmıştır. On binlerce nüsha halinde dağıtılan “Meslek Olarak Matematik” konulu bir kitapçık yazan Kolmogorov bu yazısında, matematikçi olmasalar dahi kariyerlerinde matematik eğitimine ihtiyaçları olacağı için, matematiksel olarak üstün yetenekli ergenlerin seçimine özel bir vurgu yapmıştır.
O’nun gözlemlerine göre, 14-15 yaşlarındaki öğrencilerin yaklaşık yarısı, matematik ve fizik derslerinin onlara pek faydası olmayacağı sonucuna ulaştıklarından; eğitmenlerin bu oranın farkında olmalarını ve basitleştirilmiş özel bir program ile bu tür öğrencilerini takip etmelerini önermiştir. Kolmogorov bilimsel çalışmalarla ilk kez tanışan gençleri, kendi başlarına özgün bir şey yapabileceklerine bir an önce ikna etmenin önemli olduğunu vurgulamıştır.

Öğrenciye araştırma konusunu sunarken danışmanın sadece konunun nesnel önemi hakkında değil; aynı zamanda konuyla ilgili çalışmanın genç bilim insanının gelişimini teşvik edip etmeyeceğini, gerçekleştirme yetkisini ve göstereceği azami çabayı takip etmesinin gerekli olduğunu belirtmiştir.
Bu anlayışla, 6. sınıftan 10. sınıfa kadar geometri, cebir ve analiz üzerine ders kitaplarının yazımında yer almış; “Kolmogorov Okulu” olarak bilinen Moskova Üniversitesi’ndeki yatılı matematik okulunda, yıllarca haftada 26 saat ders vermiş ve müfredatlar yazmıştır. Ayrıca öğrencilerin müzik, sanat ve edebiyat derslerine de katılmış ve entelektüel gelişimin akademik gelişime eşit olarak dengelenmesi gerektiğini söylemiştir. Bu okulun eski öğrencileri çok başarılıdır hatta Uluslararası Matematik Olimpiyatları’nda birinci olmuşlardır. Kolmogorov’un doktora derecesini almış araştırma öğrencilerinin sayısı altmışı aşar. Kendi ülkesinde matematik eğitiminin düzenlenmesinde önemli bir figür olmuştur.
Bilimsel Kariyeri
Kolmogorov, 1920’de başladığı üniversite eğitiminden 1925 yılında mezun olur ve 1929 yılında doktora derecesini alır. 1931 yılına gelindiğinde ise daha 28 yaşındayken Moskova Üniversitesi’nde Profesör olur.
1933 – 1939 yılları arasında aynı üniversitede “Bilimsel Araştırma Matematik Enstitüsü Müdürü” olarak görev yapar. Bu görevi esnasında tüm yüksek lisans öğrencilerinin bilimsel araştırmalarıyla da ilgilenir ve gerek mezun gerekse akademideki öğrencileriyle düzenlemiş olduğu Pazar günü yürüyüşleri bir klasik halini alır. 1939’da Kolmogorov, All-Union Bilimler ve Fizik-Matematik Bölümü Akademilerine seçilir. Yabancı Edebiyat Yayınevi’nin matematik yayın kurulu başkanı ve Büyük Sovyet Ansiklopedisi’nin matematik bölümünün editörü olarak muazzam işler yapar.

1964’ten 1966’ya ve 1976’dan 1983’e kadar Kolmogorov, Moskova Matematik Derneği’nin Başkanı; 1946’dan ölümüne değin Uspekhi Math’ın Genel Yayın Yönetmeni olur. Moskova Üniversitesinde 1938’den 1966’ya kadar olasılık teorisi dalının başkanlığını yapar. 1966’dan 1976’ya kadar Bölümlerarası İstatistiksel Yöntemler Laboratuvarı’nın başkanıdır ve 1976 – 1980 yılları arasında ise matematiksel istatistik dalının başkanlığı görevini yürütür. 1980’den itibaren ise bu görevinden matematiksel mantık dalında başkanlık yapmak için ayrılır.
1951’den 1953’e kadar Moskova Devlet Üniversitesi Matematik ve Mekanik Enstitüsü Müdürü; 1954’ten 1956’ya ve 1978’den 1983’e kadar Mekanik ve Matematik Fakültesi Matematik Bölümünün Başkanı olarak çalışır. 1954 – 1958 tarihleri arasında ise aynı üniversitenin aynı fakültesinde Dekan olarak görev yapar.
1964’te Kolmogorov, SSCB Bilimler Akademisi ile Pedagojik Bilimler Akademisi’nin ortak müfredat komitesinin matematiksel bölümünün başına geçmiştir. Bunun yanında Moskova Üniversitesi’nde bir İstatistik Laboratuvarı düzenlemiş ve Bolzano ödülünden kazandığı paranın bir kısmı ve büyük fonlar kullanarak oluşturduğu kütüphaneyi, uluslararası literatür çalışmalarını ekleyerek, genişletmiştir. 1972’de Kolmogorov’un girişimiyle matematiksel mantık zorunlu bir ders olarak ilk kez Moskova Devlet Üniversitesi Mekanik ve Matematik Bölümü’nde tanıtılmış ve müfredatını kendi yazmıştır. Eğitimi veren ilk kişi yine kendisidir.
Kolmogorov’un zengin bilimsel katkılarını şöyle özetleyebilirim: Trigonometrik seriler teorisi, ölçü teorisi, küme teorisi, entegrasyon (uyum) teorisi, yapıcı mantık (sezgisellik), topoloji, yaklaşım teorisi, olasılık teorisi, rastgele süreçler teorisi, bilgi teorisi, matematiksel istatistik, dinamik sistemler, otomata teorisi, algoritma teorisi, matematiksel dilbilim, türbülans teorisi, gök mekaniği diferansiyel denklemleri, Hilbert’in 13. problemi, balistik ve matematiğin biyoloji, jeoloji ve metallerin kristalizasyonu problemlerine uygulamalarıdır.

300’den fazla araştırma makalesi, ders kitabı ve sayılar teorisiyle birlikte matematiğin hemen hemen her alanını kapsayan araştırmaları ile kendisinin bir deha olarak kabul edilme sebebini anlamak artık daha kolay olmaktadır. Tüm bu alanlardaki kısa katkıları bile sadece bir soruyu incelemekle kalmamış; aksine temel kavrayışları ve derin ilişkileri ortaya çıkararak tamamen yeni araştırma alanları başlatmıştır.
Kolmogorov’a, o zamanlar SSCB olan Rusya tarafından Lenin Nişanı ve ayrıca Sosyalist Emek Kahramanı unvanı verilmiş; pek çok devlet tarafından ödüllendirilmiştir. Kendisini üye olarak seçen yabancı akademiler ve bilimsel toplulukların sayısında tüm Sovyet matematikçileri arasında ilk sırada yer almaktadır. Bazı önemli topluluklara üyeliği aşağıdaki gibidir:
- Hollanda Kraliyet Bilimler Akademisi (1963),
- Londra Kraliyet Derneği (1964),
- ABD Ulusal Topluluğu (1967),
- Paris Bilimler Akademisi (1968),
- Polonya Bilimler Akademisi,
- Romanya Bilimler Akademisi (1956),
- Alman Bilimler Akademisi (1959),
- Boston’daki Amerikan Bilim ve Sanat Akademisi (1959).
Paris, Berlin, Varşova, Stockholm, vb. üniversitelerinden fahri doktora unvanı verilmiştir. Londra Kraliyet İstatistik Derneği, Moskova Uluslararası İstatistik Enstitüsü, Londra, Hindistan ve Kalküta Matematik Dernekleri ile Amerikan Meteoroloji Derneği fahri üyesi seçilmiştir. 1963’te Uluslararası Bolzano ödülüne layık görülmüştür.

Hayatı boyunca bunların dışında da pek çok ödüle layık görülen Kolmogorov, daha çok olasılık teorisine sunduğu katkılarla tanınsa da Kolmogorov Karmaşıklığı ile Algoritmik Bilgi Teorisini geliştirmiş ve günümüz bilgisayarlarının gelişiminin öncüsü de olmuştur. Bilgi birikimi tarihten biyolojiye, fizikten kimyaya mühendislikten matematiğe pek çok bilimsel alanı kapsamaktadır.
Parkinson hastalığından muzdarip ve hayatının son birkaç yılını neredeyse görme engelli olarak geçirmesine rağmen ölünceye kadar matematik dünyasına aktif bir ilgi göstermeye devam etmiştir. Siyasi yaşamdan uzak bilimsel anlayışı ve eğitmen kimliği ile kuşkusuz ki çağının ötesinde bir isim olan Kolmogorov, idealist kişiliği ile de saygıyı hak etmekte ve pek çok insana ilham kaynağı olmaya devam etmektedir.
Kaynakça:
- Andrey Nikolayevich Kolmogorov. (Erişim Tarihi: 21.07.2020);https://www.britannica.com/
- Andrey Nikolayevich Kolmogorov. (Erişim Tarihi: 21.07.2020);https://mathshistory.st-andrews.ac.uk
- A Short Biography of A.N. Kolmogorov. (Erişim Tarihi: 12.07.2020);https://homepages.cwi.nl/
- Remembering Kolmogorov. (Erişim Tarihi: 03.09.2020);https://www.researchgate.net/
Matematiksel










