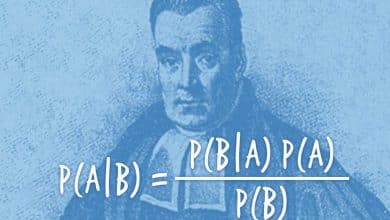Finans piyasaları karmaşıktır ve fiyatlar sürekli olarak değişir. Yatırımcılar, bu dalgalanmalar karşısında risklerini yönetmek ve kazançlarını en üst düzeye çıkarmak için matematiksel modeller geliştirirler. Black-Scholes denklemi, bu modellerin en ünlülerinden biridir ve opsiyon fiyatlamasında devrim yaratan bir yaklaşım sunar.

Kapitalist ekonominin temel kurallarından biri, kâr elde etmek için risk almanın zorunlu olduğudur. İlke olarak, alınan risk büyüdükçe potansiyel kazanç da artar. Bunun karşılığında işler planlandığı gibi gitmezse büyük kayıplara da hazırlıklı olmak gerekir.
Uzun süre boyunca, yasal sınırları aşmadan bu riski ortadan kaldırmanın ya da güvence altına almanın neredeyse imkânsız olduğu düşünülmüştür. Ancak birkaç on yıl önce ekonomistler, bu durumu kökten değiştirecek nitelikte bir matematiksel formül geliştirdiklerini öne sürdüler.
Riski daha etkin biçimde kontrol etmeyi amaçlayan bu “sihirli formül”, ilk kez 1973 yılında Fischer Black ve Myron Scholes tarafından yayımlandı. Black–Scholes denklemi geliştiricileri büyük ün kazandı, servet edindi ve 1997 yılında Nobel Ekonomi Ödülü’ne layık görüldü.

O döneme kadar finans dünyasında pek kullanılmayan bu tür matematiksel araçlar, yatırım bankalarının dikkatini çekti. Bunun sonucunda bankalar, karmaşık matematiksel problemleri çözebilen fizikçi, matematikçi ve mühendisleri işe almaya başladı.
Black–Scholes modeli, bir dönem opsiyon borsalarında çalışan işlemciler için adeta Kutsal Kâse niteliğindeydi. İşlemciler, birbirlerine ve Black–Scholes modelinin öngördüğü teorik değere göre yanlış fiyatlanmış iki opsiyonu tespit ederdi. Teorik değerine kıyasla düşük fiyatlanan opsiyonu satın alır, yüksek fiyatlananı ise satarlardı.
Ardından zamanın geçmesiyle fiyatların yeniden dengeye gelmesini bekler ve bu farktan kâr elde etmeyi amaçlarlardı. Bu strateji tekil bir işlemde her zaman başarı sağlamasa bile, model uzun vadede doğruysa, ortalamalar yasası —yani her bir işlemin pozitif beklenen değere sahip olması— yatırımcıya zamanla kâr sağlayacaktı.
Opsiyon Nedir ve Neden Önemlidir?
Opsiyonlar, sahibine belirli bir süre içinde, önceden belirlenmiş bir fiyattan bir şeyi satın alma hakkı veren sözleşmelerdir; ancak bu hakkı kullanma zorunluluğu yoktur. Yani opsiyon, belirsizlik karşısında alınan bir tür sigorta gibidir.
Bunu günlük bir örnekle düşünelim. Bir film şirketi, ileride bir film çekmeyi planlıyor ama henüz kesin karar vermiş değil. Yine de başrol için çok uygun bir oyuncunun başkasıyla anlaşmasını istemiyor. Bu yüzden oyuncuya küçük bir bedel ödeyerek şu hakkı satın alıyor: “Eğer filmi çekmeye karar verirsem, seni önceden belirlediğimiz ücretle oynatabilirim.”
Film çekilirse şirket avantajlı bir anlaşma yapmış olur; çekilmezse yalnızca bu küçük bedeli kaybeder. Oyuncu açısından bakıldığında ise, film çekilmese bile aldığı ücret kendisinde kalır. Taraflardan hiçbiri zorunlu bir yükümlülük altına girmez.
Hisse senedi opsiyonları da aynı mantıkla çalışır. Bir yatırımcı, bir hisseyi gelecekte belirli bir fiyattan satın alma hakkını bugün satın alır. Hissenin fiyatı yükselirse bu hakkı kullanır, düşerse kullanmaz. Başlangıçta bu tür sözleşmeler karmaşık ve bire bir pazarlıkla yapılırken, 1950’li ve 1960’lı yıllarda yatırımcıların ilgisi arttı.
Bunun sonucunda 1970’lerin başında opsiyonların standartlaştığı ve borsalarda işlem görmeye başladığı bir piyasa ortaya çıktı. Aynı dönemde, iki parlak matematiksel iktisatçı olan Fischer Black ve Myron Scholes, bir hisse senedi opsiyonunun değerini hesaplayan matematiksel bir ifade türetti.
Black Scholes Denklemi Nedir?
Black–Scholes denklemi, fizikteki ısı denklemiyle benzerlik gösteren bir kısmi diferansiyel denklemdir. Bu benzerlik şaşırtıcı değildir. Bir gazın molekülleri rastgele hareket eder, sayısız küçük çarpışma ve sapma yaşar. Piyasa fiyatları da benzer biçimde dalgalanır. Bu yüzden, nasıl ki moleküllerin ortalama davranışı sıcaklıkla tanımlanıyorsa, piyasa fiyatlarının ortalama hareketi de benzer matematiksel denklemlerle açıklanır.
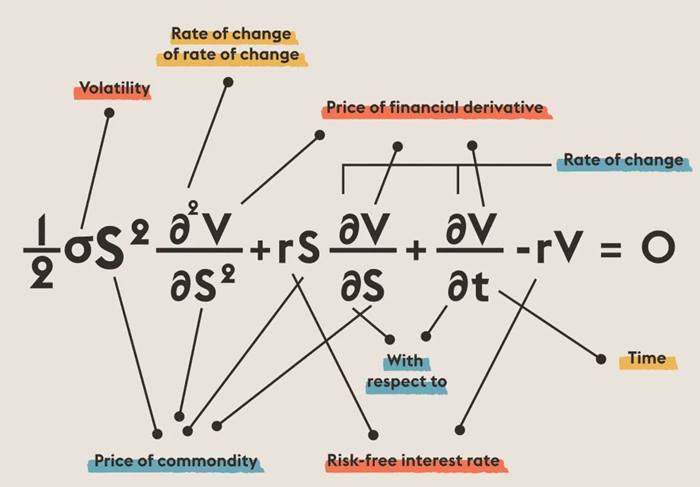
Dayanak varlığın fiyatı (S): Opsiyonun bağlı olduğu varlığın (örneğin bir hisse senedi) güncel piyasa fiyatı.
Risksiz faiz oranı (r): Genellikle devlet tahvilleri gibi güvenli yatırım araçlarının getirisi olarak kabul edilmektedir.
Oynaklığı (σ), yani fiyat değişimlerinin ne kadar dalgalandığını gösteren ölçüttür.
Black–Scholes denklemi, bazı basitleştirici finansal kabullerden yola çıkılarak türetilmiştir. Model, işlem maliyetlerinin bulunmadığını, açığa satışın serbest olduğunu ve paranın bilinen, sabit ve risksiz bir faiz oranıyla borç alınıp verilebildiğini varsayar.
Model ayrıca piyasa fiyatlarının istatistiksel olarak Brown hareketine benzediğini kabul eder. Buna göre fiyatların ortalama yönelimi ve piyasadaki dalgalanma düzeyi zaman içinde değişmez. Dalgalanma, fiyatların ortalama değerden ne kadar saptığını gösteren bir ölçüdür.
Asıl sorun, beklenmedik olayların devreye girdiği anlarda ortaya çıkar. Bu tür olaylar piyasa davranışını ani ve büyük ölçekte etkiler. Böyle durumlarda Black–Scholes denkleminin varsayımları geçerliliğini yitirir ve model gerçekliği açıklamakta yetersiz kalır.
Black–Scholes denklemi, vadeli işlemler piyasasına rasyonel bir fiyatlama yöntemi kazandırmak için geliştirilmiştir. Bir opsiyonun vadesi dolmadan önceki değerini sistematik biçimde hesaplamayı sağlar. Ayrıca bu opsiyonun piyasada adil bir fiyattan alınıp satılmasına imkân verir.
Basit bir örnek düşünelim. Bir tüccar, 12 ay sonra ton başına 500 birim fiyattan 1000 ton pirinç satın almak üzere bir sözleşme yapmış olsun. Bu sözleşme bir alım opsiyonudur. Beş ay geçtikten sonra tüccar, bu opsiyonu satın almak isteyen birine satmaya karar verir. Peki, bu sözleşmenin bugünkü değeri nedir? Black–Scholes denklemi bu soruya cevap verir.
Black Scholes Denklemi İle İlgili Sorun Nedir?
Finans sektörü, Black–Scholes denkleminin avantajlarını hızla benimsedi ve farklı varsayımlara dayanan, farklı finansal araçlara uyarlanmış çok sayıda benzer model geliştirdi. Geleneksel bankacılık dünyası bu denklemleri, riskleri gözeterek kredi ve işlem kararlarını gerekçelendirmek için kullandı. Ancak daha az temkinli alanlarda faaliyet gösterenler, modele neredeyse sorgusuz bir inançla sarıldı.
Bu çalışmalar, ekonomi alanında bir Nobel Ödülü’ne giden yolu açtı. Aynı zamanda Long-Term Capital Management (LTCM) adlı hedge fonunun kurulmasına da zemin hazırladı. Fonun yönetim kurulunda Scholes’un yanı sıra, Robert Merton ve John Meriwether yer alıyordu.
LTCM ilk iki yılında yüzde 40, üçüncü yılında ise yüzde 27 getiri sağladı. 1994 ile 1998 yılları arasında LTCM fonu yatırımcılarına iyi getiriler sağladı. Aynı dönemde fon, Rusya gibi gelişmekte olan piyasalarda da büyük pozisyonlar aldı.
Ancak 1998’de dört aydan kısa sürede 4,6 milyar dolar kaybetti. Bunun üzerine ABD Merkez Bankası, büyük alacaklıları 3,6 milyar dolarlık bir kurtarmaya ikna etti. Bankalar paralarını geri alsa da LTCM 2000 yılında tasfiye edildi.
Görüşler farklı olsa da genel kabul, LTCM’nin çöküşünü tetikleyen yakın nedenin 1998 Rusya finansal krizi olduğudur. Batılı piyasalar Rusya’ya yoğun yatırım yapmıştı; Rus ekonomisi ise büyük ölçüde petrol ihracatına bağlıydı. 1997 Asya krizi petrol fiyatlarını düşürdü ve bu durum Rus ekonomisini sert biçimde vurdu.
Asıl sorun ise baştan beri mevcuttu. Modeller, belirli varsayımlara dayanıyordu ve bu varsayımlar geçerliliğini yitirdiği anda LTCM ciddi risk altına girdi. Rusya krizi, özellikle oynaklığın sınırlı olduğu ve aşırı dalgalanmaların nadiren yaşandığı kabulünü geçersiz kıldı.
Okuma önerisi: Para İle İlgili İlginç Bir Soru: Zengin Konuk Paradoksu
Sonuç Olarak
Black–Scholes denklemi, bir yandan trilyonlarca dolarlık dev bir finans endüstrisinin doğmasına yol açarak dünyayı değiştirdi. Öte yandan, denklemin genelleştirilmiş hâllerinin sorgusuzca kullanılması, finansal çöküşlere katkıda bulundu.
Bir denklem bir araçtır; her araç gibi onu kullanan kişinin ne yaptığını bilmesini ve doğru amaçla kullanmasını gerektirir. Araçların başarısızlığının sorumluluğu, onları nasıl kullandığını bilen ya da bilmeyen insanlara aittir.
Kaynaklar ve ileri okumalar:
- The mathematical equation that caused the banks to crash. Yayınlanma tarihi: 12 Şubat 2012. Kaynak site: Guardian. Bağlantı: The mathematical equation that caused the banks to crash
- A risky business: how to price derivatives. yayınlanma tarihi: 1 Kasım 2018; Bağlantı: https://plus.maths.org/
Matematiksel