Matematik çoğu insanı duygusal olarak etkilemez. Buna rağmen Barok dönem Alman bestecisi Johann Sebastian Bach’ın müziği bizi derinden etkiler. Bugün bilgi kuramından yararlanan araştırmacılar, Bach’ın bu duygusal etkileyiciliği nasıl yarattığını adım adım çözmeye başlıyor.

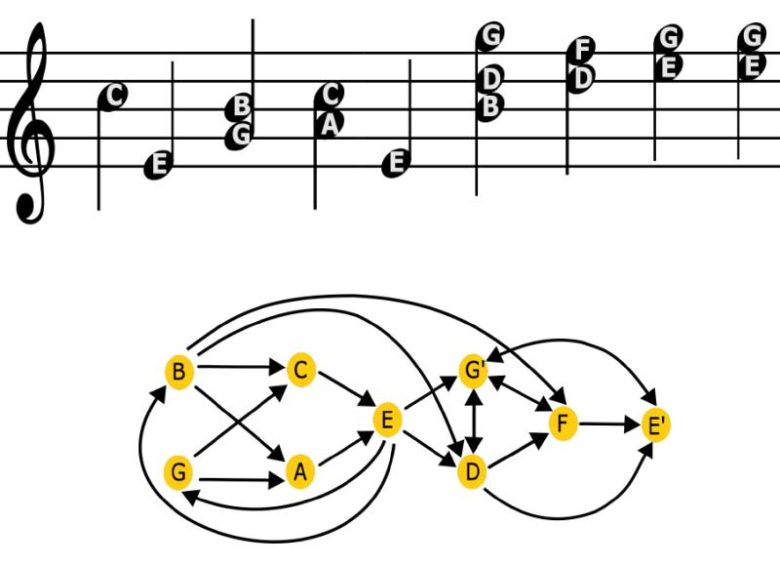
Araştırmacılar, Bach’ın yüzlerce bestesini incelemek için notaları, “düğüm” adı verilen noktalar ve bu düğümleri birbirine bağlayan “kenar” adı verilen çizgilerle basit ağlara dönüştürdü. Bu sayede eserlerin ilettiği bilgiyi nicel olarak ölçebildiler.
Analiz, Bach’ın farklı müzik türlerinin ne kadar bilgi taşıdığı açısından belirgin biçimde ayrıldığını ortaya koydu. Ayrıca bu müzikal ağların, dinleyicinin mesajı daha kolay anlamasını sağlayabilecek yapılar içerdiği de görüldü.

Araştırmacılar, basit ezgi dizilerinden karmaşık müzikal ağlara kadar tüm yapıları ölçmek için 1948’de matematikçi Claude Shannon tarafından ortaya atılan bilgi entropisi kavramını kullandı. Bu yöntemle, bir müzik parçasının ne kadar bilgi içerdiği sayısal olarak ifade edilebildi.
Bilgiyi Ölçmek Mümkün mü?
21. yüzyıl teknolojilerine en çok katkı sağlayan isimlerden biri şüphesiz Claude Shannon’dur. En çok bilgi teorisinin kurucusu olarak tanınan Shannon, 1948’de yayımladığı “A Mathematical Theory of Communication” adlı çalışmasında iletişimi matematiksel bir modelle tanımlayarak bu alanın temellerini atmıştır.
Bu kuramsal çerçeve, dijital çağın veri iletimi, kodlama, sıkıştırma ve güvenlik sistemleri gibi pek çok temel teknolojisinin gelişmesini mümkün kılmıştır.
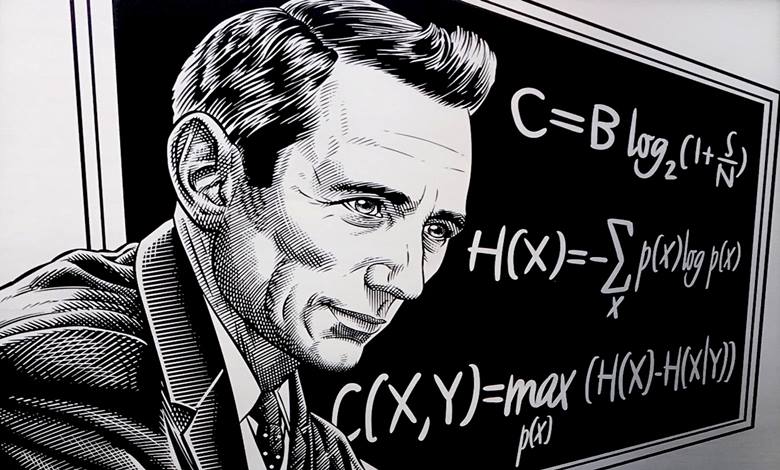
Bilgi entropisi hem matematiksel hem kavramsal olarak termodinamik entropiyle ilişkilidir. Temel olarak, bir mesajın ne kadar “şaşırtıcı” olduğunu ölçer. Buradaki “mesaj” kavramı yalnızca metin ya da sayı dizisi değil, bir müzik parçası gibi bilgi içeren her şeyi kapsar.
Bu yaklaşım ilk bakışta sezgilere aykırı gelecektir. Sonucunda günlük dilde bilgi genellikle kesinlik ile özdeşleşmiştir. Ancak bilgi entropisinin temel fikri şudur: Zaten bildiğiniz bir şeyi öğrenmek, aslında hiçbir şey öğrenmemektir.
Sadece tek bir şey söyleyebilen biriyle yapılan bir konuşm tamamen öngörülebilir olur, ancak neredeyse hiçbir bilgi taşımaz. Benzer şekilde, yalnızca tek bir notadan oluşan bir müzik parçası, beynin kolayca öğrenebileceği veya zihinsel olarak yeniden üretebileceği kadar basit olur. Ancak anlam ya da mesaj iletmek konusunda yetersiz kalırdı.
Bu yaklaşıma göre müziği “öğrenmek”, duyduğumuz gerçek seslerin zihnimizde doğru temsillerini, yani araştırmacıların “model” dediği yapıları oluşturmak anlamına gelir. Bu süreç, beklenti ile sürprizin etkileşimiyle ilerler. Zihinsel modelimiz, daha önce duyduklarımıza bakarak bir sonraki sesin gelme olasılığını tahmin eder.
Bach’ın Müziği Ne Tür Bir Bilgi Aktarıyor ve Bu Ne Anlama Geliyor?
Fizikçi Kulkarni ve çalışma arkadaşları, insanların müzikten anlam çıkarırken izledikleri yolları anlamak amacıyla, bilgi kuramı araçlarını kullanarak olası bilgi yapıları aradı. Bu kapsamda, Bach’ın 337 bestesini birbirine bağlı düğümlerden oluşan ağlara dönüştürdüler. Ardından bu ağların bilgi entropisini hesapladılar.
Ancak toccatalar ve prelüdler, insanları eğlendirmeyi ve şaşırtmayı amaçlıyordu. Karmaşıklıkları sayesinde de bol miktarda bilgi iletiyorlardı. Daha sonra araştırmacılar, her bir müzik ağının toplam bilgisini, bir insan dinleyicinin bundan toplayabileceği bilgi miktarıyla karşılaştırdı.
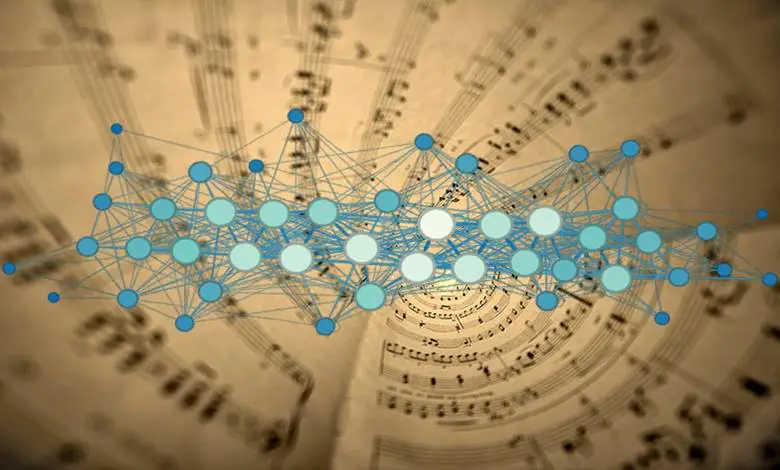
Araştırmacılar, Bach’ın müziğinde notalar arası geçişlerden oluşan ağların, aynı büyüklükte rastgele ürettikleri ağlardan daha fazla bilgi içerdiğini ortaya koydu. Bu fark, her düğüme bağlı kenar sayısındaki çeşitliliğin artmasından kaynaklandı.
Ayrıca araştırmacılar, Bach’ın farklı bestecilik tarzlarının bilgi yapısı ve içeriğinin değiştiğini belirledi. İlahi türündeki korallerdeki ağlar, bilgi açısından görece seyrek olmasına rağmen aynı büyüklükteki rastgele ağlardan yine de daha zengin çıktı. Buna karşılık, genellikle org, klavsen veya piyano gibi klavyeli çalgılar için yazılan toccata ve prelüdler, daha yüksek bilgi entropisi sundu.
Sonuç Olarak
Bu çalışma, ilk bakışta size çok önemli bir bulgu gibi görünmeyebilir. Ancak araştırmacılar, bir sanat eserini matematiksel yöntemlerle inceleyerek başlı başına değerli bir adım attı. Yeni çalışmalar, sanatçılar, sosyologlar, müzikologlar ve sinirbilimciler arasında ortak bir çalışma zemini oluşturacak. Son olarak Shannon, “doğası ne olursa olsun bilgi ölçülebilir” derken haklıydı.
Kaynaklar ve ileri okumalar
- Secret Mathematical Patterns Revealed in Bach’s Music. Yayınlanma tarihi: 16 Şubat 2024. Kaynak site: Scientific America. Bağlantı: Secret Mathematical Patterns Revealed in Bach’s Music
- Kulkarni, Suman & David, Sophia & Lynn, Christopher & Bassett, Dani. (2023). Information content of note transitions in the music of J. S. Bach. ArXiv.
- Measuring the Information Delivered by Music. Yayınlanma tarihi: 2 Şubat 2024. Kaynak site: Physics. Bağlantı: Measuring the Information Delivered by Music
Size Bir Mesajımız Var!
Matematiksel, mde matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel