1913 yılında Rus matematikçi Andrey Andreyeviç Markov, St. Petersburg’daki çalışma odasında Aleksandr Puşkin’in bir romanıyla oturuyordu. Ancak Markov’un amacı bu kitabı okumak değildi.

Bunun yerine bir kalem ve kâğıt aldı; ardından, kitabın ilk 20.000 harfini aralardaki boşlukları ve noktalama işaretlerini çıkararak yan yana yazdı. Daha sonra bu harfleri, her biri 10×10 karakter içeren 200 ayrı ızgaraya yerleştirdi. Son olarak, her satır ve sütundaki sesli harfleri sayıp sonuçları topladı.
Dışarıdan bakan biri için Markov’un tüm bu yaptıkları tuhaf görünebilir. Ancak Markov, kitabı yaşam ya da insan doğası hakkında dersler çıkarmak için okumuyordu. O, metnin matematiksel yapısını araştırıyor ve 1909’dan beri geliştirdiği bir olasılık teorisini test ediyordu.

19. yüzyılda Rus matematikçiler bilim dünyasında iz bırakmaya başlamıştı. Nikolai Lobachevsky (1792–1856), Öklid dışı geometrinin öncülerindendi. Birkaç on yıl sonra Pafnuty Chebyshev (1821–1894), sayı teorisi ve olasılık kuramına önemli katkılar sağladı.
Chebyshev’in öğrencileri, bir sonraki nesil Rus matematikçilerinin çekirdeğini oluşturdu. Andrey Markov da bu grubun bir parçasıydı. Tüm kariyerini Chebyshev ve diğer meslektaşlarıyla birlikte St. Petersburg Üniversitesi’nde geçirdi. Bağlantılı olasılıklar zincirlerine ilişkin fikirlerini ise, emekli olduktan sonra geliştirmeye başladı.
Andrey Markov Neden Harfleri Saydı?
Olasılık teorisinin kökleri şans oyunlarına dayanır. Örneğin, adil bir madeni para attığınızda, yazı gelme olasılığı her zaman 1/2’dir. İkinci bir para attığınızda ise bu sonucun ilk atışla hiçbir bağlantısı yoktur. Bu bağımsızlık ilkesi, bileşik olasılıkların hesaplanmasını kolaylaştırır. Adil bir parayı iki kez havaya atarsanız, her iki seferde de yazı gelme olasılığı basitçe 1/2 × 1/2 = 1/4 olur.
Ancak bu mantık her zaman geçerli değildir. Yağmurlu bir günün olasılığının 1/3 olduğunu varsayalım. Bu, iki gün üst üste yağmur yağma olasılığının 1/3 × 1/3 = 1/9 olduğu anlamına gelmez.
Çünkü bazı durumlarda, gelecekteki olayların olasılıkları sistemin mevcut durumuna bağlıdır. Olaylar birbirine bağımlı hâle geldiğinde, Markov zinciri olarak bilinen yapılar ortaya çıkar.
Noktalardan ve oklardan oluşan bir diyagram, bir Markov zincirinin yapısını gösterir. Noktalar, sistemdeki durumları temsil eder; oklar ise bu durumlar arasındaki geçişleri belirtir. Her ok, o geçişin olasılığını temsil eden bir sayıyla ilişkilidir.
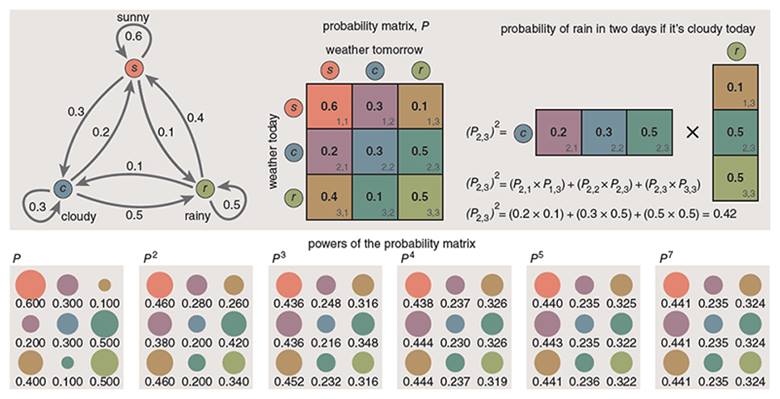
Bu sayılar olasılık değerleri olduğu için 0 ile 1 arasında yer alır. Ayrıca, bir noktadan çıkan tüm olasılıkların toplamı tam olarak 1’e eşit olmalıdır. Belirli bir durum dizisinin olasılığını hesaplamak için, sırayla gerçekleşen geçişlerin her birine karşılık gelen okların olasılıklarını birbiriyle çarpmanız yeterlidir.
Geçiş olasılıklarını içeren matrisin kendisine P diyelim. Eğer bu matris yarının hava durumunu tahmin ediyorsa, P × P ya da P² çarpımı, yarından sonraki günün olasılıklarını verir. P³ ise üç gün sonrasının durum olasılıklarını tanımlar.
Andrey Markov’un Çalışmasına Claude Shannon Katkısı
Andrey Markov, konuya yalnızca iki durumu olan bir sistemle çalışarak başladı. İzleyen birkaç yıl içinde bulgularını genelleştirdi. Bunu kanıtlamak için bir kitaptaki harfleri saymak ona göre doğru bir yaklaşımdı. Çünkü Markov, bir metindeki belirli bir harfin, belirli bir konumda yer alma olasılığının bir dereceye kadar ondan önce gelen harfe bağlı olduğunu göstermek istiyordu.

Ancak Markov hayattayken bu çalışması fazla ilgi görmedi ve 2006 yılına kadar araştırma makalesi İngilizceye çevrilmedi.
Bu durum, Claude Shannon’ın 1948’de yayımladığı İletişimin Matematiksel Teorisi (The Mathematical Theory of Communication) adlı makaleyle değişti. Shannon, bu makalesinde bir mesajdaki bilgi miktarını kesin olarak ölçmenin bir yolunu ortaya koydu ve bunu yaparken dijital çağı tanımlayacak bilgi teorisinin temelini attı.

Claude Shannon Bir Dil Üretilebileceğini Gösterdi
Shannon, Markov’un bir metinde bir harfin veya kelimenin görünme olasılığının yaklaşık olarak hesaplanabileceği fikrinden büyük ölçüde etkilenmişti.
Bunun ardından, tıpkı Markov gibi, Shannon da metinler üzerinde deneyler yapmaya başladı. Ancak o, istatistiksel kurallara göre metin üretmeye çalışarak bir adım daha ileri gitti. İlk kontrol deneyinde, 27 sembolden oluşan bir alfabe (26 harf ve bir boşluk) kullanarak rastgele harfler seçti ve bu yolla bir cümle oluşturmaya çalıştı. Elde ettiği çıktı şu şekildeydi:
XFOML RXKHRJFFJUJ ZLPWCFWKCYJ FFJEYVKCQSGHYD QPAAMKBZAACIBZLHJQD
İletişim kurarken harfleri eşit olasılıkla seçmediğimiz için ortaya çıkan cümle anlamsızdı. Ancak Andrey Markov’un da gösterdiği gibi, ünsüz harfler ünlülerden daha olasıdır. Ayrıca, E harfi S’den, S de Q’dan daha sık kullanılır. Shannon, bunu hesaba katarak orijinal alfabesini, İngilizcedeki harflerin kullanım olasılıklarını daha iyi yansıtacak şekilde yeniden düzenledi. Sonuç olarak, İngilizceye biraz daha benzeyen bir cümle elde etti.
OCRO HLI RGWR NMIELWIS EU LL NBNESEBYA TH EEI ALHENHTTPA OOBTTVA NAH BRL.
Shannon, gerçekleştirdiği bir dizi sonraki deneyde, istatistiksel model karmaşıklaştıkça ortaya çıkan sonuçların giderek daha anlaşılır hâle geldiğini gösterdi. Markov’dan ilham alarak, İngilizce dili için istatistiksel bir çerçeve ortaya koydu. Bu çerçeveyi kullanarak yalnızca dili analiz etmekle kalmayıp, aynı zamanda dil üretebileceğini de kanıtladı. Son deneyinde ise harfler yerine bir kelime kümesi kullandı ve şu sonucu elde etti:
THE HEAD AND IN FRONTAL ATTACK ON AN ENGLISH WRITER THAT THE CHARACTER OF THIS POINT IS THEREFORE ANOTHER METHOD FOR THE LETTERS THAT THE TIME OF WHO EVER TOLD THE PROBLEM FOR AN UNEXPECTED.
Sonuç olarak
Hem Shannon hem de Markov’un fikirleri, farklı türdeki problemleri yeniden düşünmek için güçlü bir yaklaşım sundu. Andrey Markov, olasılık teorisini bağımsız olayların ötesine taşıyarak yeni bir çağın kapısını araladı. Bu sayede, bugün Markov zincirleri ekonomi, biyoloji, bilgisayar bilimi, pazarlama ve daha birçok alanda uygulanmaktadır.
Örneğin, Google’ın kurucuları Larry Page ve Sergey Brin tarafından geliştirilen PageRank algoritması, durumların World Wide Web’deki sayfaları temsil ettiği bir Markov zincirine dayanır. Geçişler ise sayfalar arasındaki bağlantılardır.
Shannon’un çalışması da bir mesajdaki bilgi birimlerini ölçmenin ve kodlamanın kesin bir yolunu formüle etmesine yardımcı oldu. Bu da telekomünikasyonda ve sonunda dijital iletişimde devrim yarattı. Tüm bu çalışmalar, dijital çağdan günümüze kadar uzanan doğal dil işleme için de yeni bir çağın habercisi oldu.
Kaynaklar ve ileri okumalar
- Andrey Markov & Claude Shannon Counted Letters to Build the First Language-Generation Models. Yayınlanma tarihi: kaynak site: Bağlantı: Andrey Markov & Claude Shannon. Counted Letters to Build the First Language-Generation Models
- Markov , A.. (2006). An Example of Statistical Investigation of the Text Eugene. Onegin Concerning the Connection of Samples in Chains. Science in Context. 19. 591 – 600. 10.1017/S0269889706001074.
Matematiksel





