Veriye dayalı kararların giderek önem kazandığı günümüzde, matematiksel bir araç olan wavelet’ler (dalgacıklar), bilgiyi analiz etmek ve anlamlandırmak için vazgeçilmez hâle geldi.

Birçok araştırmacı, verilerini kesintisiz sinyaller hâlinde alır. Yani zamanla değişen, durmaksızın akan bilgi akışlarıyla çalışırlar. Örneğin bir jeofizikçi, yer altındaki kaya katmanlarından yansıyan ses dalgalarını inceler. Bir veri bilimci ise, bir görüntü tarayıcısından gelen elektrik sinyallerini analiz eder.
Bu tür veriler, karmaşık şekiller alır. Bu da onları anlamayı ve parçalara ayırarak incelemeyi zorlaştırır. Wavelet (dalgacık) adı verilen matematiksel araçlar, işte bu karmaşıklığı çözmek için kullanılır.
Wavelet Nedir?
Wavelet’ler, aslında çok eski ve güçlü bir matematiksel yöntemin, Fourier dönüşümünün, daha gelişmiş bir versiyonu olarak ortaya çıktı.
1807 yılında Joseph Fourier, periyodik fonksiyonların (yani belirli aralıklarla kendini tekrar eden değerler üreten denklemlerin), sinüs ve kosinüs gibi trigonometrik fonksiyonların toplamı olarak ifade edilebileceğini keşfetti. Bu yöntem, karmaşık sinyalleri daha basit bileşenlerine ayırmaya olanak tanıdığı için oldukça etkiliydi

Fourier dönüşümü, bu özelliği sayesinde bilimsel araştırmalarda ve teknolojide pek çok alanda kullanılmaya başlandı. Ancak wavelet’ler bu yönteme göre çok daha hassas analizler yapılmasına olanak tanır.
Fourier dönüşümünün en büyük eksiklerinden biri, sinyalde hangi frekansların bulunduğunu göstermesine rağmen, bu frekansların ne zaman ortaya çıktığı ya da ne kadar bulundukları hakkında bilgi vermemesidir. Bu durum, bir para yığını içindeki banknot türlerini bilip, her türden kaç tane olduğunu bilmemeye benzer.
Bu sorunu çözmeye yönelik ilk adımı, 1946’da Macar fizikçi Dennis Gabor attı. Sinyali kısa zaman dilimlerine bölüp öyle analiz etmeyi önerdi. Ancak bu yöntem, karmaşık sinyallerde yeterli olmadı.. Sonrasında Jean Morlet, frekansa göre pencere boyutunu ayarlayan bir yöntem geliştirdi. Düşük frekanslar için geniş, yüksek frekanslar için dar zaman pencereleri kullandı.
Morlet’in kullandığı zaman pencereleri, hâlâ gerçek hayattaki karmaşık frekansları içeriyordu ve bu frekansları analiz etmek oldukça zordu. Bu sorunu çözmek için Morlet, her sinyal parçasını bir dalgayla eşleştirme fikrini geliştirdi. Bu dalga desenlerine Fransızca “küçük dalgalar” anlamına gelen “ondelette” adını verdi. Terim, İngilizce’ye wavelet (dalgacık) olarak geçti.
Fourier Dönüşümünün Sınırları Vardır
Bu yaklaşımla bir sinyali, belirli dalga boylarına odaklanan küçük parçalara ayırmak ve her parçayı uygun bir dalgacıkla eşleştirerek analiz etmek mümkün hâle geldi. Elimizdeki banknot yığınına baktığımızda, artık her türden kaç adet bulunduğunu net biçimde görebiliyoruz.
Kabaca anlatmak gerekirse, belirli frekans ve şekildeki bir dalgacığı ham sinyalin üzerinde kaydırıyoruz. Dalgacık sinyalle uyumlu olduğunda, aralarındaki nokta çarpımı adı verilen matematiksel işlem sıfıra ya da çok yakın bir değere yaklaşıyor. Farklı frekanslardaki dalgacıkları sırayla kullanarak tüm sinyali tarayabiliyor ve sinyalin genel yapısını ayrıntılı biçimde ortaya koyabiliyoruz.
Dalgacıklar üzerine yapılan araştırmalar hızla ilerledi. Fransız matematikçi Yves Meyer, Morlet ve Grossmann’ın çalışmalarından etkilenerek bu alana yöneldi. Daha sonra aralarına Ingrid Daubechies de dahil oldu. Bu ekip, dalgacık kuramının temellerini atarak alanın gelişmesinde önemli rol oynadı. Meyer, dalgacık kuramı üzerine yaptığı bu çalışmalarla Abel Ödülü’nü kazandı.

Bir süre sonra, Pennsylvania State University’den Stéphane Mallat, Meyer’in dalgacık kuramıyla tanıştı ve onunla birlikte çalışmaya başladı. 1986’da, dalgacıkların görüntü analizinde kullanımını ele alan bir makale yayımladılar. Bu çalışma, daha sonra dünya genelinde kullanılan JPEG2000 görüntü sıkıştırma yönteminin temelini oluşturdu.
JPEG2000, görüntüleri daha az yer kaplayacak şekilde sıkıştıran bir teknolojidir. Dalgacık (wavelet) analizini kullanarak görüntüdeki veriyi daha verimli temsil eder. Böylece dosya boyutu küçülürken görüntü kalitesi korunur. Özellikle yüksek çözünürlüklü verilerin iletiminde ve saklanmasında avantaj sağlar.
Wavelet’ler Nerelerde Karşımıza Çıkar?

(A) Örneğin Van Gogh’un Patch of Grass (1) adlı tablosunun altında, farklı bir tablo yer alıyor. Bu tür gizli katmanlara “alt boyama” (2) denir. X-ray taramalarıyla bu gizli görüntüler ortaya çıkar. Ardından, dalgacıklar kullanılarak orijinal görüntü yeniden oluşturulur. (3–4). Bu yöntem, hem sanat tarihçilerine hem de restorasyon uzmanlarına önemli bilgiler sunar.
Dalgacıkları bu kadar kullanışlı kılan özelliklerinden biri, neredeyse her tür veriye uyum sağlamalarıdır. Farklı biçimlerde, boyutlarda ve frekanslarda ayarlanabilirler; bu da onları çok yönlü hale getirir.
Matematikçiler, farklı sinyal türlerine uyum sağlamak için çeşitli dalgacık “aileleri” geliştirmiştir. Bu esneklik sayesinde, görüntülerdeki veya sinyallerdeki karmaşık desenler bile etkili şekilde analiz edilmektedir.
Dalgacıkların en bilinen türlerinden biri, fraktal yapısıyla öne çıkan Daubechies ailesidir. Bu dalgacıklar, görüntü analizinde o kadar hassastır ki, uzmanlar onları sahte Van Gogh tablolarını ayırt etmekte bile kullanmıştır.
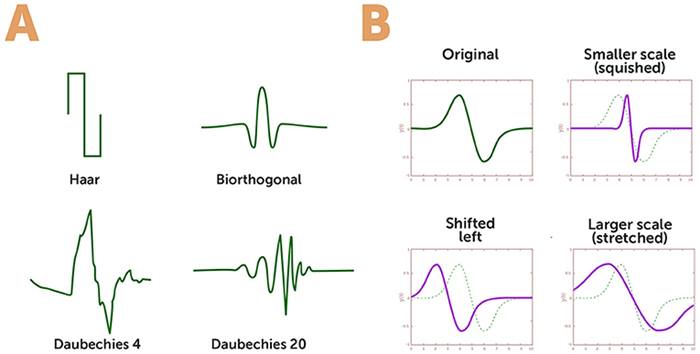
Diğer tanınmış dalgacıklar arasında, ortasında büyük bir tepe ve yanlarında iki çukur bulunan “Meksika şapkası” ile, keskin tepeleriyle öne çıkan Coiflet dalgacığı yer alır. Bu türler, görüntüdeki veya seste oluşan istenmeyen gürültüleri ayıklamakta etkilidir.
Sonuç Olarak
Gördüğünüz üzere dalgacıklar, sinyal ve görüntü analizinde son derece güçlü bir araçtır. Temelde, sinyal analizi gereken her alanda kullanılabilirler. Örneğin:
- Astronomide, gökcisimlerinin en net görüntülerini otomatik olarak seçmekte,
- Adli bilişimde, dijital ses, görüntü ve video dosyalarındaki manipülasyonları tespit etmekte,
- Tıpta ise, kalbe düzensiz kan akışına yol açan kalp hastalıklarını belirlemede işe yararlar. Bu çok yönlülük, dalgacıkları farklı disiplinlerde vazgeçilmez kılar.
Kaynaklar ve ileri okumalar
- How Wavelets Allow Researchers to Transform, and Understand, Data. Yayınlanma tarihi: 13 Ekim 2021. Kaynak site: Quanta Magazine. Bağlantı: How Wavelets Allow Researchers to Transform, and Understand, Data
- Daubechies I (2023) Wavelets: Mathematical Tools for Image Analysis. Front. Young Minds. 11:1200611. doi: 10.3389/frym.2023.1200611
- Usevitch, B. E. 2001. A tutorial on modern lossy wavelet image compression: foundations of JPEG 2000. IEEE Sign. Process. Mag. 18:22–35. doi: 10.1109/79.952803
- Unser, M., and Blu, T. 2003. Mathematical properties of the JPEG2000 wavelet filters. IEEE Trans. Image Process. 12:1080–90. doi: 10.1109/TIP.2003.812329
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel