Fizik, bazıları için sıkıcı ve zorlayıcı olabilir ama her zaman öyle olmak zorunda değildir. Bazen uzaydan Dünya’ya düşen bir hamamböceğine ne olacağını sormak bile fiziksel bir problemdir. Gerçekten de, uzaydan Dünya’ya doğru düşen bir hamamböceği neyle karşılaşır?

Öncelikle “uzay” derken neyi kastettiğimizi açıklamamız gerekir. Bilim insanları da zamanında uzayın nerede başladığı konusunda farklı görüşler ortaya koymuştur. Günümüzde ise, uzayın başlangıcı olarak kabul edilen nokta Karman hattı olarak adlandırılır.
Karman hattı, ortalama deniz seviyesinden 100 kilometre yüksekte bulunan ve Dünya atmosferi ile uzayı ayıran hayali bir sınırdır. Ancak uzayın kesin olarak nerede başladığını söylemek zordur. Çünkü atmosfer bir anda sona ermez; bu nedenle net bir sınırdan söz etmek mümkün değildir. Örneğin NASA ve ABD ordusu, uzayın ortalama deniz seviyesinden 80 kilometre yüksekte başladığını kabul ederken, Fédération Aéronautique Internationale (FAI) bu sınırı 100 kilometre ve biraz üzeri olarak belirler.
Peki Karman hattı nasıl ortaya çıktı? Bu 100 kilometrelik sınır keyfi şekilde mi belirlendi? Hayır. Bu sınır, Macar asıllı havacılık mühendisi Theodore von Karman’ın çalışmaları sonucunda tanımlanmıştır.

Von Karman, havanın kaldırma kuvvetiyle bir uçağın havada kalabilmesi için gereken hızın, hangi yükseklikte yörünge hızını aşacağını merak ediyordu. Burada yörünge hızı, uçağın hiç yere düşmeden Dünya etrafında dönmesini sağlayacak hız anlamına gelir. Karman gerekli hesaplamaları yaptıktan sonra yaklaşık 100 kilometrelik bir sonuç elde etti.
Artık uzayın nerede başladığı konusunda bir fikir birliğine vardığımıza göre, hamamböceğine geri dönebiliriz.
Öncelikle Soruyu Basitleştirelim: Havasız Ortamda Düşen Bir Hamamböceği
Düşen bir cisme en çok etki eden unsur havadır. Bu etki de cismin şekline bağlı olarak değişir. Ancak biz havayı göz ardı edeceğimiz için, hamamböceğinin şekli de önemli değildir. Bu nedenle onu basitçe yuvarlak bir cisim olarak düşünebiliriz. O halde sorumuz şu hâle gelir: Havasız bir ortamda, yerden h kadar yükseklikten bırakılan m kütleli bir cisim, yere ne kadar hızla çarpar?
Eğer bu yuvarlak cismi bir binanın tepesinden bırakıyor olsaydık, yerçekimi ivmesini yaklaşık 9,8 m/s² olarak alabilirdik. Fakat 100 kilometre yükseklikten düşeceği için, yerçekimi ivmesinin bu yükseklikte daha küçük olacağını da hesaba katmamız gerekir. Bu durumu hesaplamak için aşağıdaki formülden yararlanacağız.
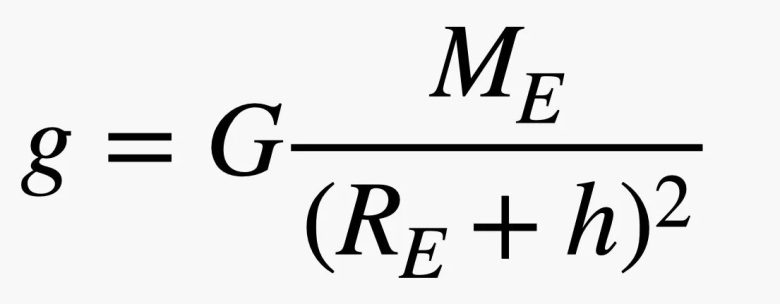
Gerekli hesaplamaları yaptığımızda 100 km yükseklikten Dünya’ya düşen yuvarlak bir cismin 9.49 m/s2 ivmeyle düşeceğini buluruz. Ancak bu yuvarlak cisim sabit olarak bu ivmeyle düşmeyecektir. Dünya’ya yaklaştıkça ivmesi ve dolayısıyla da hızı artacaktır. Peki bunu nasıl hesaplayacağız?
Bunu yapmanın en kolay yolu cismin hareketini birer saniyelik zaman aralıklarıyla incelemektir. Bu 1 saniyelik aralıkların her birinde cismin konumunu ve hızını basit fizikle hesaplayabiliriz. Bunu 100 saniye için yaptığımızda aşağıdaki gibi bir grafik elde ederiz.
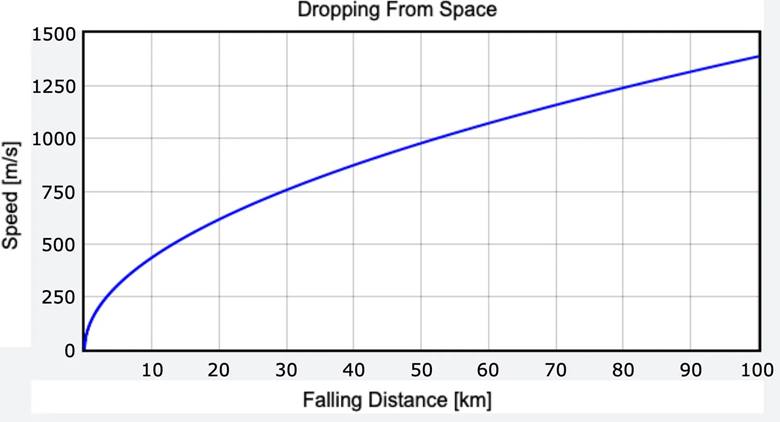
Bu şekilde bir hesaplama yaptığımızda cismin yere saniyede 1389 metre hızla düşeceğini buluruz. Bu hız, en hızlı jet uçağının hızından bile fazladır. Ve çok gerçekçi de değildir. Çünkü hava sürtünmesi cismin bu kadar hızlanmasını engelleyecektir. O halde havanın etkilerini göz önünde bulundurma zamanı gelmiş demektir.
Havanın Olduğu Bir Ortamda Düşen Bir Hamamböceği
Hamamböceğinin havalı bir ortamda düşmesi hava sürtünmesine maruz kalacağı anlamına gelir. Ve bu sürtünme kuvvetini de aşağıdaki formülle hesaplayabiliriz.
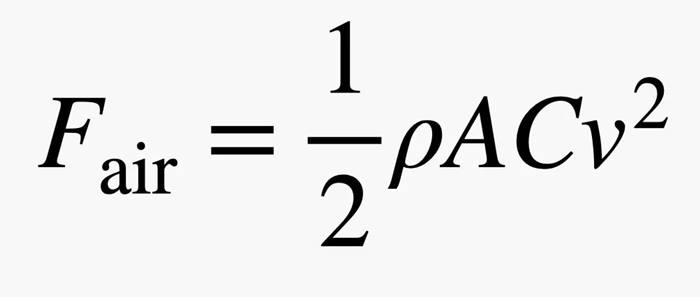
Newton’un ikinci yasasına göre kuvvet hıza, hız da kuvvete bağlı olduğundan problem ilk başta biraz zorlaşıyor gibi gelebilir. Ancak başlangıçta hareketi birer saniyelik zaman aralıklarına böldüğümüz için bu aralıkların her birinde sürtünme kuvvetinin sabit olduğunu varsayabiliriz. Fakat bu problemde değişen tek şey cismin hızı değildir. Havanın yoğunluğu da irtifaya göre değişiklik göstermektedir.
Havasız ortamda düşen bir cismi ele alırken cismin şeklinin önemsiz olduğunu söylemiştik. Fakat havanın olduğu bir ortamda cismin şekli ve boyutu da ne hızda düşeceğine etki eder. Bu yüzden de mesela havalı bir ortamda aşağı düşen bowling ve tenis topları aynı hızda yere düşmeyecektir. Bunu daha iyi anlayabilmek için aşağıdaki grafiği inceleyelim.
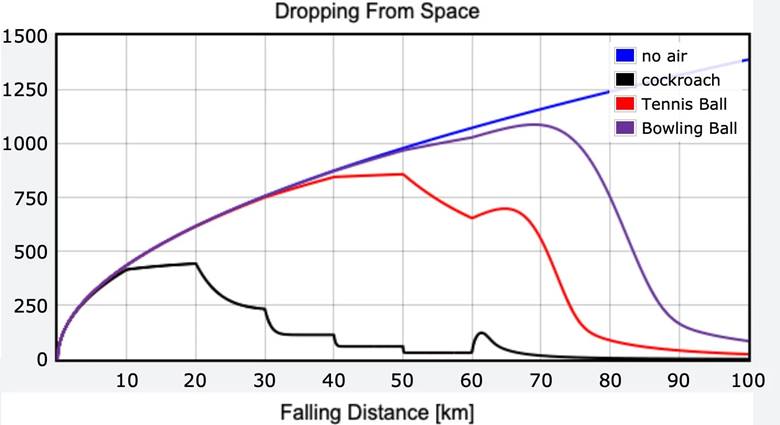
Hava direnci nedeniyle cisimler sonunda terminal ya da limit hız denilen sabit bir hıza ulaşır. Yukarıdaki grafiğe göre bu hız, bowling topu için 83 m/s, hamamböceği için 1,5 m/s, tenis topu için ise 23,8 m/s’dir. Hayatta kalma açısından bakıldığında, saniyede 1,5 metre hızla yere çarpan bir hamamböceğinin hayatta kalması mümkündür. Çünkü hamamböcekleri zaten saniyede yaklaşık 1,3 metre hızla hareket eder. Ancak aynı durum bowling topu için geçerli değildir. Sert bir zemine çarptığında büyük olasılıkla parçalanır.
Ve Bir de Hava Sürtünmesinin Sebep Olduğu Isınma Problemi Var
Bilim kurgu filmlerindeki atmosfere giren göktaşlarından veya uzay araştırmalarından, atmosfere giren yüksek hızlı bir cismin alev aldığını görmüşsünüzdür. Bunun sebebi hızla hareket eden cismin önündeki havayı sıkıştırması ve dolayısıyla da basıncını arttırmasıdır. Basıncı artan bu hava ısınır ve düşen nesnenin ön yüzeyini ısıtır.

Peki bizim hamamböceğimize ne olacak dersiniz? Bizim hamamböceği de göktaşları gibi alev mi alacak? Bu soruları cevaplamak için kaba bir tahmin yapabiliriz. Bunun için de öncelikle hava direncinin yaptığı işi hesaplamamız gerekir. Daha sonra da açığa çıkan ısı enerjisinin yarısının havayı, yarısınınsa hamamböceğini ısıtmak için harcandığını varsayabiliriz.
Bir de hamamböceğinin özgül ısısını hesaplamamız gerekir. Ancak bunu deneysel olarak ölçmekle uğraşmayacağımız için genel bir tahminde bulunacağız.
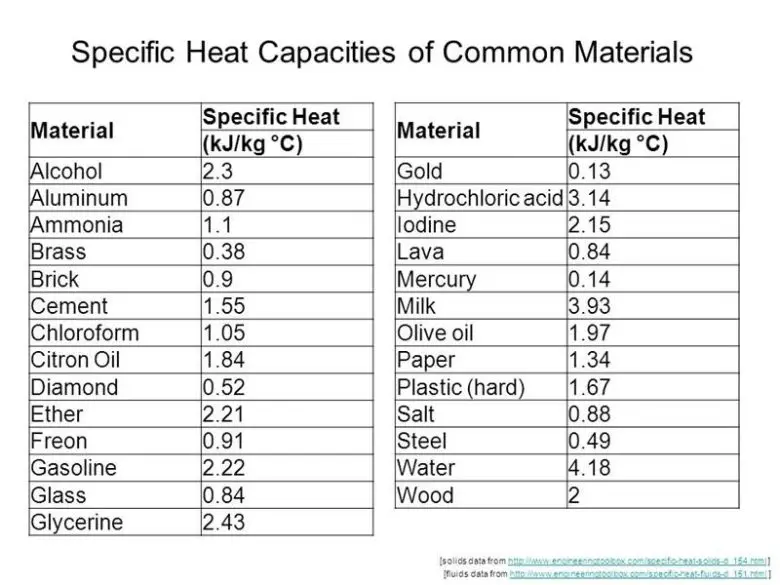
Gerekli hesaplamaları yaptıktan sonra hamamböceğinin 960 santigrat derece gibi bir sıcaklığa ulaşacağını görüyoruz. Eğer bu değer size aşırı geldiyse haklısınız. Çünkü havanın kendisinin cisim üzerindeki soğutucu etkisini hesaba katmadık. Bu soğutma etkisini de hesaba katarsak uzaydan gezegenimize doğru düşen bir hamamböceği düşüşü boyunca ısınmayacaktır. Arada soğuyacak ve bu da onun hayatta kalma şansını arttıracaktır.
Kısacası, bizim hamamböceğinin başına neler geleceği çok kesin bir şekilde bu yazımızda söylemek zor. Çünkü en nihayetinde bu hesaplamaları ve tahminleri bilimsel bir makale için yazmadık. Yine de uzaydan gezegenimize düşen bir hamamböceğinin hayatta kalma şansının olması fiziğin ne kadar ilginç bir bilim olduğunu bize kanıtlıyor.
Kaynaklar ve İleri Okumalar
- Could a Cockroach Survive a Fall From Space? ; Bağlantı: Could a Cockroach Survive a Fall From Space? | WIRED ; Yayınlanma tarihi: 10 Kasım 2023
- The Kármán Line: Where does space begin? ; Bağlantı: The Kármán Line: Where does space begin? | Space ; Yayınlanma tarihi: 14 Kasım 2022
Matematiksel






Harika bir iş yapıyorsunuz.Kutluyorum.Emeklerinize sağlık.