Üçüncü dereceden denklemlerin genel çözümlerinin bulunması hikâyesi, matematik tarihinin en ilginç hikâyelerinden biridir. Hikâye Rönesans İtalya’sında geçer.

Günümüzde pek çok lise öğrencisi ikinci dereceden denklemleri çözmeyi bilir. Örneğin x² − x − 3 = 0 denklemi, standart kök formülüyle kolayca çözülecektir. Peki, daha yüksek dereceli denklemler için buna benzer formüller var mı? Cardano, Tartaglia ve çağdaşlarının temel arayışı buydu.
16. yüzyılda cebir hâlâ sözlü bir dildi. Denklemler sembollerle değil, cümlelerle ifade ediliyordu. Üstelik tüm katsayıların pozitif olması gerekiyordu; çünkü dönemin matematikçileri negatif sayıları meşru kabul etmiyordu. Henüz bilinmeyen bir değişken fikri de yoktu. Bu yüzden x³ + cx = d gibi bir denklem “bir küp ve bazı şeyler bir sayıya eşittir” diye tarif ediliyor, x³ = cx + d ise bambaşka bir problem sayılıyordu.
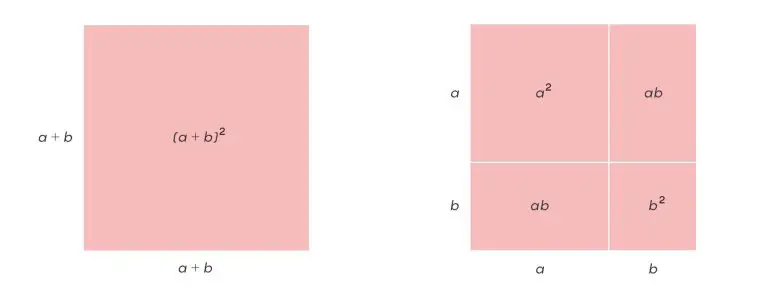
Sembolik cebir olmadan matematikçiler geometrik düşünmek zorundaydı. Örneğin (a + b)² = a² + 2ab + b² ifadesi, o zamanlar şöyle yorumlanırdı: Kenarı a + b olan bir karenin alanı, kenarı a olan bir karenin alanı, kenarı b olan bir karenin alanı ve iki tane a × b dikdörtgenin alanının toplamına eşittir. Aynı yaklaşım küplerde de geçerliydi.
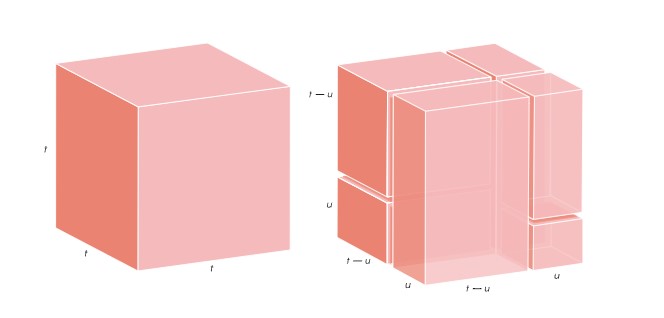
t³ = u³ + (t − u)³ + 2u(t − u) + u²(t − u) + u(t − u)²
(t > u koşuluyla).
Matematik Düellosundan Ortaya Çıkan Formül
Scipione del Ferro, 16. yüzyılın başlarında Bologna Üniversitesi’nde görev yapan bir profesördü ve kübik denklemlerin çözümünde önemli ilerlemeler kaydeden ilk kişi olarak kabul edilir.Ne yazık ki başarılarının tüm detaylarını bilmiyoruz; bunun nedeni, dönemin ilginç akademik gizlilik kültürüdür.
O dönemde, bir teoremi yayımlamak ya da bir problemi çözdüğünü ilan edip bundan doğan itibarı yaşamak yaygın değildi. Bunun yerine matematikçiler, birbirlerine “matematiksel düellolar” ile meydan okurlardı. Zor problemler göndererek rakiplerini sınar, en fazla problemi çözen kişi düellonun galibi olurdu.
Kazanan genellikle mesleki itibar kazanır, daha fazla öğrenci çekerdi. Bu nedenle birçok keşif, ilerideki düellolarda “gizli silah” olarak kullanılmak üzere gizli tutulurdu.
Yine de del Ferro’nun, x³ + cx = d biçimdeki kübik denklemleri çözebildiğini biliyoruz. Bu, özel bir kübik denklem türüdür ve “indirgenmiş kübik denklem” olarak bilinir. Her ne kadar 16. yüzyılın matematikçileri bu denklemleri modern sembollerle ifade etmemiş olsa da, del Ferro bu denklemin köklerinden birinin şu şekilde yazılabileceğini göstermiştir:
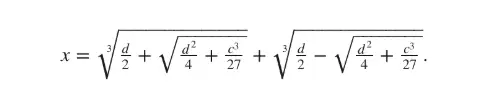
Del Ferro’nun bu özel türdeki denklemleri çözebildiğini şuradan biliyoruz: Tekniğini öğrencisi Antonio Fior’a öğretmişti. Fior da, del Ferro’nun ölümünden sonra bu yöntemi bildiğini övünerek dile getirmişti.
Bu sırada, kendi kendini yetiştirmiş olan Tartaglia, kübik denklemin farklı bir türünü çözmeyi başardı. Bu önemli gelişme, Fior ile Tartaglia arasında matematiksel bir düellonun zeminini hazırladı.

1535 yılında, birbirlerine 30 problem göndererek bir buçuk aylık bir süre tanıdılar. Sürenin dolmasına günler kala, Tartaglia kendisine yollanan denklemlerin çözüm yolunu keşfetti. Fior ise Tartaglia’nın gönderdiği soruların hiçbirini çözemedi. Sonuç olarak Tartaglia’nın zaferi İtalya’da hızla duyuldu; Fior ise büyük bir utançla geri çekildi.
Üçüncü Dereceden Denklemin Genel Çözümü İlk Kim Buldu?
Tartaglia’nın başarısı Cardano’yu etkilemişti. Tartaglia’nın kübik denklemdeki başarısını taklit etmeye çalıştı ama başaramadı. Bunun üzerine Tartaglia’yı yöntemini açıklamaya ikna etmek için baskı kurmaya başladı. Hatta gizlilik yemini etmeyi bile teklif etti.
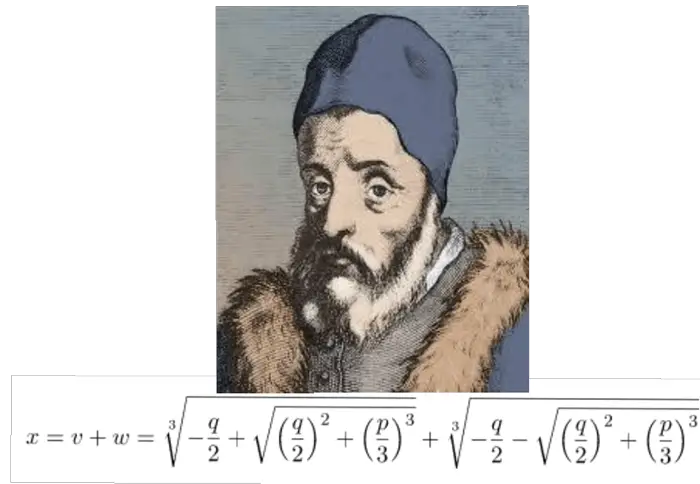
Sonunda, 1539 yılında Tartaglia geliştirdiği yöntemi Cardano’ya açıkladı. Ancak yöntemin neden işe yaradığını gösteren kanıtı paylaşmadı. Yine de bu kadarı Cardano için yeterliydi; kısa sürede tekniğin ardındaki matematiği kendi başına çözdü. Ardından önemli bir gözlem yaptı: x = t − b⁄(3a)
Bu dönüşüm, ax³ + bx² + cx + d = 0 denklemine uygulandığında, denklem t değişkeni üzerinden indirgenmiş bir kübiğe dönüşüyordu. Cardano önce bu yeni denklemi t için çözüyor, ardından bulduğu t değerini dönüşüm formülüne yerleştirerek x’i elde ediyordu. Böylece, herhangi bir kübik denklemin çözülebileceğini gösteren genel bir yöntem geliştirmiş oldu.
Tartaglia’ya verdiği gizlilik yeminine rağmen, Cardano bu sonuçları yetenekli öğrencisi Ludovico Ferrari ile paylaştı. Ferrari, Cardano’nun kübik denklemler üzerine çalışmasına yardımcı olurken cebirde öyle ustalaştı ki, dördüncü dereceden denklemlerin de bir kübiğe indirgenebileceğini keşfetti. Bu sayede, Cardano ve Ferrari dördüncü dereceye kadar olan tüm denklemleri çözebilen ilk matematikçiler oldular.
Cardano, elde ettikleri sonuçları yayımlamak istiyordu. Ancak bu başarılar, Tartaglia’nın kendisine emanet ettiği sırlar sayesinde mümkün olmuştu. Yayımlamak, verdiği yemini bozmak anlamına geliyordu.
1543 yılında, bir seyahati sırasında Cardano, del Ferro’nun defterlerine göz attı ve indirgenmiş kübik denklemi Tartaglia’dan çok daha önce çözdüğünü keşfetti. Cardano’ya göre bu bulgu, artık Tartaglia’ya karşı olan yükümlülüğünü ortadan kaldırıyordu.
İki yıl sonra, Cardano Ars Magna (Büyük Sanat) adlı kitabını yayımladı. Kitapta hem kendi çalışmaları hem de Ferrari’nin kübik ve dördüncü dereceden denklemler üzerine elde ettiği sonuçlar yer alıyordu.
Sonuç Olarak
Tartaglia, Cardano’yu hem hırsızlıkla hem de kutsal bir yemini bozmakla suçladı. Cardano ise tüm suçlamaları sadık yardımcısı Ferrari’nin üzerine yönlendirdi. Aylara yayılan bu tartışma, tarafların birbirine gönderdiği sert ve suçlayıcı broşürlerle sürdü. Gerilim sonunda, Tartaglia ile Ferrari arasında matematiksel bir düelloya, ardından da Ferrari’nin memleketi Milano’da düzenlenen halka açık bir tartışmaya dönüştü.
Tartaglia aslında doğrudan Cardano ile yüzleşmek istiyordu; ancak Cardano bunu reddetti. Ayrıntılar tam olarak bilinmiyor, fakat tartışmanın Tartaglia açısından büyük bir hezimetle sonuçlandığı kesindir. Özellikle coşkulu Milano kalabalığı onun aleyhineydi. Ertesi gün tartışmanın devam etmesi gerekirken, Tartaglia şehri terk etmişti.
Kübik denklemlerin ötesinde kayda değer başarıları olmasına rağmen, Tartaglia yoksulluk içinde ve neredeyse hiç tanınmadan hayatını kaybetti. Cardano ise kalıcı bir ün kazandı. Hatta birçok kişi Ars Magna’nın yayımlanmasını modern matematiğin başlangıcı olarak kabul eder.
Kübik ve dördüncü dereceden denklemlerin çözümünden sonra matematikçiler şu soruyu sormaya başladı: “Daha ne kadar ileri gidebiliriz?” Ancak görünen o ki, çok daha ileri gidilemeyecekti.
Bu gerçeğin ilk kesin kanıtını 1824 yılında, Ars Magna’dan yaklaşık üç yüzyıl sonra, Norveçli matematikçi Niels Abel yayımladı. Ardından, 1830’da henüz 18 yaşında olan Évariste Galois, bu çalışmayı derinleştirdi ve herhangi bir dereceden polinomun çözülebilir olup olmadığını belirleyen kesin kriterleri ortaya koydu.
Galois, iki yıl sonra, bir düelloda hayatını kaybetti (matematik yüzünden değil, gerçek bir silahlı düelloda). Ancak matematiğe yaptığı katkılar, yaşını çok aşan bir miras bıraktı.
Kaynaklar ve ileri okumalar:
- Saiber, Arielle. (2014). Niccolò Tartaglia’s poetic solution to the cubic equation. Journal of Mathematics and the Arts. 8. 10.1080/17513472.2014.933552.
- The Sordid Past of the Cubic Formula. Yayınlanma tarihi: 30 Temmuz 2022. Kaynak site: Quanta Magazine. Bağlantı: The Sordid Past of the Cubic Formula
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





