Tüm negatif ve pozitif tam sayıları toplarsak kaç eder? Diğer bir deyişle tüm tam sayıların toplamı kaçtır? Bu gibi sorular ilk bakışta çok basit görünür. Ancak ardındaki matematik oldukça şaşırtıcıdır.

Pozitif ve negatif tamsayıların sonsuz sayıda olduğunu biliyoruz. Eğer bunların yalnızca sonlu bir kısmını ele alsaydık ve pozitiflerle negatiflerin sayısı eşit olsaydı, toplamları sıfır olurdu. Bu hem sezgisel olarak mantıklıdır hem de matematiksel açıdan doğrudur.
Ancak sonsuzluk devreye girdiğinde işler değişir mi? Bu kafa kurcalayan sorunun peşinden gidip, işin aslını birlikte keşfedelim.
Matematikte Dizi ve Seri Nedir?
Tüm tamsayıları toplamak, ne kolay ne de doğrudan bir işlemdir. Bu nedenle, önce bu işlemin arkasındaki matematiksel süreci anlamamız gerekir. Bu süreci kavramak için de matematikte diziler (sequences) ve seriler (series) kavramlarına aşina olmamız şart.
Bir öğretmen sınav kâğıtlarını topladığında, genellikle onları numara ya da isim sırasına göre dizer. Bu bir dizidir. Yani dizi belli bir kurala göre sıralanmış bir listedir. Günlük hayatımızda buna benzer birçok dizi örneği vardır ve hepsinin ortak özelliği bir örüntü, yani bir desen izlemeleridir.
Matematikte de dizi, belirli bir kurala göre sıralanmış sayıların oluşturduğu listedir. Örneğin, şöyle bir kural düşünelim: ai=i2. Yani dizinin i. terimi, i’nin karesi olsun. Bu kurala göre dizimiz şöyle olur: 1,4,9,16,25,…Gördüğünüz gibi her sayı, kendi sırasının karesidir. Bu da dizinin bir örüntüye göre ilerlediğini gösterir.
Seri dediğimiz şey ise bir dizinin elemanlarının toplamıdır. Yani, bir dizideki sayıları tek tek toplarsak, o dizinin serisini elde ederiz. Örneğin, yukarıda verdiğimiz diziyi hatırlayalım: 1,4,9,16,25,…
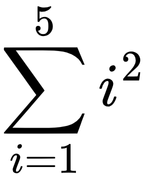
Bu dizinin serisi şöyle olur: 1+4+9+16+25+…Yani her terimi toplayarak ilerleriz. Bu tür toplamlar, matematikte çok önemli bir yer tutar ve sonlu ya da sonsuz olabilir.
Bir Serinin Yakınsak veya Iraksak Olması Ne Anlama Gelir?
Serilerin belirli bir kuralı izleyen dizideki sayıların toplamı olduğunu öğrendik. Ancak daha önce de söylediğimiz gibi, söz konusu dizi her zaman sonlu olmayabilir. Yani sonsuz eleman içerebilir. Örneğin bir önceki bölümdeki Pi = i2 kuralına uyan diziyi sonsuza kadar devam ettirseydik, sonsuz serimizi şu şekilde ifade ederdik:
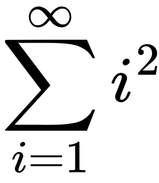
Sizce böyle bir serinin sonlu bir cevabı olabilir mi? Cevap hem evet hem hayır. Ve bu durumun başta sorduğumuz tüm negatif ve pozitif tam sayıları toplarsak kaç eder? sorusunun cevabıyla doğrudan bir ilişkisi vardır.
Sonsuz bir serinin, yani sonsuz sayının toplamının sonucunu bulmak için önce sonlu bir toplam elde etmemiz gerekir. Ardından bu sonlu toplamın, sonsuza giderken nasıl davrandığını incelemek için limitini alırız. Başka bir deyişle, toplamı n tane daha küçük toplama ayırırız ve bu kısmi toplamların limitini alarak serinin toplamına ulaşırız.
Bu yöntemi uyguladığımızda, bazı serilerde toplam belirli bir sayıya giderek yaklaşır. Yani toplama devam ettikçe sonuç, sabit bir değere yakınsar. Bu tür serilere yakınsak seriler denir.
Öte yandan, bazı serilerde toplam hiçbir zaman belirli bir değere yaklaşmaz. Toplam büyüdükçe artmaya devam eder ve sonuç, pozitif ya da negatif sonsuza gider. Bu tür serilere ise ıraksak seriler denir.
O Halde Tüm Negatif ve Pozitif Tam Sayıları Toplarsak Kaç Eder?
Gördüğümüz gibi, tam sayılar belirli bir kurala uyar ve bu yüzden bir dizi oluştururlar. Biz hem pozitif hem de negatif tüm tam sayıların toplamını bulmak istiyorsak, aslında tam sayılar dizisinin serisini, yani toplamını bulmak istiyoruz demektir.
Ancak işte tam da burada işler karmaşıklaşır. Hatırlarsan, tüm toplamı bulmak için kısmi toplamlar kullanıyorduk. Fakat bazı sonsuz serilerde, bu kısmi toplamların sıralanışı ve gruplandırılma şekli nihai sonucu etkileyebilir. Ne yazık ki, tüm tam sayıların (pozitif ve negatif) toplamı da bu türden bir durumdur.
Kısmi toplamları birden fazla şekilde gruplandırabiliriz. Ancak konuyu sade tutmak için sadece iki örnek verelim. Bunlardan ilki aşağıdaki gibidir:
(-1 + 1) + (-2 + 2) + (-3 + 3) + (-4 + 4) + …
Bu şekilde grupladığımızda, her çiftin toplamı 0 eder. Bu durumda, her kısmi toplam 0 olduğu için, toplamın sonucu da 0 olur. Serimiz 0’a yakınsar ve toplamı vardır. Sonuç: 0.
Bu kez sayıları şu şekilde gruplayalım: (-4 + 2) + (-5 + 3) + (-6 + 4) + (-7 + 5) + …Her grupta bir negatif ve bir pozitif sayı var. Ancak seçtiğimiz sayılar öyle ki, her çiftin toplamı -2 ediyor. Bu şekilde devam ettiğimizde, sonsuz tane -2 elde etmiş oluruz. Şimdi kısmi toplamları inceleyelim:
-1. kısmi toplam: -2
-2. kısmi toplam: -4
-3. kısmi toplam: -6
-4. kısmi toplam: -8
-…
Bu şekilde devam ettikçe toplam negatif sonsuza doğru gider. Yani sayı gittikçe küçülür ve hiçbir değere yaklaşmaz. Yani bu seri ıraksaktır ve toplamı yoktur.
Sonuç Olarak
Başlıktaki soruya hem evet hem de hayır demek mümkün; çünkü sonuç, tam sayıların serisini nasıl grupladığımız ve kısmi toplamları nasıl hesapladığımızla doğrudan değişir. Bu durumu açıklamak için daha katı ve matematiksel yöntemler de vardır. Ancak hangi yolu seçersek seçelim, hepsi aynı sonuca götürür.
Kaynaklar ve İleri Okumalar
- If You Add All The Negative Integers With Positive Integers, Would You Get Zero? | ScienceABC ; Yayınlanma tarihi: 19 Ekim 2023
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





