Mühendislerin sıkça paylaştığı ve izleyenleri şaşırtan videolardan biri, havada asılı duran bir masa tasarımıdır. Bu masa, ilk bakışta adeta yerçekimine meydan okuyormuş gibi görünür. Sanki bacakları yoktur ve yalnızca birkaç ince ip tarafından havada tutuluyormuş gibi durur.

Ancak bu görüntü bir göz yanılması değildir — masa gerçekten o şekilde durur. Bu tür yapılar, tamamen fizik kurallarına, özellikle de kuvvetlerin dengesine dayanır. Görünüşte dengesiz gibi görünen bu sistem, aslında oldukça kararlıdır. Bunun arkasındaki temel prensip ise “tensegrity” adı verilen bir yapısal denge sistemidir.
Tensegrity Nedir?
Tensegrity, “gerilim (tension)” ve “bütünlük (integrity)” kelimelerinin birleşiminden oluşur. Yapıda sıkıştırma elemanları (genellikle çubuklar) doğrudan birbirine temas etmez; onları gerilim altındaki kablolar ya da ipler dengede tutar. Bu sistemde her parça görevini yerine getirerek bütün yapının stabil kalmasını sağlar.

Tensegrity terimi ilk olarak efsanevi mimar ve mucit Buckminster Fuller tarafından ortaya atılmıştır. Fuller, alternatif yapı sistemleri üzerine yaptığı deneyler sırasında bu kavramı geliştirmiştir. Tensegrity sistemler, iki temel yapı elemanından oluşur:
- Germe öğeleri (tension elements): Genellikle kablolar, halatlar veya iplerdir. Bu öğeler sürekli gerilim altındadır ve yapının parçalarını birbirine bağlayarak sistemin bütünlüğünü sağlar.
- Basınç öğeleri (compression elements): Genellikle çubuklar veya sert borular şeklindedir. Bu parçalar sıkıştırma kuvveti taşır, ancak birbirlerine doğrudan temas etmezler. Aralarındaki mesafe germe öğeleriyle korunur.
Fuller, yapısal denge ve verimlilik üzerine vizyonunu 1920’lerde geliştirmeye başladı. Bu dönem, birçok tasarımcının ve mimarın geleneksel yaklaşımları sorguladığı ve yeni yapısal çözümler aradığı bir dönemdi. Ancak tensegrity sisteminin ilk fiziksel uygulaması 1949 yılında ortaya çıktı — bu da Fuller’ın öğrencisi ve aynı zamanda bir heykeltıraş olan Kenneth Snelson sayesinde oldu.

Snelson, gergin bir naylon kablo ve havada dengede duran iki X biçimli ahşap çubuk kullanarak ilk tensegrity yapısını oluşturdu. Bu yapı, kendi ağırlığını sadece kablo gerilimi ve çubuklar arasındaki kuvvet dengesi sayesinde taşıyordu. Ne çubuklar birbirine temas ediyordu, ne de yapı bir yere sabitlenmişti. Tamamen kuvvetlerin dengesiyle ayakta duruyordu.
Tensegrity Fikrinin Arka Planındaki Fizik Nedir?
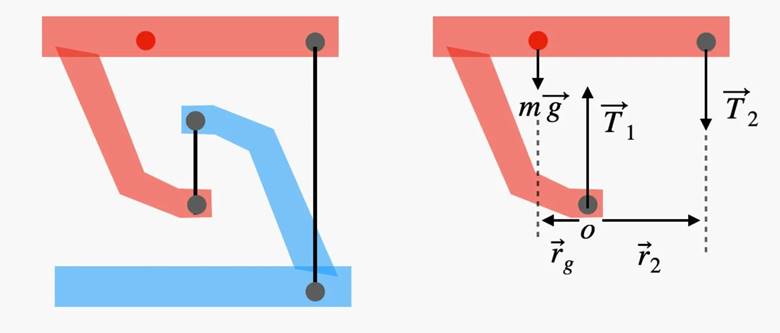
Konuya dair temel kavramları öğrendikten sonra şimdi bu dengenin “yüzen masa” sisteminde nasıl çalıştığını görelim. Bunun için basitleştirilmiş bir diyagramı göz önüne alalım. Bu diyagramda, masa yapısına etki eden üç temel kuvvet göze çarpar.
- Aşağı yönlü yerçekimi kuvveti (mg): Bu, masanın ağırlığını temsil eder. Aslında yerçekimi her noktaya etki eder ama hesaplamalarda bu kuvvetin ağırlık merkezinde toplandığını varsaymak işleri kolaylaştırır. Yani, tüm masanın ağırlığı, ortadaki tek bir noktadan aşağı çekiliyormuş gibi düşünülür.
- ve 3. Yukarı doğru uygulanan iki germe kuvveti (iplerle sağlanan kuvvetler): Bu kuvvetler masanın yan taraflarına bağlanmış olan ipler aracılığıyla uygulanır. İpler gergindir ve masayı yukarı doğru çeker. Aynı zamanda dengeyi sağlamak için belirli açılarla yerleştirilmişlerdir. Masanın havada durmasını sağlayan temel unsur budur.
Eğer bir cisim hareketsizse yani ivmelenmiyorsa, bu cismin dengede olduğunu söyleriz. Fizikte bu durumun gerçekleşmesi için iki temel koşul gerekir:
- Net kuvvet sıfır olmalı: Yani cisme etki eden tüm kuvvetlerin toplamı sıfır vektörüne eşit olmalıdır. Bu, cismin sağa, sola, yukarı ya da aşağı doğru hareket etmemesi için gereklidir. Kısacası, cisim bir yönde sürüklenmiyor ya da düşmüyorsa bu koşul sağlanmış demektir.
- Net tork sıfır olmalı: Herhangi bir referans noktasına göre hesaplanan toplam tork da sıfır olmalıdır. Bu koşul, cismin dönmemesi veya kendi etrafında sabit kalması için gereklidir. Eğer bu şart sağlanmazsa, cisim bir yönde dönmeye başlar.
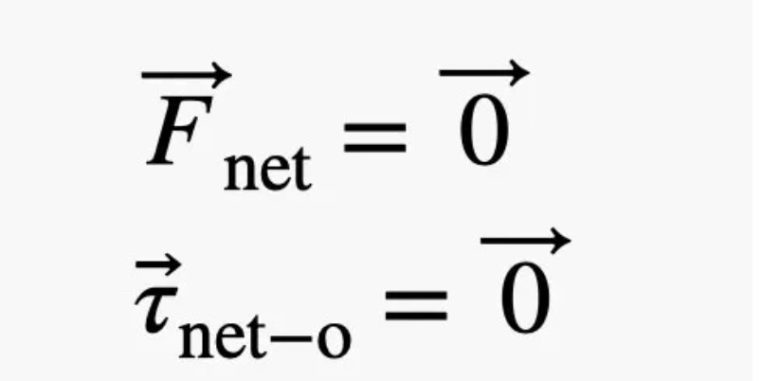
Havada Asılı Duran Bir Masada Tüm Bu Kuvvetler Nasıl Çalışıyor?
Şimdi yüzen masaya geri dönelim. Bu masanın dengede kalması, yani hareketsiz durması gerekiyor. Bu nedenle, üzerine etki eden tüm kuvvetlerin birbirini dengelemesi gerekir. Başka bir deyişle, net kuvvet sıfır olmalıdır.
Bu durumu analiz ederken üç ana kuvvet dikkate alınır. Bu kuvvetlerin tamamı dikey doğrultuda, yani y ekseni boyunca etki eder. Dolayısıyla, yatay yönde (x ekseni) bir kuvvet olmadığı için bu boyutu göz önünde bulundurmamıza gerek kalmaz. Bu da hesaplamaları ve denge analizini daha basit hale getirir.
Bu denklem yalnızca dikey kuvvetlerin dengede olması gerektiğini belirtir. Yani masayı yukarı doğru çeken ip geriliminin, aşağıya doğru etki eden yerçekimi kuvvetiyle diğer aşağı yönlü gerilim kuvvetine eşit olması gerekir. Bu, net kuvvetin sıfır olduğu anlamına gelir ve doğrusal denge koşulunu karşılar. Ancak bu denklem, sistemin dönme eğilimini dikkate almaz.
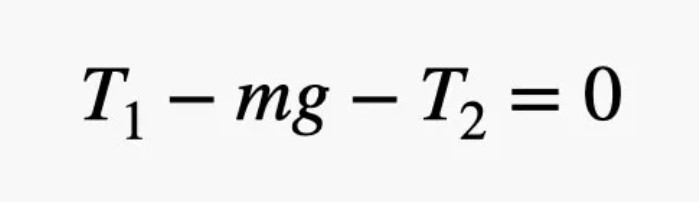
Torku hesaplarken seçtiğimiz nokta oldukça önemlidir çünkü tork, kuvvetin uygulandığı noktanın dönme noktasına olan uzaklığına bağlıdır. Yukarı doğru çeken ipin bağlı olduğu noktayı referans alırsak, bu noktadan geçen herhangi bir kuvvet tork üretmez. Çünkü tork formülü olan τ = F × r ifadesinde, r yani kuvvetin uygulama noktasının dönme noktasına olan uzaklığı sıfırdır. Bu nedenle, bu noktadaki T1 gerilimi tork üretmez.
Ancak diğer kuvvetler—örneğin yerçekimi kuvveti (mg) ya da diğer gerilim kuvveti (T2)—bu noktadan uzak bir yerde etkimektedir. Bu nedenle onlar tork üretir.

T2 sağdan aşağı çektiği için saat yönünde bir tork üretir, yani negatiftir. Yerçekimi de aşağı çeker ama sistemin dengede kalması için ters yönde, yani pozitif bir tork üretmesi gerekir. Bu sadece ağırlık merkezi destek noktasının diğer tarafında olursa mümkündür. Denge tam da bu konum farkı sayesinde sağlanır.
Sonuç Olarak;
Bu yazıda basit bir örnek üzerinden, bu sistemlerin nasıl ayakta durduğunu açıklamaya çalıştık. Gerilimli ipler ve sıkıştırılmış elemanlar birlikte çalışarak yapının sabit kalmasını sağlar. Elbette bu prensibi büyük ve karmaşık yapılara uygulamak, daha hassas hesaplamalar ve mühendislik gerektirir. Ancak sonuç değişmez: Her şey doğru yerleştirilmiş kuvvetlerin dengelenmesiyle ilgilidir.

Günümüzde inşa edilen en dikkat çekici Tensegrity yapılarından biri, Avustralya’nın Brisbane kentinde bulunan Kurilpa Köprüsü’dür. Brisbane Nehri üzerinde yer alan bu yaya köprüsü, mimari ve mühendislik açısından ileri düzey bir örnek oluşturur.
Kaynaklar ve ileri okumalar
- Wait a Second, That Table Has No Legs! Yayınlanma tarihi: 25 Nisan 2020; Bağlantı: https://www.wired.com/s
- 8 Incredible Structures Around the World That Use Tensegrity to Defy Gravity. Yayınlanma tarihi: 2 Ocak 2021; Bağlantı: https://mymodernmet.com/tensegrity-architecture/
- Bansod, Yogesh & Nandanwar, Deepesh & Bursa, Jiri. (2014). Overview of tensegrity – I: basic structures. Engineering Mechanics. 21. 355-367.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel