Alef sayıları, kümeler kuramının temel kavramlarından biridir ve matematiğin çeşitli alanları için geniş kapsamlı sonuçlar doğurur.

Sonsuzluğun doğasını anlamaya çalışırken, çok geçmeden sayılabilir ve sayılamaz kümeler arasındaki farkla karşılaşırsınız. Doğal sayılar sayılabilir bir sonsuzluğu temsil eder. Eğer sınırsız zamanınız olsaydı, hepsini tek tek sayabilirdiniz.
Sonsuz sayıda insandan oluşan bir grup da aynı şekilde sayılabilir bir sonsuzluktur. Yeterince zamanınız olursa bu insanların tümünün isimlerini bir listeye yazar ve tıpkı doğal sayılarda olduğu gibi sırasıyla sayarsınız.
Peki ya sonsuz uzunluktaki bir doğru? O da sonsuz sayıda noktadan oluşur. Ancak bu noktaları da tıpkı doğal sayılar gibi listeleyip sayabilir misiniz?
İlk olarak 0’ı ele alalım. İkinci sayı olarak 0.1’i seçebilirsiniz; ancak 0.01, 0.1’den daha küçüktür ve bu nedenle listede daha önce gelmelidir. Benzer şekilde 0.001, 0.01’den küçüktür. Aslında, hangi sayıyı seçerseniz seçin, ondan daha küçük başka bir sayı her zaman vardır. Bunu yapmak için sadece ondalık noktanın sağına ek sıfırlar koymanız yeterlidir.
Bu nedenle tam bir liste oluşturmak imkânsızdır. Bu durum, sonsuz uzunluktaki bir doğrunun temsil ettiği sonsuzluğun sayılamaz olduğunu gösterir.
Hangi Sonsuzluk Daha Büyük?

Peki, sonsuz bir doğrunun sonsuzluğunun, doğal sayıların sonsuzluğundan “daha büyük” olduğu fikrine ne demeli? Sonlu nesne koleksiyonlarının büyüklüğünü karşılaştırmanın bir yolu — eğer tek tek saymakla uğraşmak istemiyorsanız — onları birebir eşleştirmeye çalışmaktır.
Bir grup sandalye ve bir grup insan düşünün. Her insan için bir sandalye varsa sayılar eşittir; sandalyeler artarsa sandalyeler, insanlar artarsa insanlar fazladır.
Bu fikri sonsuz nesne koleksiyonlarına da genişletebilirsiniz. Eğer A kümesindeki nesneleri B kümesindeki nesnelerle birebir eşleştirebiliyorsanız — A’daki her nesne B’de tam olarak bir nesneye, B’deki her nesne de A’da tam olarak bir nesneye karşılık geliyorsa — o zaman iki koleksiyonun aynı büyüklüğe sahip olduğunu, matematikçilerin deyimiyle aynı kardinaliteye sahip olduğunu söyleriz.
Bu nedenle insan grubu ile doğal sayılar aynı tür sonsuzluğu, yani sayılabilir sonsuzluğu temsil eder. Ancak sonsuz bir doğru üzerindeki noktaları listelemeye çalıştığınızda mutlaka en az bir nokta eksik kalır. Bu yüzden doğrunun kardinalitesi (sayılamaz sonsuzluk), doğal sayıların kardinalitesinden (sayılabilir sonsuzluk) daha büyüktür.
Alef Sayıları İle Tanışın
Evet, sonsuzluk birçok boyutta karşımıza çıkar. 1873’te Alman matematikçi Georg Cantor, sayı doğrusunu dolduran “gerçel” sayıların — çoğu sonsuz basamaklı, örneğin 3,14159… — 1, 2 ve 3 gibi “doğal” sayılardan sayıca fazla olduğunu keşfederek matematiğin temellerini sarstı. Üstelik her iki küme de sonsuz elemandan oluşuyordu.
Doğal sayılar kümesini ve çift sayılar kümesini karşılaştıralım. İlk kümenin daha büyük olduğunu düşünebilirsiniz; çünkü ikinci küme, birincinin yalnızca yarısını içeriyor gibi görünür. Ancak Cantor, iki kümenin elemanlarının birebir eşleştirilebileceğini fark etti.
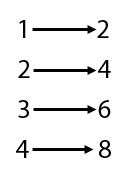
Bu anlamda iki sonsuz küme aynı büyüklüğe sahiptir; Cantor buna “kardinalite” adını verdi ve bu büyüklüğü ℵ₀ (“alef-sıfır”) kardinal sayısıyla gösterdi.
Ancak Cantor, doğal sayıların gerçel sayılarla birebir eşleştirilemeyeceğini de keşfetti. Örneğin 1’i 1,00000… ile, 2’yi 1,00001… ile eşlemeye çalıştığınızda, 1,000000001… gibi sonsuz sayıda gerçel sayı arada kalır. Bunların tamamını saymak mümkün değildir. Bu nedenle gerçel sayıların kardinalitesi doğal sayılarınkinden büyüktür.
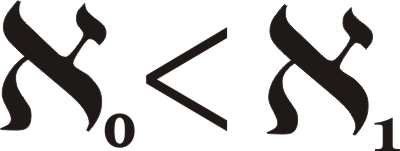
Sonsuzluk boyutları burada bitmez. Cantor, herhangi bir sonsuz kümenin kuvvet kümesinin — yani tüm alt kümelerinin kümesinin — kendi kardinalitesinden daha büyük olduğunu gösterdi. Her kuvvet kümesinin de kendi kuvvet kümesi vardır; böylece kardinal sayılar sonsuz yükseklikte bir sonsuzluklar kulesi oluşturur.
Süreklilik Varsayımı Nedir?
Cantor, sonsuzlukların bu hiyerarşisinde önce en küçük seviyeyi, yani doğal sayıların kardinalitesi olan ℵ₀’ı belirledi. Sonra, doğal sayıların farklı şekilde sıralanmasıyla (örneğin küçükten büyüğe, ya da önce tüm tek sayılar sonra çift sayılar gelecek şekilde) oluşan kümenin, daha büyük bir sonsuzluk seviyesine sahip olduğunu gösterdi. Bu seviyeye ℵ₁ dedi. Bu durumda ℵ₁, ℵ₀’dan “bir kademe daha büyük” bir sonsuzluğu temsil eder.
Cantor, bu ℵ₁ seviyesinin aslında sayı doğrusundaki tüm gerçel sayıların büyüklüğüyle aynı olduğunu düşündü. Buna süreklilik varsayımı (continuum hypothesis) denir. Varsayım şunu söyler: Doğal sayıların sonsuzluğu ile gerçel sayıların sonsuzluğu arasında başka hiçbir “ara büyüklükte” sonsuzluk yoktur; ℵ₁, ℵ₀’dan hemen sonra gelir.
Ancak Cantor, büyük üzüntüsüne rağmen, bunu kanıtlayamadı. 1900 yılında matematikçi David Hilbert, 20. yüzyılda çözülmesi gereken ünlü 23 matematik probleminin listesinde süreklilik varsayımını ilk sıraya koydu.
Sonuç olarak
Gödel, süreklilik hipotezi üzerine 1930 yazında düşünmeye başladı. 1937’de ise hipotezin en azından tutarlı olduğunu gösterdi. Yani, mevcut matematiksel yöntemlerle süreklilik hipotezinin yanlış olduğunu kanıtlayamayız. Devamında Gödel, hipotezin doğru olduğu bir matematiksel model kurdu. Hâlâ süren önemli bir felsefi tartışma var: Cantor’un süreklilik sorusunun cevabı ne? Süreklilik varsayımı gerçekten doğru mu, yoksa yanlış mı?
Kaynaklar ve ileri okumalar:
- What is infinity?; yayınlanma tarihi: 4 Şubat 2015; Bağlantı: https://plus.maths.org/
- How Many Numbers Exist? Infinity Proof Moves Math Closer to an Answer. Yayınlanma tarihi: Kaynak Site: Bağlantı: How Many Numbers Exist? Infinity Proof Moves Math Closer to an Answer.
Matematiksel





