Arthur Conan Doyle’un Sherlock Holmes öyküleri yalnızca edebiyatta değil, matematiğin gelişiminde de önemli bir iz bırakmıştır. Usta dedektifle onun dahiyane düşmanı Profesör James Moriarty’nin hikâyeleri, matematikçi John von Neumann ile ekonomist Oskar Morgenstern’i öyle etkilemişti ki, oyun teorisini geliştirmelerinde rol oynadı.
Von Neumann ile Morgenstern’i özellikle etkileyen, Conan Doyle’un “The Final Problem” adlı öyküsündeki bir sahneydi. Doyle’un öyküsünde Holmes ve Moriarty’nin karşı karşıya kaldığı durum tam da bu türden bir stratejik çatışmadır. Olay örgüsü şu biçimde gelişir.
Sherlock Holmes Ne Yapmalı?
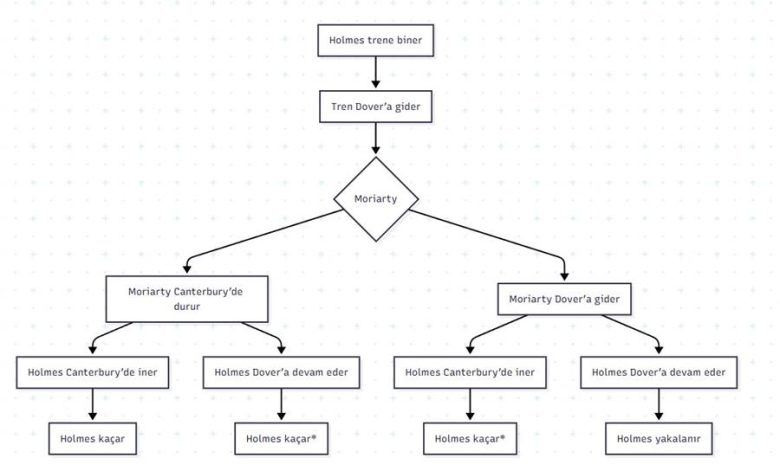
Holmes Dover’a giden trene atlar ve Moriarty trene yetişemez. Bu yüzden tek vagonlu bir motorlu tren kiralayıp peşine düşer. Fakat Holmes’ün treni Dover’a doğrudan gitmez; yol boyunca Canterbury’de bir mola verir. Böylece Moriarty kritik bir kararın eşiğine gelir. Canterbury’de durup Holmes’ün orada inmesini mi beklemelidir, yoksa hiç durmadan Dover’a kadar devam mı etmelidir?
Holmes de kendi yolculuğunu buna göre planlamak zorundadır. Dover’a giderse Avrupa’ya kaçma şansı vardır. Ancak Moriarty’nin bunu öngörüp Dover’da pusuya yatması da muhtemeldir. O zaman Holmes Canterbury’de inmelidir. Fakat Moriarty’nin de onun bu ihtimali hesaplayıp Canterbury’de beklemesi de mümkündür. İki tarafın da almak zorunda oldukları kararlar aşağıdaki gibi özetlenebilir.
John von Neumann ve Oskar Morgenstern, 1944’te yayımladıkları kitapta bu sahneden yola çıkarak stratejik karar verme sorunlarını inceledi ve şu sonuca vardı. “Holmes, treni Victoria İstasyonu’ndan ayrıldığı anda yüzde 48 oranında ölü sayılmalıdır.”
Stratejik Düşünme ve Minimax İlkesi
Holmes ile Moriarty’nin karşı karşıya geldiği bu durumda temel sorun, iki tarafın da birbirinin ne düşüneceğini tahmin etmeye çalışmasıdır. Kkarşılıklı akıl yürütme zinciri, Holmes’ü çıkmaz bir döngüye sokar. Bu yüzden Holmes, Moriarty’nin hangi seçeneği seçerse seçsin bunu öngöreceğini varsaymalı ve kendisini en kötü senaryoya göre koruyacak bir karar vermelidir.

Von Neumann’ın 1928’de ortaya koyduğu temel strateji tam olarak bunu söyler. Bir oyuncu, rakibinin verebileceği en büyük zararı vermeye çalıştığını varsayarsa kendi kazancını en iyi hâle getirebilir. Bu yaklaşım “en küçük kaybı maksimize etme” (minimax) stratejisidir.
Taş–kâğıt–makas oyununu düşünün. Bir oyuncu düzenli davranmaya başladığında rakip bu düzeni fark eder ve onu yenmeye başlar. Bu nedenle en iyi çözüm, taş, kâğıt ve makası eşit olasılıkla, yani her birini üçte bir ihtimalle seçmektir. Böyle yapıldığında uzun vadede iki taraf da aynı oranda kazanır ve kaybeder. Yani zarar en aza iner.
Holmes’ün durumunda da benzer bir mantık geçerlidir. Mantıklı olan, Moriarty’nin saldırısını en kötü ihtimale göre varsaymak ve kararını buna göre vermektir. Bu nedenle yapılan seçimde en güvenli yol, kararın tamamen tahmin edilemez hâle getirilmesidir. Böylece Moriarty’nin üstünlük kurma şansı da azalmış olur.
Sherlock Holmes Ne Yapmalı?
Durumu anlamanın en iyi yolu, olası senaryoların her birine sayısal bir değer vermektir. Neumann ve Morgenstern –100 ile 100 arasında değişen puanlar kullandı. Yüksek değerler bir oyuncu için avantajı, düşük değerler ise kaybı ifade ediyordu. Dört olası durum vardı.
- Hem Holmes hem de Moriarty Dover’a gider. Moriarty Holmes’ü orada öldürür. Bu Moriarty için en iyi sonuç olduğu için değeri 100’dür. Holmes için de –100 olur.
- Moriarty Canterbury’de iner, Holmes Dover’a devam eder. Holmes izini kaybettirebilir. Bu Moriarty için –50, Holmes için +50 değerindedir.
- Moriarty Dover’a gider, ama Holmes Canterbury’de inmiştir. Bu Moriarty için kötü bir durumdur ama bir önceki kadar da yıkıcı değildir. Bu nedenle 0 olarak kabul edilir.. Holmes için de durum nötrdür, çünkü hâlâ İngiltere’dedir.
- İki taraf da Canterbury’de iner. Bu Moriarty için en iyi ikinci sonuçtur ve 100’dür. Holmes için yine ölüm anlamına gelir; değeri –100’dür.
| Senaryo | Holmes’in Kararı | Moriarty’nin Kararı | Moriarty’nin Değeri | Holmes’in Değeri |
|---|---|---|---|---|
| 1 | Dover’a gider | Dover’a gider | 100 | –100 |
| 2 | Dover’a gider | Canterbury’de iner | –50 | +50 |
| 3 | Canterbury’de iner | Dover’a gider | 0 | 0 |
| 4 | Canterbury’de iner | Canterbury’de iner | 100 | –100 |
Her iki taraf da kendi getirilerini maksimize etmeye çalışır. Ancak belirgin bir kazanan strateji yoktur. Bu nedenle tek çözüm şansa başvurmaktır.
Holmes ve Moriarty’nin Canterbury ya da Dover arasında seçim yaptığını düşünelim. Tercihlerinde yazı–tura gibi bir rastlantı mekanizması kullandıklarını varsayalım. Moriarty’nin Canterbury’de durduğunu kabul edelim ve Holmes’ün beklenen getirisini hesaplayalım.
Holmes Dover’a devam ederse iyi ve kötü sonuçların olasılığı eşittir. Bu durumda beklenen değeri: 0,5 × 50 – 0,5 × 100 = –25. Holmes Canterbury’de inerse durum daha kötüdür: –0,5 × 100 + 0,5 × 0 = –50
Holmes’ün toplam beklenen getirisi böylece –37,5 olur. Moriarty’nin beklenen getirisi ise aynı büyüklükte, fakat ters işaretlidir. Bu analiz, Holmes’ün her seçenekte belirli bir risk altında olduğunu ve onu koruyan tek stratejinin davranışını rastlantısal hâle getirmek olduğunu gösterir.
Oyun Teorisi Sherlock Holmes İçin Ne Önerir?
Holmes ve Moriarty yazı–tura ile karar verdiğinde her seçenek eşit olasılıktaydı. Ancak yazı tura atmak yerine olasılıkları farklı biçimde dağıtacak bir yöntem seçersek işler değişebilir.
Holmes’ün Dover’ı seçme olasılığının p, Moriarty’nin Dover’ı seçme olasılığının ise q olduğunu varsayalım. Böylece iki tarafın Canterbury’ye gitme olasılığı sırasıyla 1 – p ve 1 – q olur.
- Moriarty Dover’a giderse Holmes’ün beklenen getirisi: –100 × p olur.
- Moriarty Canterbury’de inerse Holmes’ün getirisi: 50 × p – 100 × (1 – p) = 150p – 100’dür.
İlk durumda Holmes’ün getirisi p arttıkça düşer; ikinci durumda ise artar. Holmes en kötü duruma hazırlanmak için her iki getirinin eşit olacağı p değerini seçmelidir. Yani: 150p – 100 = –100p
Bu denklemi çözdüğümüzde p = 0,4 çıkar. Holmes’ün Dover’a gitme olasılığı %40, Canterbury’de inme olasılığı ise %60 olmalıdır. Aynı mantık Moriarty için de geçerlidir. Hesaplandığında q = 0,6 bulunur. Yani Moriarty Dover’a %60 oranında gitmelidir.
Bu durumda Holmes’ün hayatta kalma olasılığı iki ihtimalin toplamından oluşur. Holmes Dover’a giderse hayatta kalması için Moriarty’nin Canterbury’ye gitmiş olması gerekir. Bunun olasılığı 0,4 × 0,4’tür. Holmes Canterbury’de inerse bu kez Moriarty’nin Dover’a gitmiş olması gerekir. Bunun olasılığı da 0,6 × 0,6’dır.
İki olasılığı topladığımızda: 0,4 × 0,4 + 0,6 × 0,6 = 0,52 elde ederiz. Yani Holmes’ün yaşama ihtimali yüzde 52’dir. Bu oran, yazı–tura ile karar verilen senaryoya göre biraz daha yüksektir.
Sonuç olarak
Böylece von Neumann ve Morgenstern, Holmes’ün karşı karşıya olduğu çıkmazı matematiksel olarak çözmüş oldular. Peki hikâyede ne olur?

Holmes ve Moriarty yazı–tura atmaz. Ama yine de sezgileri onları oyun teorisinin öngördüğü yönde davranmaya iter. Holmes Canterbury’de trenden iner. Moriarty ise tek vagonlu motorlu aracıyla Dover’a doğru ilerlemeyi sürdürür ve Holmes’ün onu alt ettiğinden habersizdir.
Doyle’un bu çözümü seçmesi dikkat çekicidir; çünkü o dönemde oyun teorisi henüz ortaya çıkmamıştı ve bu sonucun matematiksel olarak en iyi strateji olduğunu bilmesi mümkün değildi. Bu belki bir rastlantıydı, belki de güçlü sezgelerinin doğal bir sonucuydu. Ne olursa olsun, Holmes hikâyelerinin hâlâ okunmaya değer olduğunu bir kez daha hatırlatıyor.
Kaynaklar ve ileri okumalar
The Game Theory Hidden in the Mind of Sherlock Holmes. Kaynak site: Scientific American. Yayınlanma tarihi: 24 Temmuz 2025. Bağlantı: The Game Theory Hidden in the Mind of Sherlock Holmes
Matematiksel






