Tek başına kaybettiren iki oyunu bir araya getirirseniz, ortaya kazandıran bir strateji çıkabilir. Parrondo Paradoksu olarak isimlendirilen bu durum yalnızca bir matematiksel tuhaflık değil; bilimsel olarak da önemlidir.

Parrondo Paradoksunu anlamak için iki basit oyunu hayal edelim. İlk oyun, A oyunu, bir madeni para atışıyla oynansın. Ancak bu para tam dengeli değil; bir yüzü %50,5 olasılıkla geliyor.
Kural şu: Para o yüzde 50,5’lik yüzüne gelirse ben kazanıyorum, diğerine gelirse sen kazanıyorsun. Eğer kazanırsan ben sana 1 dolar veriyorum, kaybedersen sen bana 1 dolar veriyorsun.
Bu oyunu defalarca oynarsan uzun vadede ortalama her elde bir sent kaybedersin. Çünkü ortalama kazancın 0.495 – 0.505 = –0.01’tir. Yani A oyunu küçük ama sürekli bir kayıp getirir.

İkinci oyun, B oyunu, biraz daha karmaşıktır. Bu oyunda iki farklı şans çarkı var. Hangi çarkı çevireceğin, elindeki paraya bağlıdır. Eğer o sırada sahip olduğun para 3’e tam bölünüyorsa, yalnızca %9,5 kazanma şansı veren çarkı çevirirsin. Fakat paran 3’e bölünemiyorsa, bu kez %74,5 kazanma olasılığı olan çarkı çevirirsin.
B oyunu da tıpkı A gibi 1 dolarlık bahisle oynanıyor. Ancak bu kez ortalama olarak her elde 87 sent kaybediyorsun. Örneğin 9 doların varsa, bu miktar üçe tam bölündüğü için kötü çarkı çeviriyorsun ve büyük olasılıkla kaybediyorsun. Elinde 8 dolar kalıyor. Sonraki elde 8 üçe bölünemediği için bu kez iyi çarkı çeviriyorsun ve kazanma olasılığın yükseliyor. Böylece paran tekrar 9 dolara dönüyor.
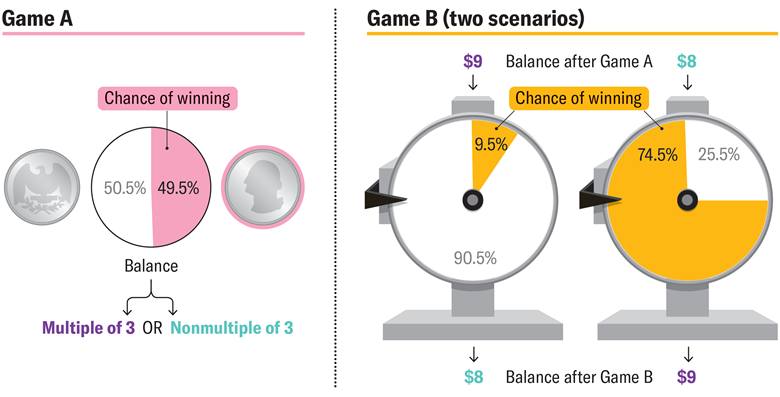
Bu döngü nedeniyle, sahip olduğun paranın üçe bölünebilir olma durumu beklenenden daha sık gerçekleşiyor. Yani ortalama olarak düşündüğünde kötü çarkı, sandığından daha fazla çeviriyorsun. Markov zinciri adı verilen olasılık yöntemiyle yapılan hesaplamalar, B oyunundaki genel kazanma olasılığının yalnızca %49,565 olduğunu gösteriyor. Yani her elde ortalama 0,0087 dolar kaybediyorsun.
Parrondo Paradoksu Nedir?
Sonuçta hem A hem de B oyunu tek başına kaybettiriyor. Ama şaşırtıcı biçimde, bu iki oyunu belirli bir sırayla karıştırarak oynadığında, toplam sonuç kazançlı hale geliyor. İşte Parrondo paradoksu tam olarak bunu anlatıyor: İki kaybettiren strateji birleştiğinde kazandırabilir.
Akılcı bir oyuncu, A ya da B oyunlarından hiçbirine katılmazdı. Sonucunda her iki durumda da uzun vadede kaybedersin. Ancak Juan Parrondo şaşırtıcı bir şey fark etti: Bu iki kaybettiren oyunu belirli bir sırayla oynarsan, toplamda kazançlı çıkarsın.
Örneğin her seferinde iki kez A oyununu, ardından iki kez B oyununu oynarsan, ortalama olarak tur başına 1,48 sent kazanırsın. Ya da her A oyununu iki B oyunu izlerse, bu kazanç 5,8 sente çıkar.
Yani her iki durumda da uzun vadede kâr edersin. Daha da ilginci, A ve B oyunlarını hangi sırayla oynayacağına rastgele karar versen bile (örneğin adil bir para atışıyla), yine kazanç elde edersin. Bu durumda ortalama kazancın tur başına 1,47 sent olur.
Peki bu nasıl mümkün olur? Parrondo paradoksunun özü burada yatar. Oyun B, elinde bulunan paraya bağlıdır; o para miktarı da oyun A’daki kazanma veya kaybetme durumlarına göre değişir. Yani A ve B artık birbirinden bağımsız değildir, birbirini etkiler.
Bu etkileşim sayesinde iki kaybettiren strateji birleştiğinde kazandıran bir sisteme dönüşür. Eğer oyun B, örneğin hangi çarkı çevireceğini belirlemek için zar atmaya dayansaydı, bu bağlantı ortadan kalkar ve paradoks da yok olurdu.
Parrondo Paradoksu Neden Önemlidir?
1996’daki keşiften bu yana, Parrondo paradoksu üzerine pek çok araştırma yapıldı. 2017’de iki bilgisayar bilimci, bu paradoksun balçık mantarlarının yaşam stratejilerini açıklayabileceğini gösterdi.
Bu canlılar bazen tek başına, bazen de koloni hâlinde yaşar. Yalnız yaşam uzun süre sürdürülemez; koloni yaşamı ise çevreyi tüketir. İki stratejiden biri tek başına başarısız olurken, dönüşümlü biçimde uygulanmaları hayatta kalmayı sağlar.
2025’te Çin’in Lanzhou Üniversitesi’nden hesaplamalı fizikçi Jian-Yue Guan ve ekibi, paradoksun tıpta da kullanılabileceğini öne sürdü. Kanser tedavisinde genellikle iki kemoterapi yaklaşımı uygulanır: ya belirli aralıklarla yüksek dozlar verilir ya da sürekli düşük dozda ilaç uygulanır. Birincisinde tümör hücreleri direnç kazanabilir; ikincisinde ise ilaç dozu yeterli olmaz.
Bilgisayar simülasyonları, bu iki yöntemin belirli aralıklarla dönüşümlü kullanılmasının daha iyi sonuçlar verebileceğini gösterdi. Bu yaklaşımın kanser tedavisinde gerçekten işe yarayıp yaramayacağı henüz bilinmiyor, ancak Guan ve ekibi laboratuvar ortamında bu fikri test etmeyi planlıyor.
Yazının devamında göz atmak isterseniz: 100 Mahkum Problemi: Cevabını Bilseniz Bile İmkânsız Gibi Gelen Bilmece
Kaynaklar ve ileri okumalar
- Liu DM, Liu YY, Wu ZX, Guan JY. Parrondo’s paradox in tumor ecosystems: Adaptive therapy strategies to delay the development of drug resistance. Phys Rev E. 2025 Aug;112(2-1):024404. doi: 10.1103/xjh4-mfvx. PMID: 40954788.
- Harmer, G., Abbott, D. Losing strategies can win by Parrondo’s paradox. Nature 402, 864 (1999). https://doi.org/10.1038/47220
- A Mathematical Paradox Shows How Combining Losing Strategies Can Create a Win. Yayınlanma tarihi: 16 Ekim 2025. Kaynak site: Scientific American. Bağlantı: A Mathematical Paradox Shows How Combining Losing Strategies Can Create a Win
Matematiksel