2000 yılında Clay Matematik Enstitüsü, çözülememiş yedi büyük matematik problemi için her birine 1 milyon dolarlık ödül koydu. Ancak içlerinden biri, bu miktardan çok daha fazlasını hak ediyor olabilir: P ve NP problemi.

Bilgisayar biliminin en büyük bilinmezi olan bu soruya doğru bir cevap verilirse, sonuçları milyon dolarlık değil, belki de milyarlarca dolarlık olacaktır. Çünkü eğer bu problem çözülürse:
- Diğer altı Milenyum Problemi de mekanik olarak çözülecektir. Eğer P = NP ise, bu problemleri çözmek için gereken kanıtları bulmak da algoritmik olarak mümkün olur.
- Mevcut tüm çevrimiçi güvenlik sistemleri çöker. Şifreleme yöntemlerinin çoğu, bazı problemleri çözmenin “zor” olduğuna dayanır. P = NP olursa, bu “zor” problemler bir anda kolaylaşır.
- Bilim devrim geçirir. Protein katlanmalarından hava durumu simülasyonlarına kadar, çok fazla hesaplama gerektiren işler aniden yapılabilir hâle gelir.
Bu nedenle, “P ve NP problemi” sadece matematiksel bir merak değil. İnterneti, ekonomiyi, bilimi ve hatta toplumu derinden sarsabilecek bir meseledir.
P ile NP Nedir?
P ve NP problemi, bir çözüm bulmakla o çözümün doğruluğunu kontrol etmek arasındaki farkı sorgular. Örneğin, yeni kitabınızı tanıtmak için bir dünya turu planladığınızı düşünün. Farklı rotalar deniyorsunuz ama her seferinde bütçenizi aşıyorsunuz. Ne yazık ki, şehir sayısı arttıkça denenecek rota sayısı da üssel biçimde artar. Kısa sürede tüm olasılıkları tek tek kontrol etmek bilgisayarlar için bile olanaksız hâle gelir.
Tam o sırada menajeriniz size bir uçuş listesi gönderir. Rotanın bütçeye uygun olup olmadığını anlamak için sadece her şehre uğrayıp uğramadığını kontrol eder, bilet fiyatlarını toplarsınız. Gördüğünüz gibi, çözüm bulmak zorken verilen çözümü doğrulamak oldukça kolay.
P ve NP sorusu tam olarak şunu sorar. Eğer bir çözümü hızlıca doğrulayabiliyorsak, acaba onu bulmak da aynı derecede kolay olabilir mi? Belki milyarlarca seçeneği denemek yerine, işi kestirmeden çözecek bir yol vardır. Örneğin, menajeriniz sizden sadece iki uzak havaalanı arasında bütçeye uygun bir rota bulmanızı isteseydi, bu da zor görünebilirdi. Ama bu tür problemler, bilgisayar bilimcilerinin geliştirdiği hızlı algoritmalar sayesinde kısa sürede çözülebiliyor.

Teorik bilgisayar biliminin bir alt dalı olan karmaşıklık kuramında (complexity theory), araştırmacılar bilgisayarların belirli türdeki problemleri ne kadar kolay çözebildiğini anlamaya çalışır. P, bilgisayarların verimli (yani makul sürede) çözebildiği problemleri temsil eder.
NP ise, bilgisayarların bir çözümün doğru olup olmadığını verimli şekilde doğrulayabildiği problem sınıfıdır. Kitap turu örneğimiz, akademik adıyla Gezgin Satıcı Problemi (Traveling Salesperson Problem), NP sınıfına girer çünkü bir çözüm verildiğinde, bu çözümün işe yarayıp yaramadığını hızlıca kontrol edebiliriz.
“P = NP” Sorusu Nedir?
Burada dikkat edilmesi gereken bir nokta var: P, aslında NP’nin bir alt kümesidir. Çünkü bir problemi doğrudan çözmek, zaten o çözümün doğruluğunu da göstermektir. Örneğin, 27 x 89 = 2.403 ifadesinin doğru olup olmadığını kontrol etmek isterseniz, çarpma işlemini kendiniz yaparsınız ve sonucu karşılaştırırsınız. Bu, çözümle doğrulamanın örtüştüğü durumlardan biridir.
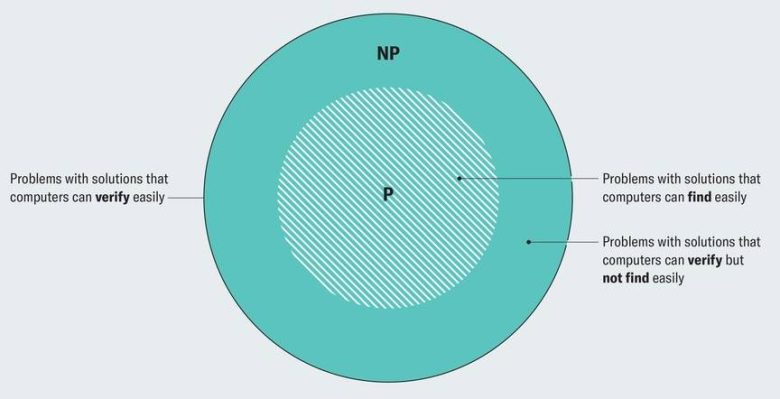
Bu ilişkiyi genelde basit bir Venn diyagramıyla gösteririz: P, NP kümesinin içinde yer alır. Ancak asıl soru şudur. P ve NP gerçekten farklı kümeler mi, yoksa aslında aynı küme mi? İşte bu, P ≠ NP mi yoksa P = NP mi sorusudur — ve bilgisayar biliminin en büyük gizemlerinden biridir.
NP sınıfında olup da P sınıfında olmayan bölgede yer alan problemler, şu anda bilinen hiçbir verimli algoritmayla çözülemeyen sorunlardır. Ancak bu durumun nedeni kesin değildir. Belki bu problemler için gerçekten verimli algoritmalar yoktur ya da belki de biz henüz yeterince zeki bir çözüm yolu bulamadık. İşte NP sınıfında olup da P sınıfında yer aldığı bilinmeyen bazı problem örnekleri:
- Bir sosyal ağda, birbirini tanıyan belirli sayıda kişiden oluşan bir grup var mı?
- Genelleştirilmiş n x n sudoku bulmacasının bir çözümü var mı?
- Bir haritada ülkeleri, komşu ülkeler farklı renklerde olacak şekilde yalnızca üç renkle boyamak mümkün mü?
Bu sorulara verilen çözümleri doğrulamak genelde kolaydır. Ancak çözümü bulmak çok daha zordur. Ayrıca küçük boyutlu örnekleri çözmek ya da yaklaşık çözümler üretmek yeterli değildir. Gerçek bir çözüm, her durumda işe yarayan eksiksiz bir algoritma gerektirir.
Bu problemler, tüm olasılıkları tek tek deneyip kontrol eden brute-force aramayla çözülebilir. Ancak olasılıkların sayısı problem boyutuyla birlikte üstel olarak artar. Eğer problemi tanımlayan büyüklüğe “n” dersek, kontrol edilmesi gereken durum sayısı genellikle 2ⁿ şeklindedir. Günümüzün en hızlı süper bilgisayarları bile böyle bir artışa karşı koyamaz.
P ile NP Birbirine Eşit Olursa Ne Olur?
Binlerce başka NP problemi daha vardır. Hücre biyolojisinden oyun teorisine kadar, P vs NP sorusu bilimin ve endüstrinin her alanına uzanır. Eğer P = NP çıkarsa, yani tüm NP problemleri verimli algoritmalarla çözülürse, dijital ekonomi tamamen çökecektir.
Çünkü kredi kartı bilgileri, şifreler gibi özel verileri koruyan şifreleme sistemleri, yalnızca “zor” problemlerin çözülmesinin gizli anahtar olmadan mümkün olmamasına dayanır. Bu sistemlerin güvenliği, henüz kanıtlanmamış matematiksel varsayımlar üzerindedir. P = NP olduğu anda bu varsayımlar geçersiz kalır.
İlginç bir şekilde, matematik de NP sınıfına dahil edilebilir çünkü bilgisayarlar, matematiksel kanıtları doğrulamayı verimli bir şekilde yapar. Ünlü matematikçi Kurt Gödel, 1956’da John von Neumann’a yazdığı bir mektupta P vs NP problemini dile getirmiş ve eğer P = NP ise, “bir matematikçinin zihinsel çalışmasının bir makineyle tamamen değiştirilebileceğini” söylemişti.
Sonuç olarak
Eğer bir matematikçiyseniz ve işinizi kaybetmekten korkuyorsanız rahat olun. Çoğu uzman, P ≠ NP olduğuna inanıyor. Çünkü çözüm bulmanın her zaman doğrulamadan daha zor olabileceğine dair sezgisel bir inanç var. Ayrıca, P içinde olduğu bilinmeyen en zor NP problemlerine yıllardır kimse verimli bir çözüm bulamadı. Oysa bu problemler ün ve ödül vaat ediyor.
Yine de, sezgiler ve karşı örnek eksikliği bir kanıt sayılmaz. P ≠ NP olduğunu ispatlamak, bu sınıfa ait her zor problem için hiçbir verimli algoritmanın var olmadığını göstermek demektir. Ancak bu görev günümüz matematik teknikleriyle oldukça zor gibi.
Kaynaklar ve ileri okumalar:
- An extremely superficial look at some complexity classes. Yayınlanma tarihi: 25 Ocak 2018; Bağlantı: An extremely superficial look at some complexity classes
- P vs. NP – The Greatest Unsolved Problem in Computer Science. Kaynak site: Quanta Magazine. Bağlantı: P vs. NP – The Greatest Unsolved Problem in Computer Science
- The Most Important Unsolved Problem in Computer Science. Yayınlanma tarihi: 22 Aralık 2023. Bağlantı: The Most Important Unsolved Problem in Computer Science
Matematiksel





