Saçınıza şampuan sürdüğünüz anda sular kesilir. Ailecek pikniğe gitmeye kalkarsanız, kapının dışına çıktığınız anda yağmur yağar. Trafikte adım adım ilerlerken diğer tüm şeritlerin daha hızlı hareket ettiğini görürsünüz. Şerit değiştirirsiniz ama bu sefer siz beklerken, diğer şeritler hızla akmaya başlar. Sanki tüm dünya size karşı gelmiş gibi hissedersiniz. Murphy Kanunları dünyasına hoş geldiniz.
“Bir şeyin ters gitme olasılığı varsa, ters gidecektir. Üstelik bu olası en kötü zamanda gerçekleşecektir.” diyen Murphy kanunu hakkında muhtemelen bugüne kadar çok şey duydunuz. Ancak Murphy kanunu gerçek mi? Yoksa karamsar zihinlerimizin bir uydurması mı? diye merak ediyorsanız okumaya devam ediniz. Ancak öncelikle bu kanunların hayatımıza nasıl girdiğine göz atalım.
Murphy Kanunu Nereden Çıktı?
Yıllarca birçok kişi, insanın ses hızından daha hızlı uçmaması gerektiğine karar verdi. Bu durum, uçakların hızlanmasını kısıtlayan bu engeli aşma arayışını teşvik etti. Sonucunda bu düşüncenin yanlış olduğu anlaşılacaktı. Bell X-1 adı verilen uçak 14 Ekim 1947’de ses duvarını aştı.
Ancak Kaliforniya’daki Edwards Hava Kuvvetleri Üssü’ndeki mühendisler daha da hızlı gidebileceklerini biliyorlardı. Öte yandan buna insan vücudunun nasıl tepki vereceğini bilemiyorlardı. Sonucunda bir insanın G kuvvetine ne kadar dayanabileceğini görmek için MX981 projesini başlattılar.
Bu proje kapsamında gönüllü denekler üzerinde çeşitli testler uygulanacaktı. Bu deneklerden birisi de Hava Kuvvetleri’nde bir doktor olan Albay John Paul Stapp idi. Bu testlerin elbette güvenlik kontrollerinden geçmesi gerekiyordu ve bu kontrollerden sorumlu kilit kişilerden biri, Edward A. Murphy, Jr. adlı bir mühendis idi.
Aslında hikayenin devamı kaynaklarda değişiklik göstermektedir. Ancak genel hikaye şu biçimdedir. Dr. Stapp’ın dahil olduğu G kuvveti testi esnasında bazı sensörler kullanılması gerekiyordu. Ancak, ilk test sırasında, sensörler sıfır değerini gösterdi ki bunun olması mümkün değildi.
Sorunu anlamak için inceleme yapan Murphy, yanlış bağlandıkları için 16 göstergenin hepsinin aynı anda arızalandığını tespit etti. Sensörleri bağlamanın yalnızca iki yolu vardı ve her biri de bir biçimde yanlış şekilde bağlanmıştı.
Murphy, “Yanlış yapmalarının herhangi bir yolu varsa, yapacaklardır” gibilerinden bir şeyler mırıldanarak suçu teknisyenlere attı. Ve aslında hikayenin onunla ilgili kısmı bitti. Olaydan kısa bir süre sonra bir basın toplantısı sırasında, muhabirlerden biri uçuş cerrahına MX981’in tehlikelerini sordu.
Stapp, ekibin Murphy kanunu adını verdiği şeyin farkında olması sayesinde projenin güvenliğinden emin olduğunu söyledi. Stapp, “Ters gidebilecek her şey ters gider” diyerek de bu kanunun ne olduğunu açıkladı. Bu sözler kısa süre içinde hafızalara yazılacaktı. Zaman içinde de Murphy kanunu popüler kültüre yerleşti.
Murphy Kanunu Gerçek mi?
Murphy kanunları elbette gerçekten bir “kanun” değildir. Bu terimi bilimde kullandığımız anlamda, yani gözlemlenen bir fenomen veya çok sayıda ampirik kanıtla desteklenen bir kavram biçiminde düşünmememiz gerekir. Bu nedenle daha ziyade bir özdeyiş biçiminde algılamamız gerekir.
Buna rağmen, başka bir bakış açısı ile ele alırsak Murphy kanunlarını bilimsel olarak da düşünebiliriz. Bu noktada aklımıza bir sistemin düzensizliğinin ölçüsü olan entropi gelmelidir. Termodinamiğin ikinci yasası “entropinin evrende ve onun içindeki varsayımsal olarak izole edilmiş herhangi bir sistemde her zaman artması gerektiğini” bizlere söyler.
Diğer bir deyişle, kendi hallerine bırakıldığında (yani, dış enerji girişi olmadan) bir ülke, bir ev, insan vücudu kısaca tüm sistemler bir galaksi, bir ülkenin ekonomisi, bir ev, hatta insan vücudu düzensiz hale gelme eğilimindedir. Elbette termodinamik gibi gerçek bir fizik konusu ile Murphy kanunları aynı şey değildir. Ancak bir şekilde ikisi de aynı temaya dokunur. Ne yaparsak yapalım bazen evren kendi kuralları ile hareket eder.
İnsanlar bilişsel önyargılarla doludur ve hepimiz olumlu deneyimlere kıyasla olumsuz deneyimleri daha fazla eğilim gösteririz. Bu nedenle tost ekmeğimizin reçel sürülü kısmı yere her düştüğünde aklımıza hemen Murphy yasaları gelir. Oysa ki önceki seferlerde bunun gerçekleşmediğini unuturuz.
Murphy Kanunu Ve Matematik
İngiliz matematikçi Philip Obadya; David Lewis ve Keylan Leyser ile birlikte bu kanunların olasılıklarını sayısal olarak hesaplayan bir formül de geliştirmişti. 1000’den fazla kişi üzerinde yapılan çalışmalar sonucunda ortaya çıkan formül aşağıdaki gibiydi.
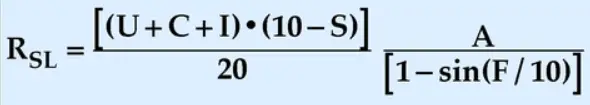
Murphy kanunlarının bu formül yardımı ile olasılıklarını hesaplamak isterseniz değişkenlere aşağıdaki gibi değerler vermelisiniz. Bunları yerine yerleştirdiğiniz zaman elde edeceğiniz sonuç 0 ve 8,6 değerleri arasında çıkar. Büyük değerler, kötü bir şeylerin olacağını gösterir.
- U, aciliyet. 1 ve 9 arası bir değer alır ve 9 en acil olan anlamına gelir.
- C, karmaşıklık. 1 ve 9 arası bir değer alır.
- S, görevi gerçekleştirme yeteneği. 1 ve 9 arası değer alır.
- A, görevin kötüye gidişidir ve sabit değerdir. 1000den fazla kişiyle yapılan anket sonucu değeri 0,7 olarak tespit edilmiştir.
- F, görevin yerine getirilme sıklığıdır. 1 ve 9 arası bir değer alır.
Sonuç Olarak;
Murphy’nin başlangıçtaki “Ters gidebilecek her şey ters gider” özdeyişini daha az kaderci biçimde de yorumlamak mümkündür. Aslında Dr. Stapp da bu sözü kaderci bir bakış açısıyla söylememişti.
Bir biçimde tedbirin öneminden ve bu sayede hayatının kurtulduğundan söz ediyordu. Sonucunda en düşük olası senaryolar bile bir biçimde gerçekleşme olasılığını taşır. Bu gerçek, sigorta komisyoncuları ve risk yönetimi uzmanları tarafından iyi bilinmektedir.
Murphy Yasası’nın zamanla daha geçerli hale gelmesi gerektiğini de akılda tutmakta fayda var. Sonucunda bir sistem ne kadar karmaşıksa bozulma olasılığı da o kadar fazladır. Günümüzde, internet gibi ağlar kullanarak sıklıkla birbirine bağımlı ve bağlı olan giderek daha karmaşık makinelerle çevriliyiz. Sonucunda 21. yüzyıl yaşamının karmaşıklığı, Murphy Yasası’nın bizi her zamankinden daha sık ziyaret etmesini sağlıyor
Kaynaklar ve ileri okumalar:
- Is Murphy’s Law actually true? Kaynak site: ZME Sceice. Yayınlanma tarihi: 30 Mayıs 2023. Bağlantı: Is Murphy’s Law actually true?
- How Murphy’s Law Works; Yayınlanma tarihi: 16 Nisan 2021; Kaynak site: How Stuff Works. Bağlantı: How Murphy’s Law Works/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel
