Zihnimizin nasıl işlediğini bilinçli olarak anlamak, onu geliştirmenin tek yoludur. Bu farkındalık, yaşamın her alanında daha net düşünmemizi ve daha sağlam kararlar almamızı sağlar. Eğer aklın bu evrensel ve etkileyici diliyle tanışmaya hazırsanız, rasyonelliğin dünyasına ilk adımı atmanın tam zamanı.

Akıl yürütmenin temellerini öğrenmek isteyen herkesin bilmesi gereken üç temel kural vardır. Bu “düşünme yasaları”, Antik Yunan’ın büyük filozofları Platon ve Aristoteles tarafından şekillendirilmiştir. Bugün kullandığımız tüm mantık sistemleri bu üç ilkeye dayanır.
İlki, özdeşlik yasasıdır. Bu yasa, bir şeyin kendisiyle aynı olduğunu söyler. Basit gibi görünse de, mantığın tüm yapısı bu temel ilkeye dayanır. Aristoteles’in ortaya koyduğu bu kural, düşüncenin kendi içinde tutarlı olmasını sağlar. Kısaca: bir şey neyse odur; başka bir şey değildir.
İkinci temel ilke, çelişmezlik yasasıdır. Bu yasa, bir önermenin aynı anda hem doğru hem yanlış olamayacağını söyler. Örneğin, “Tanrı vardır” ya da “Tanrı yoktur” denebilir; ama aynı anda hem “vardır” hem “yoktur” denemez. Bir düşünce ya doğrudur ya da değildir. İkisi bir arada olamaz.

Klasik mantığın en sağlam dayanaklarından biri olan bu yasa, özellikle modern felsefede tartışmaya açılmıştır. Hegel, Fichte ve Marx gibi düşünürler, karşıtlıkların çatışmasından doğan dönüşümü savunarak çelişkiyi düşüncenin dışlaması gereken bir hata değil, ilerlemenin kaynağı olarak görmüşlerdir. Bu yaklaşım, diyalektik düşüncenin temelini oluşturur.
Üçüncü temel ilke, üçüncü hâlin imkânsızlığı yasasıdır. Bu ilkeye göre, bir şey ya vardır ya da yoktur; bir önermenin aynı anda hem doğru hem yanlış olması mümkün değildir. Başka bir deyişle: her önerme ya doğrudur ya yanlıştır. Arada bir “belki”ye yer yoktur.

Bu yasa, bilginin mutlaklık yönünü vurgular. Mantık, belirsizliği reddeder; gri alanlara yer bırakmaz. Bu sayede düşünce, kararsızlıktan arınır ve tutarlılığa ulaşır. Akıl yürütme, bu netlik zemininde yükselir.
Önermeler mantığı nedir?
Bu mantık, düşüncenin en küçük birimi olan önermeleri inceler. Önermeler, doğru ya da yanlış olabilen ifadelerdir. Bu sistem, mantıklı düşünmenin temelini oluşturur. Bir argüman, genellikle birkaç öncül üzerine kurulur. Bu öncüller, sonucu destekleyen bilgi iddialarıdır. Ancak doğru bir sonuca ulaşmak için yalnızca doğru öncüller yeterli değildir; aynı zamanda geçerli bir düşünme biçimine de ihtiyaç vardır. İşte bu noktada çıkarım kuralları devreye girer.
1. Modus Ponens (Doğrulama Yolu)

Bu çıkarım biçiminde, koşullu bir önermeyi ve koşulun gerçekleştiğini biliriz. Bu durumda sonuç kaçınılmazdır. Bu, en temel ve sık kullanılan çıkarım kurallarından biridir. Yapısı şöyledir:
- (1) Eğer X doğruysa, Y de doğrudur.
- (2) X doğrudur.
- (3) O halde Y doğrudur.
Örnek:
(1) Eğer yağmur yağıyorsa, şemsiye almalıyız.
(2) Yağmur yağıyor.
(3) O halde şemsiye almalıyız.
2. Modus Tollens (Çürütme Yolu)
Bu düşünce biçimi, bir sonucun gerçekleşmediğini gözlemleyerek, o sonuca yol açması gereken durumu geçersiz sayar. Bu kural, doğru bir çıkarıma olumsuz yoldan ulaşmayı sağlar. Yapısı şöyledir:
- (1) Eğer X doğruysa, Y de doğrudur.
- (2) Y doğru değildir.
- (3) O halde X de doğru değildir.
Örnek:
(1) Eğer öğrenci ders çalışırsa, sınavı geçer.
(2) Öğrenci sınavı geçemedi.
(3) O halde öğrenci ders çalışmadı.
Modus Ponens ve Modus Tollens, mantıklı düşünmenin yapı taşlarıdır. Bu kurallar sayesinde bir argümanın geçerliliğini test edebilir, öncüller ile sonuç arasındaki bağlantının sağlam olup olmadığını görebiliriz. Düşüncenin tutarlılığını korumanın ve hatalı çıkarımları ayıklamanın en yalın ama en güçlü yollarıdır.
3. Ayrık Tasım (Disjunctive Syllogism)
Bu yapıda, iki olasılıktan biri dışlandığında geriye kalan tek seçenek, mantıksal olarak doğru kabul edilir. Bu çıkarım kuralı, şu yapıya dayanır:
- (1) Ya X ya da Y doğrudur.
- (2) X doğru değildir.
- (3) O halde Y doğrudur.
Örnek:
(1) Ya çok meşgulsün ya da benimle vakit geçirmek istemiyorsun.
(2) Çok meşgul değilsin.
(3) O halde benimle vakit geçirmek istemiyorsun.
4. Koşullu Tasım (Hypothetical Syllogism)
Bu çıkarım biçimi, koşullar arasında mantıksal bir zincir kurarak dolaylı ama geçerli bir sonuca ulaşır. Bu çıkarım biçimi, birbirine bağlı iki koşullu önermeyi zincirler:
- (1) Eğer X doğruysa, Y de doğrudur.
- (2) Eğer Y doğruysa, Z de doğrudur.
- (3) O halde: Eğer X doğruysa, Z de doğrudur.
Örnek
(1) Eğer insanlar özgür iradeye sahip değilse, eylemlerinden sorumlu tutulamazlar.
(2) Eğer eylemlerinden sorumlu değillerse, etik olmayan davranışları için cezalandırılmamalıdırlar.
(3) O halde: Eğer insanlar özgür iradeye sahip değilse, etik olmayan davranışları için cezalandırılmamalıdırlar.
Yüklem Mantığı Nedir?
Yüklem mantığı ya da birinci derece mantık, önerme mantığından daha ayrıntılı bir yapıya sahiptir. Önerme mantığı, önermeleri bölünemez bir bütün olarak ele alır; yüklem mantığı ise onların iç yapısını inceler. Bu mantık türü, anlamı analiz etmek için yüklemler ve niceleyiciler kullanır.
Bir yüklem, bir önermedeki öğeler arasındaki ilişkiyi tanımlar. Örneğin “Ayşe Elif’e güveniyor” önermesi yüklem mantığında G(x, y) biçiminde yazılır. Burada x, Ayşe’yi; y, Elif’i gösterir; G ise “güvenir” yüklemidir. Önerme, yalnızca Ayşe gerçekten Elif’e güveniyorsa doğrudur.
Niceleyiciler, bir özelliğin bir kümedeki hangi elemanlara uygulandığını belirtir. İki tür niceleyici vardır: tümel (∀) ve tikel (∃).
“Tüm kuşlar uçar” önermesinde niceleyici ∀, yani “her”dir; alan “kuşlar”, özellik “uçmak”tır. Bu durumda önerme ∀x (Kuş(x) → Uçar(x)) biçiminde yazılır. Buna karşılık, “Bazı kuşlar göç eder” önermesi tikel bir niceleme içerir ve ∃x (Kuş(x) ∧ Göç Eder(x)) biçiminde gösterilir.
Niceleme kurallarının en bilinenlerinden biri tümel açınımdır (universal instantiation). Bu kural, bir özellik bir kümenin tüm üyeleri için geçerliyse, o kümedeki herhangi bir eleman için de geçerli olacağını söyler. Örneğin: “Tüm kediler gece iyi görür” ve “Mira bir kedidir.” Buradan şu sonuç çıkar: “Mira gece iyi görür.”
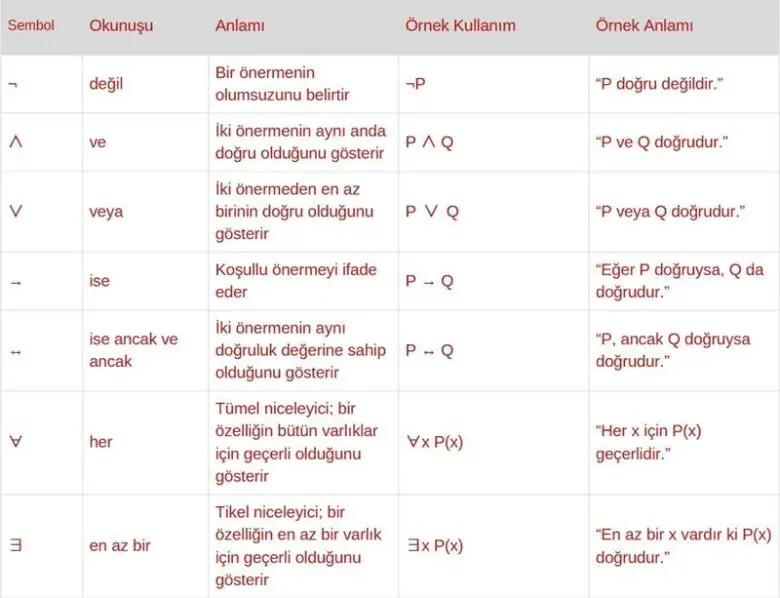
Yüklem mantığı bu tür sembolik gösterimlerle düşünceyi biçimsel bir dile dönüştürür. Kullanılan temel semboller şunlardır:
Geleneksel Mantık Neden Doğruluk Tablolarını Kullanmaz?
Günümüzde liselerde ve üniversitelerde öğretilen modern mantık doğruluk tablolarını kullanır; peki, geleneksel mantık neden bunlara yer vermez?
Çoğu insan mantıkla ilk kez lise yıllarında, matematik derslerinde tanışır. Bu derslerde karşılaştıkları doğruluk tabloları, filozof Ludwig Wittgenstein’ın geliştirdiği bir yöntemdir. Wittgenstein, karmaşık önermelerin doğruluk değerlerini sistemli biçimde çözümlemek için bu tabloları tasarlamıştır.
Günümüz mantığında doğruluk tabloları, bir önermenin bileşenleri arasındaki tüm olası doğru–yanlış kombinasyonlarını göstererek mantıksal tutarlılığı test etmenin pratik bir yolunu sunar. Buna karşılık, geleneksel mantık önermeleri biçimsel yapılarıyla değil, akıl yürütmenin anlamı ve kavramsal ilişkileriyle değerlendirir. Bu yüzden doğruluk tabloları klasik sistemin bir parçası değildir..
Kaynaklar ve ileri okumalar:
- Kamal, Maysara. “What Are the Rules of Logic? Your Guide to Mastering the Power of Reason” TheCollector.com, October 14, 2025, https://www.thecollector.com/what-are-the-rules-of-logic/
- Panovski, Antonio. “Philosophy 101: The 5 Major Branches of Philosophy Explained” TheCollector.com, September 5, 2023, https://www.thecollector.com/what-are-the-branches-of-philosophy/.
Matematiksel





