İnsanlar, bir sonraki otobüsü ne kadar bekleyeceklerinden tutun da önemli finansal kararlarına kadar pek çok konuda karşılarına çıkan problemleri çözmek için matematiği kullanır. Sayısal bilgi, modern yetişkin yaşamının merkezindedir çünkü sayılar her yerdedir. Ancak sayılarla arası kötü olan kişilerin, bu becerisi güçlü bireylere göre daha fazla zorluk yaşama olasılığı yüksektir. Bunun temel nedeni, matematiksel düşünme yeteneklerinin zayıf olmasıdır.

Sayılarla arası iyi olan kişiler, karar verirken sayısal bilgilere dikkat eder ve bu bilgiler üzerine düşünür. Sayıların ne anlama geldiğini bildikleri için kararlarını tutarlı biçimde verirler.
Buna karşılık, sayısal becerileri zayıf olan kişiler, somut verilerdense etkileyici hikâyelere ya da duygusal tepkilere yönelme eğilimindedir. Sayılar devreye girdiğinde, bu kişiler genellikle daha kötü kararlar verir. Buna iyi bir örnek Baltimore’daki bir borsacının hikâyesidir.
ABD’nin Baltimore kentinde yaşadığınızı varsayalım. Bir gün, tanımadığınız bir borsacıdan belirli bir hissenin hızla yükseleceğine dair bir haber bülteni alıyorsunuz. Bir hafta sonra, gerçekten de söz konusu hisse yükseliyor. Ertesi hafta yeni bir bülten geliyor. Bu sefer başka bir hissenin düşeceği öngörülüyor. Tahmin bir kez daha doğru çıkıyor.
Bu böylece on hafta boyunca devam ediyor. Her hafta gelen tahminler doğru çıkıyor. On birinci haftada ise bu gizemli kişiden özel bir davet alıyorsunuz. Sizi iş birliğine çağırıyor. Elbette bunun karşılığında yüksek bir komisyon talep edeceğini tahmin ediyorsunuz. Yine de bu size mantıklı ve cazip bir teklif gibi görünüyor. Ama gerçekten öyle mi?
Baltimorelu borsacı hikayesi ile ilgili sorun nerede?

Bu kişinin piyasalar hakkında hiçbir bilgisi olmayan bir dolandırıcı olma ihtimali yok gibi görünüyor. Sonuçta, üst üste on kez doğru tahminde bulunmak neredeyse imkânsız bir başarıdır. Yine de paranızı bu kişiye vermemelisiniz. Çünkü ilk bakışta fark edilmeyen önemli bir ayrıntı vardır.
İlk hafta, bu borsacının haber bülteni sadece size ulaşmadı. Toplam 10.240 kişiye gönderdi. Ancak bültenlerin içeriği aynı değildi. Yarısında, sizin aldığınız gibi, belirli bir hissenin yükseleceği yazıyordu. Diğer yarısında ise aynı hissenin düşeceği öngörülüyordu.
Tahmini yanlış çıkan 5.120 kişi bir daha borsacıdan haber almadı. Doğru tahmini almış olan siz ve sizinle aynı içeriği gören diğer 5.119 kişi ise ikinci hafta yeni bir bülten aldılar. Bu kez de ikiye bölünmüş yeni bir grup oluşturuldu. Yarısına bir hissenin yükseleceği, diğer yarısına düşeceği söylenecekti. Böylece ikinci kez doğru tahminle karşılaşan 2.560 kişi kaldı.
Bu süreç aynı şekilde devam etti. Onuncu haftanın sonunda, üst üste on kez doğru öngörü almış olan yalnızca on kişi kalacaktı. Borsacının amacı da bu son on kişiden yüksek komisyon alarak kazanç sağlamaktı.
Bu hikâyenin gerçek olup olmadığını bilmiyoruz. Ancak matematikçi Jordan Ellenberg, bu örneği How Not to Be Wrong: The Hidden Maths of Everyday Life adlı kitabında anlatıyor. Kendisinin de belirttiği gibi, bu hikâyeyi bir realite televizyon programında duymuş.
Matematiksel Düşünme Becerimizi Arttırmak İçin Ne Yapabiliriz?

Baltimorelu borsacı numarası işe yarar çünkü doğrudan yalan söylemez. Size yanlış bilgi vermez. Bunun yerine, sizi yanlış bir sonuca götürebilecek doğru şeyler söyler. Üst üste on hisse senedi tahmininin tutması ya da bir çift zarla art arda altı kez altı atılması gerçekten imkânsız gibi görünür.
Ama imkânsız görünen olaylar gerçekleşir. Üzerine yıldırım düşen ya da lotoyu kazanan insanlar da vardır. Bunlar da istatistiksel olarak çok düşük olasılıklı olaylardır. Bu nedenle, yaşananları doğru yorumlayabilmek için matematiksel düşünme becerilerine sahip olmak gerekir.
Peki ama matematiksel düşünme ile bir problem nasıl çözülür? Karşılaşılan problemlerde izlenecek özel bir yol var mıdır? Varsa nedir? Bu soruya “Evet” yanıtını 1940’lı yılların ortasında Macar bir matematikçi George Polya verdi.
Kendisi 1945’te onun herkes tarafından bilinirliğini arttıran ve günümüze kadar etkisini sürdüren How to Solve It (Nasıl Çözmeli?) isimli kitabını yazdı. George Polya, 17 dile çevrilen bu önemli eserinde bir matematikçinin problem çözümü için kat ettiği adımları “her seviyede kullanıcı” için özetlemiştir.
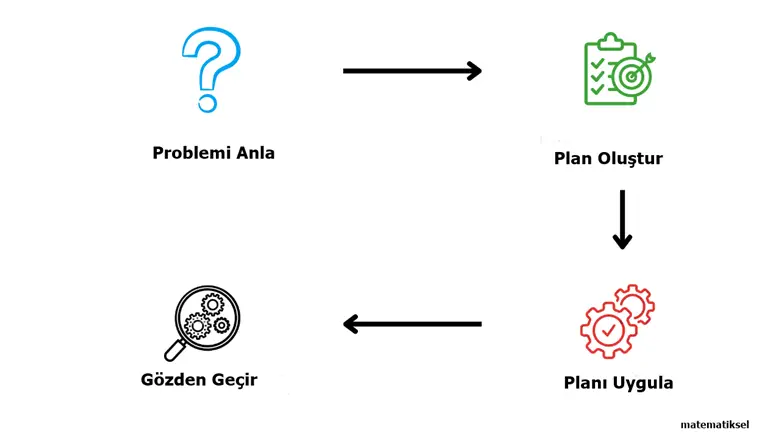
Pólya’nın problem çözme planı dört basit adımdan oluşuyordu. Sorunu anladığınızdan emin olun. Sorunu çözmek için bir plan yapın. Planı uygulayın ve sonucunu test edin.
Matematik Becerilerini Geliştirmek İçin Bazı Öneriler
Hayatınız nasıl ilerliyor olursa olsun, günlük yaşamda sayılarla karşılaşmamak neredeyse imkânsızdır. Sayılar, hem fiziksel sağlığınızı hem de finansal durumunuzu etkileyen kararların merkezindedir. Bu nedenle, sayılarla aranız ne olursa olsun, daha sayısal düşünmek için bazı temel adımlar atabilirsiniz.
İlk olarak, kendi becerilerinizi anlayın. Matematikte iyi olmadığınıza inanmak, doğru olmasa bile size zarar verir. Bu nedenle, matematik konusunda sandığınızdan daha yetenekli olabileceğinizi göz önünde bulundurun. Öte yandan, yeterince becerikli olmadığınız hâlde kendinize fazla güvenmek de yanıltıcı olur. Bu nedenle gerektiğinde yardım istemekten çekinmeyin.
İkinci olarak, insanlardan sayıları anlaşılır biçimde ifade etmelerini isteyin. Araştırmalar, sayıların nasıl sunulduğunun, neyin sunulduğu kadar önemli olabileceğini gösteriyor. Örneğin, bir haber bülteninde belirli bir yiyeceği yiyen her 100.000 kişiden 1’inin kansere yakalandığı yazsın. Bu ifade ilk bakışta korkutucu gelecektir. Ancak bu oranı yüzde cinsinden hesapladığınızda, sonuç yalnızca %0,001 olur.

Birçok insan için ilk sunum biçimi ciddi bir risk algısı yaratır. Oysa eşdeğer olan yüzde değeri çok daha küçük ve daha az tehditkâr görünür. Bu yüzden sayıları hem anlamak hem de doğru değerlendirmek için onların nasıl sunulduğuna dikkat etmek gerekir.
Ve son olarak: pratik, pratik, pratik. Basit işlemlerle başlayın. Toplama ve çıkarma gibi temel matematik becerilerini düzenli olarak çalışın. En önemlisi, geri bildirim alın. Ne yaptığınızı doğru ya da yanlış bilmeden öğrenme gerçekleşmez. Kendinize olan genel bakışınızı olumlu tutmak da sayısal becerilerinizi geliştirmenize yardımcı olur.
Sonuç Olarak
Kabul edelim muhtemelen okulda öğrendiğiniz tüm matematik bilgisini asla geri kazanamayacaksınız. Fakat küçük adımlar atarak etrafımızı saran sayılar ile olan ilişkimizi düzeltmemiz ve matematiksel düşünme becerimizi geliştirmemiz mümkün.
Kaynaklar ve ileri okumalar
- Math skills aren’t enough to get through hard decisions – you need confidence, too. Kaynak: Math skills aren’t enough to get through hard decisions – you need confidence, too
- How Not to Be Wrong: The Hidden Maths of Everyday Life by Jordan Ellenberg – review. Kaynak site: Guardian. Yayınlanma tarihi: 13 Haziran 2014. Bağlantı: How Not to Be Wrong. The Hidden Maths of Everyday Life by Jordan Ellenberg – review
- Jasper, John & Corser, Ryan & Corser, Ryan. (2017). Numeracy Predicts More Effortful and Elaborative Search Strategies in a Complex Risky Choice Context: A Process Tracing Approach. Journal of Behavioral Decision Making. 30. 224-235. 10.1002/bdm.1934.
- Keller C, Kreuzmair C, Leins-Hess R, Siegrist M. Numeric and graphic risk information processing of high and low numerates in the intuitive and deliberative decision modes. An eye-tracker study. Judgment and Decision Making. 2014;9(5):420-432. doi:10.1017/S1930297500006793
- Goodman, Jeffrey & Hanson, Carl & Auld, M. & Sherry, Cherylee & Strack, Robert & Mathis, Jerrica. (2013). Affordable Care Act: Opportunities and Challenges for Health Education Specialists Acknowledgements. 10.13140/2.1.2096.5447.
Matematiksel





