Manavların yüzyıllardır pratikte uyguladığı “piramit şeklinde istifleme” çözümünün matematiksel olarak doğrulanması, Kepler varsayımı adıyla bilinir ve bu varsayımın resmi kanıtı ancak 2017’de yayımlanmıştır.

Kepler Varsayımı Nedir?
Kepler varsayımı, adını 17. yüzyılda yaşamış matematikçi ve gökbilimci Johannes Kepler’den alır. Sorusu basittir ama yanıtı dört yüzyıldan fazla süredir bulunamamıştır: Eşit büyüklükteki küreleri, üç boyutlu Öklid uzayında en sıkı şekilde nasıl yerleştirebiliriz?
Günlük hayatta bu soru portakalları, topları ya da misketleri nasıl istifleyeceğimizle ilgilidir. Ama matematiksel olarak, bu düzenlemenin hangi geometrik biçimde en az boşluk bırakacağı sorusudur.

Kepler, en iyi yerleşimin portakal tezgâhlarında sıkça görülen piramit benzeri üçgen düzenleme olduğunu öne sürdü. Bu biçimde bir paketleme sonucunda yoğunluğun yaklaşık %74 olduğunu yazdı ama ispatını yapmadı. Bu iddia, bilgisayar destekli kanıtlarla ancak 1997’de doğrulanabildi.
Sorunu daha iyi anlamak için basit bir örneğe bakmak faydalıdır. Örneğin, aynı boyuttaki birkaç madeni parayı (yani daireyi) en az yer kaplayacak şekilde nasıl yerleştirebileceğimizi düşünebiliriz. Bu düzeni test etmek için paraların etrafına bir ip saralım ve ipin çevrelediği alanı hesaplayalım
Hangi Düzenleme Daha Verimli?
İki para için (n = 2) en ideal yerleşim kolayca bulunacaktır. Paraları temas edecek şekilde yan yana yerleştiririz. Bu durumda, iki parayı çevreleyen en kısa ip uzunluğu (4+2π)r olur. Toplam çevrelediği alan ise (4+π)r2 olur.
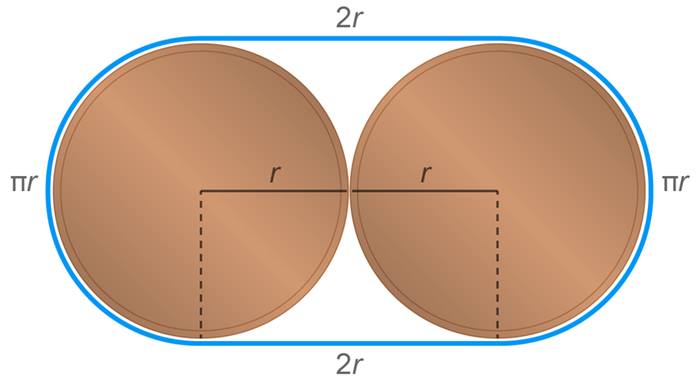
Üç para için (n = 3) iş karmaşıklaşır. Paraları sırayla düz bir hatta dizeriz veya paraları eşkenar üçgenin köşelerine yerleştiririz. Ama asıl soru şudur: Hangi yerleşim gerçekten daha verimli, yani daha az alan kaplar?
Görünüşe göre, üçgen biçiminde dizmek daha verimli. Matematiksel olarak incelendiğinde bu dizilimde ip uzunluğu: (6 + 2π)r ve kapladığı alan: (6 + √3 + π)r²olur. Buna karşılık yanyana dizdiğimiz zaman ip uzunluğu: (8 + 2π)r ve kapladığı alan (8 + π)r²olur.
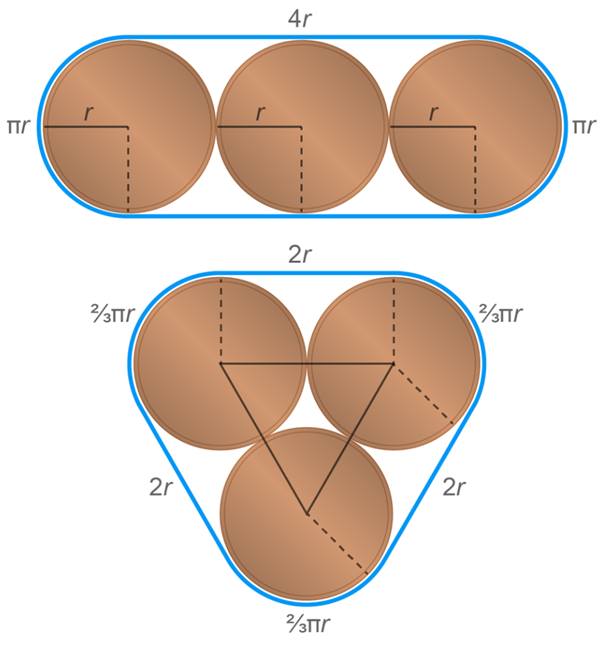
Aslında, gerekli ip uzunluğu ve kapalı alan için genel bir formül verilebilir. Paraları yanyana yerleştirme durumunda ip uzunluğu 4(n – 1 + 2π)r ve kapladığı alan 4(n – 1)r² + πr² olur. Oysa ki üçgen ızgara biçiminde dizersek ip uzunluğu 2(n + π)r ve kapladığı alan (2n + √3(n – 2) + π)r²olacaktır. Bu hesaplar, üçgen biçimli yerleşimin daha az yer kapladığını gösteriyor.
Ama bu gerçekten her zaman en iyi çözüm mü? Belki de daireleri tamamen düzensiz, kaotik bir biçimde yerleştirerek daha da az yer kaplamak mümkündür. İşte bu noktada Macar matematikçi László Fejes Tóth devreye giriyor. 1975’te öne sürdüğü varsayıma göre, n adet dairenin en verimli yerleşimi, üçgen bir ızgara üzerinde, mümkün olduğunca düzgün bir altıgen biçimi oluşturan düzendir.
2011 yılında matematikçi Dominik Kenn, bu fikrin n’in neredeyse tüm değerleri için geçerli olduğunu göstermeyi başardı. Aslında bu durum ilk kez 1773 yılında fizikçi ve matematikçi Joseph Louis Lagrange tarafından ele alındı. Lagrange, üçgen örgü düzeninin en verimli çözüm olduğunu buldu. Ancak, düzensiz yerleşimlerinin daha az yer kaplama ihtimali o dönemde dışlanmamıştı. Bu ihtimalin de elenmesi, 1940 yılında Fejes Tóth’un çalışmalarıyla mümkün oldu.
Küre Sayısı Arttıkça İşler Daha da Karışacaktır
Peki ya küreler? Kepler varsayımına göre, sonsuz sayıda özdeş küre, üç boyutlu bir hacmi en verimli biçimde doldurmak istendiğinde, üst üste dizilmelidir. İlk katmanda, küreler tıpkı iki boyutlu örnekteki madeni paralar gibi üçgen örgü şeklinde dizilir. İkinci katmanda ise, her boşluğa bir küre yerleştirilir. Üçüncü katman yine ilk katmanın aynısı olacak şekilde tekrarlanır ve bu düzen sonsuza dek devam eder.
Ancak konu sınırlı sayıda küre olduğunda işler oldukça değişir. Hangi düzenin daha az yer kapladığını görmek için bu farklı yerleşimlerde oluşan hacimleri karşılaştırmak gerekir.
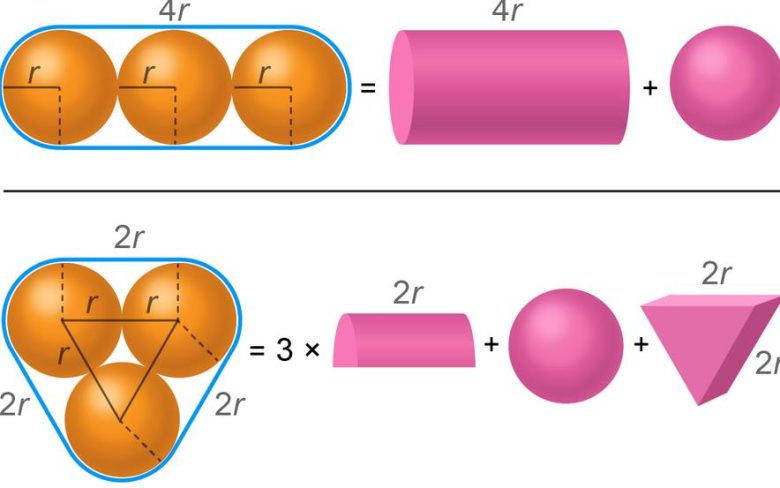
Küreleri yanyana koyarsak hesaplama kolaydır. Yapı, bir silindir ve bir küre olarak düşünülür. Bu durumda toplam hacim yaklaşık olarak (16⁄3)πr³ ≈ 16.76r³ olur. Üçgen dizilimin hacim hesabı daha karışıktır. Bu yerleşimde üç yarım silindir, bir üçgen prizma ve bir küre bulunur. Tüm parçaların hacmi toplandığında
(13⁄3)πr³ + 2√3r³ ≈ 17.08r³ eder. Bu durumda ilk hesaplama daha avantajlıdır. Aslında, dört küre için en verimli yerleşim yine bu dizilimdir.
Ancak küre sayısı arttıkça işler karmaşıklaşır. Matematikçiler, 55 küreye kadar yanyana dizmenin en verimli düzenleme olduğunu varsaymışlardı. Fakat 1992 yılında, Jörg Wills ve Pier Mario Gandini, 56 küre için küme yerleşiminin daha az hacim kapladığını ortaya koydu. Ancak bunun en iyi düzenleme olup olmadığını kanıtlayamadılar. Aslında zaman içinde sonuçlar daha da şaşırtıcı bir hal aldı. Günümüzde biliyoruz ki:
- 1–55 arası kürelerde: Yanyana yerleşim büyük olasılıkla en iyisi.
- 56 kürede: Küme yerleşimi daha verimli.
- 57–58 kürede: Yanyana düzeni tekrar öne geçiyor.
- 59–62 kürede: Küme tekrar en verimli hale geliyor.
Bu sonuçlar ilk bakışta sezgisel gelmeyebilir. Ve şu ana kadar hiç kimse, bu geçişlerin neden bu şekilde olduğunu tam anlamıyla kanıtlayabilmiş değil.
Sonuç Olarak
Matematikçiler üç boyutta duracak insanlar değildir. Peki dört boyutlu uzayda, dört boyutlu topların en verimli yerleşimi nasıl olur? Gandini ve çalışma arkadaşı Andreana Zucco, 1992’de yayımladıkları çalışmada şunu gösterdi: d = 4 için, eğer en az n = 375.769 top varsa, küme dizilimi daha az yer kaplar.
Beş ya da daha yüksek boyutlarda, sonlu sayıda top için en iyi yerleşim her zaman yanyanadır. Bu varsayım henüz kesin olarak kanıtlanmamış olsa da, Betke ve Martin Henk 1998’de bunun 42 veya daha yüksek boyutlar için geçerli olduğunu da göstermişti. Muhtemelen bu kadarını Kepler bile hayal edemezdi.
Kaynaklar ve İleri Okumalar:
- Mathematical mysteries: Kepler’s conjecture; yayınlanma tarihi: 1 Eylül 2017; Bağlantı: https://plus.maths.org
- Gift Wrapping Five Oranges Has Outwitted the Best Minds in Mathematics for Generations. Yayınlanma tarihi: 6 Haziran 2023. Kaynak site: Scientific American. Bağlantı: Gift Wrapping Five Oranges Has Outwitted the Best Minds in Mathematics for Generations
- Sloane, N.. (1998). Kepler’s Conjecture Confirmed. Nature. 395. 435-436. 10.1038/26609.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





