Bir labirentten çıkmak bugün bize sıradan bir oyun gibi görünse de, bilgisayar bilimcileri ve matematikçiler bu yapıların ardındaki derin karmaşıklığa hâlâ büyük bir hayranlık duyar.

Antikçağda labirentler birer bulmaca olarak görülmezdi. En eski örneklerden biri, Girit Adası’nda inşa edilen ünlü hapishaneydi. Efsaneye göre bu yapı, Atinalı ustası Daidalos tarafından Kral Minos için yapılmıştı.
Minos, oğlu Androgeus’un kimliği bilinmeyen Atinalılar tarafından öldürülmesini unutmuyordu. Buna ek olarak, karısı Pasiphae’nin bir boğaya âşık olması ve insan–boğa karışımı Minotauros’u doğurması onu utandırmıştı. Minos hem bu utancı gizlemek hem de Atinalılardan intikam almak için her yıl yedi genç Atinalıyı bu labirente kapattı. Labirentin merkezinde ise insan yiyen Minotauros bekliyordu.

Atina Kralı Aigeus’un oğlu Theseus, kurban olarak gönderilen gençler arasına katılmak için gönüllü oldu. İronik biçimde Minos’un kurnaz kızı Ariadne bir Atinalıya, yani Theseus’a âşık olmuştu. Bu yüzden ona Minotauros’u öldürmesi için bir kılıç, dışarı çıkabilmesi için de yolunu işaretleyecek bir ip verdi. Theseus canavarı öldürdü ve ipi takip ederek dışarı çıktı; böylece Ariadne ile yeniden buluştu.
Aigeus, görevi başarıyla tamamladığında Theseus’un gemisine beyaz yelken çekmesini istemişti. Ama Theseus bunu unuttu. Efsaneye göre Aigeus uzaktan siyah yelkenleri görünce oğlunun öldüğünü sandı ve kendini denize attı. O denize daha sonra onun adı verildi: Ege Denizi.

Girit Labirenti, yüzyıllar boyunca hükümdarları, filozofları, matematikçileri, sanatçıları ve yazarları büyülemiştir. Pek çok antik yapı ve şehir, labirenti andıran düzenlerle inşa edilmiştir. Mısır piramitleri ile Akdeniz dünyasındaki yer altı mezar ağları olan Hristiyan katakombları buna örnektir. Bu tür yapılardaki amaç muhtemelen, ölümden sonra doğru yolu bulma yetisini sınamaktı.
Rönesans Avrupa’sında ise labirent figürleri duvar resimlerine ve zemin süslemelerine işlenmiştir. Ayrıca birçok bahçe, kesilmiş çitlerle çevrili gerçek labirentler şeklinde tasarlanmıştır.

Bir Labirentten Çıkmak İçin Bir Kaç Metot Mevcuttur
Bir labirentten çıkmak için öncelikle ne tür bir labirentte olduğunuzu bilmeniz gerekir. Çoğu çözüm yöntemi yalnızca “basit” labirentlerde işe yarar; yani köprü, kestirme yol veya başladığınız noktaya geri döndüren döngüsel geçitlerin bulunmadığı türlerde.
Eğer labirent basitse, en bilinen yöntem “duvar takibi”dir. Bir elinizi duvara koyar ve temasınızı hiç kesmeden ilerlersiniz. Bu yöntemle sonunda çıkışı bulmanız mümkündür.
Çünkü labirentin duvarlarını hayali olarak kaldırıp yapıyı açarak düz bir çizgiye dönüştürdüğümüzde, kapalı bir çevre elde ederiz. Bu çevre sizi kaçınılmaz olarak dış sınıra ulaştırır. Ancak başlangıç veya çıkış noktası labirentin tam merkezindeyse, bu yöntem her zaman işe yaramaz.
Eğer labirentin içinde birbirine bağlı olmayan döngüler varsa, sonsuz bir döngüye kapılmanız mümkündür. Ayrıca, giriş ya da çıkış noktası dış sınırla bağlantılı değilse de bu yöntem başarılı olmayacaktır.
Bu tür durumlar özellikle karmaşık labirentlerde oldukça yaygındır. Bu nedenle, farklı labirentten kurtulma algoritmaları geliştirilmiştir. Bu yöntemlerden biri de Trémaux Algoritması’dır ve karmaşık yapılı labirentlerde bile her durumda işe yarayan etkili bir çözümdür.
Trémaux’un Algoritması Nasıl Çalışır?
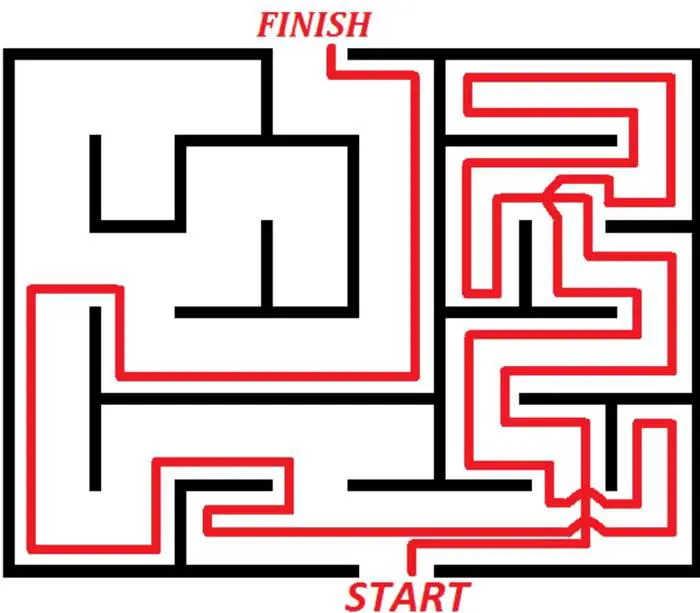
Hansel ile Gretel gibi, yürürken arkanızda “ekmek kırıntıları” bıraktığınızı hayal edin. Ardından şu kuralları aklınızda tutun:
Yeni bir kavşağa ulaştığınızda — yani ileride hiç kırıntı yoksa — rastgele bir yön seçin. Bu yol sizi başka bir kavşağa götürdüğünde, eğer seçeneklerden biri tanıdıksa, diğeri ise hiç denenmemişse, her zaman keşfedilmemiş olanı tercih edin. Eğer bir yol bir kez, diğeri iki kez kullanılmışsa, bir kez kullanılanı seçin ve geçerken ikinci izinizi bırakın.
En temel kural şudur: Üzerinde iki iz bulunan bir yola asla geri dönmeyin. Bu yöntemi kararlılıkla uygularsanız, labirent ne kadar karmaşık olursa olsun sonunda çıkışı bulursunuz.
Pledge Algoritması
Pledge Algoritması, özellikle döngüler ve sapmalar içeren karmaşık labirentlerde işe yarayan bir yöntemdir. Mantığı, sabit bir yön belirlemek ve kaç kez dönüldüğünü dikkatle takip etmektir.
nce bir yön seçersiniz; örneğin doğu. Engel görmediğiniz sürece hep bu yöne yürürsünüz. Bir duvar karşınıza çıkınca ona yaslanır ve duvar boyunca ilerlemeye başlarsınız. Bu sırada her dönüşünüzü sayarsınız. Sağ dönüşleri artı, sol dönüşleri eksi olarak düşünürsünüz.
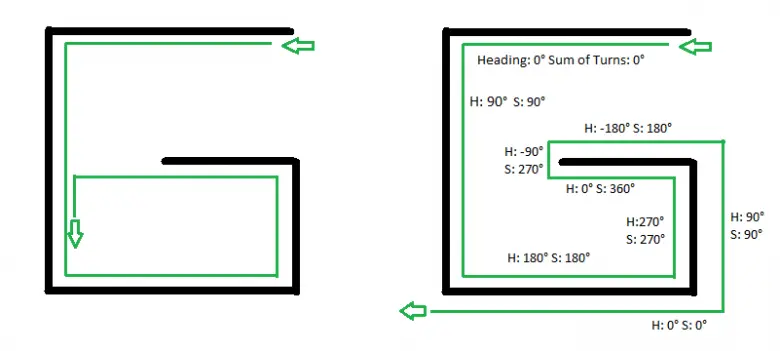
Duvar sizi döndürüp dolaştırsa da, toplam dönüşünüz yeniden sıfıra gelene kadar duvardan ayrılmazsınız. Toplam dönüş sıfır olduğunda ve yüzünüz tekrar ana yöne baktığında duvarı bırakır, hedef yönünüze doğru yürümeye devam edersiniz. Bu yöntem, ne kadar karmaşık olursa olsun, labirentin içinde kaybolmadan çıkabilmenizi sağlar.
Günümüzde çoğumuz günlük yaşamda bir labirentten çıkmaya çalışmıyoruz. Ancak bir bilgisayar programcısı için bu tür algoritmalarla uğraşmak hâlâ sıradan bir iştir.
Kaynaklar ve ileri okumalar
- How to escape a maze – according to maths. Yayınlanma tarihi: 26 Ocak 2017; Kaynak site: Conversation. Bağlantı: https://doi.org/10.64628/AB.34mwvjpnp
- The story of the Minotaur; Yayınlanma tarihi: 1 Mart 2001; Kaynak site: Plus Math. Bağlantı: The story of the Minotaur;
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





