Galileo Galilei, “Evrenin kitabı matematik diliyle yazılmıştır” demişti. Bu çarpıcı ifade, yalnızca bilim tarihine yön vermekle kalmaz, aynı zamanda bugüne kadar süregelen temel bir tartışmanın da kapısını aralar: Matematik gerçekten bir dil midir? Eğer öyleyse, bu dilin yapısı, kuralları ve işleyişi nasıldır?

Matematiğin sözcükleri ve sembolleri, düşünmeyi tetiklemek, merak uyandırmak ya da bazen yalnızca gülümsetmek için vardır. Kimi zaman toplumsal hayal gücünü ateşler, kimi zaman da anlamayı zorlaştırır. Bu kelimeler ve semboller, matematiği bugün ulaştığı zengin ve güçlü konuma taşıdı. Yine de temel bir soru hâlâ geçerliliğini koruyor.
19. yüzyılın ikinci yarısında Yale Üniversitesi’nde matematiksel fizik profesörü olan Josiah Willard Gibbs, istatistiksel mekaniğin öncülerindendi. Kendisi genellikle sessizliğiyle tanınırdı.. Ancak bir fakülte toplantısında matematiğin yerini yabancı dillerin alması gündeme gelince ayağa kalktı ve net bir çıkış yaptı: “Beyefendiler, matematik bir dildir.”
Gibbs, matematiği bir dil olarak tanımlayan ilk bilim insanı değildi. Ondan 200 yıl önce, İtalyan astronom Galileo Galilei aynı şeyi düşünüyordu. Il Saggiatore (Denemeci) adlı eserinde şöyle yazdı: “Evren, biz onun yazıldığı dili öğrenip harflerine aşina olmadıkça okunamaz. Bu dil, matematik dilidir.”

Galileo, bilim insanlarının o dönemde tercih ettiği Latince yerine İtalyanca yazmayı seçti. Amacı, bilimsel olmasa da okuryazar olan geniş bir kitleye ulaşmaktı. Ancak, tıpkı Platon’un Akademisi’nde kapıya asıldığı söylenen “Geometri bilmeyen giremez” uyarısı gibi, Galileo da okurlarını kitabın belli bir “dil bilgisi” gerektirdiği konusunda önceden uyarıyordu. Onun için matematiğin harfleri; üçgenler, daireler ve diğer geometrik şekillerdi.
Matematik Bir Dil midir?
Eğer matematik bir dilse, başka bir dile bağlı olmadan anlaşılması gerekir. Bu düşünce, evrensel olarak okunabilen müzik notaları düşünüldüğünde hiç de uzak görünmez. Peki bu mümkün mü? Basit bir örnekle deneyelim.
İlk birkaç doğal sayıyı toplayalım: 1, 2, 3, 4, 5. Kolay: Toplamları 15. Peki ya ilk 100 sayının toplamı? Görselde 1 + 2 + 3 + 4 + 5 toplamı, siyah ve kırmızı noktalarla iki kez gösteriliyor. Bu düzenlemede toplam noktaları saymak kolay: 5 × 6 = 30. Fakat her sayı iki kez sayıldığı için sonucu ikiye bölmek gerekiyor: 30 ÷ 2 = 15.

Bu yöntemin güzelliği, fikri bir bakışta kavratabilmesidir. Ayrıca burada 5 sayısının bir ayrıcalığı yok. 100 sayıya da aynı şekilde bakabiliriz. O hâlde 1 + 2 + … + 100 toplamı da 100 × 101 ÷ 2’dir. Sonuç: 5.050. Aynı yöntemle, ilk N doğal sayının toplamını da bulabiliriz: N × (N + 1) ÷ 2
Tüm görsel anlatımlara rağmen, matematiksel düşüncenin tamamen kelimelerden bağımsız olması pek olası değil. Görselleri yorumlarken zihnimiz otomatik olarak kelimeler üretir; kelimelerse imgeler çağrıştırır. Bu karşılıklı ilişki, sonunda sözcüklere döneriz.
1940’larda Jacques Hadamard, dünyanın dört bir yanındaki matematikçilere şöyle sordu: “Düşünürken kelimeler mi kullanıyorsunuz, yoksa imgeler mi?” Cevap vereneler arasında Albert Einstein da vardı. Einstein yanıtında, düşüncelerinin yazılı ya da sözlü dile değil, yeniden üretebildiği işaretler ve görüntülere dayandığını söyledi.
Ancak yalnızca imgelerle düşünmenin sınırları vardır. 1983’te Vaughan Jones, karmaşık cebirsel bir yapıyı göstermek için yalnızca büyük siyah bir nokta kullandı. Bu görsel, hem teorik bir yaklaşıma hem de görsel anlatımın sınırlarına yapılan bir espriydi.
Bir İsim Ne Anlatır?
“Bir ismin mutlaka bir anlamı mı olmalı?” diye sordu Alice kuşkuyla. Humpty Dumpty ise kesin bir yanıt verdi: “Elbette olmalı.” Lewis Carroll’un Aynanın İçinden adlı kitabındaki bu diyalog, matematikte kullanılan terimler için de geçerlidir.
Maryland Üniversitesi’nden matematikçi James Yorke da Alice’e aynı cevabı verirdi. Kendisi ile yapılan bir sohbette, “kaos” kelimesini nasıl benimsediğini anlattı. Yorke, kelimelerin anlam taşıması gerektiğini düşünüyordu. İnsanların hayatlarındaki rastlantısallığa dair hislerini yakalamak istiyordu.
Matematikteki çoğu terimi sadece uzmanlar bilir. Kaos bunun istisnası oldu. On yıl içinde, James Gleick’in Kaos: Yeni Bir Bilimin Doğuşu adlı kitabı çok satanlar listesine girdi. Bu kitap, meteorolog ve matematikçi Edward Lorenz’in çalışmalarıyla başlıyordu.
Lorenz, 1961’de hava modelleri üzerinde çalışırken, başlangıç koşullarındaki küçük değişimlerin zamanla büyük farklara yol açtığını fark etti. Bu, matematikçiler için yeni olmasa da—Fransız matematikçi Henri Poincaré bunu 20. yüzyılın başında yazmıştı—pek çok bilim insanı için sarsıcıydı.
Lorenz’in meşhur örneği şuydu: “Bugünkü bir fırtınaya, haftalar önce Brezilya’da kanat çırpan bir kelebek neden olmuş olabilir.” Bu fikir, daha sonra kelebek etkisi olarak anılacaktı. Bir matematik teriminin geniş kitlelerde ilgi uyandırması için hayal gücünü ateşlemesi gerekir. Güçlü bir imge bunu kolaylaştırır. Kaos örneğinde, bu imgeyi bizzat Edward Lorenz sağlamıştı.
Matematik Dilini Doğru Kullanmak Önemlidir
Kimi zaman kötü seçilmiş kelimeler, matematiğin gelişimini sekteye uğratır. René Descartes bunun erken bir örneğidir.
Cebirsel denklemleri incelerken, Descartes bazı sayıların kendileriyle çarpıldığında negatif sonuç verebileceği fikrini ele aldı. Ancak sayı doğrusunda böyle bir sayı yoktu. Descartes bu tür sayılara imaginaire (hayali) adını verdi.
Hayali sayı ifadesi zamanla yayılsa da Carl Friedrich Gauss, bu terimden hoşlanmıyordu. 1831’de şöyle yazdı: “Bu konu gizem ve karanlıkla çevriliyse, bunun en büyük sebebi uygun olmayan terminolojidir.” Gauss, daha kapsayıcı olan karmaşık sayılar terimini tercih etti. Ne yazık ki, Descartes’ın ifadesi hâlâ kullanılmakta.
1670 yılında Isaac Newton, hareket eden sıvının konumunu ve hızını tanımlamak için fluents, fluxions ve hatta ffluxions gibi terimler türetti. Ancak bu kelimeleri kesin biçimde tanımlamak Newton için bile zordu. Yüz yıldan uzun süre boyunca matematikçiler bu terimleri açıklamaya çalıştı ama başarılı olamadılar. 1800’lerde, limit ve türev gibi sağlam tanımlar geliştikçe, Newton’un bu “f’li kelimeleri” terk edildi.
1801’de Cambridge profesörü John Colson’un bir kitabı yayımlandı. Bu kitap, Maria Agnesi’nin 1748 tarihli kalkülüs kitabının İngilizce çevirisiydi. Ancak Colson yeterince İtalyanca bilmiyordu. Sadece çeviri yapacak kadar öğrenmişti ve bu sırada ciddi bir hata yaptı.
Agnesi kitabında bir eğriyi tanımlarken şöyle yazıyordu: “la curva… dicesi la Versiera.” Versoria, yelken yönünü değiştirmeye yarayan halat anlamına gelir. Görsel bir çağrışım içeriyordu. Ancak Colson bu kelimeyi hiçbir sözlükte bulamadı. En yakın benzeri olan l’avversiera kelimesine yöneldi—bu da “cadı” anlamına geliyordu.
Bugünün kalkülüs kitaplarında bu ifade hâlâ Agnesi’nin Cadısı olarak geçer ve öğrenciler bu eğriye bakarak hâlâ “bunu hangi uğursuz güç çizdi acaba?” diye düşünmeden edemez. Oysa Maria Agnesi, hayatını dindarlığa ve yoksullara yardıma adayan bir kadındı.
Matematik Sembollerinin Kökeni Kelimelerdir
Matematikte sembolleri, aslında kelimelerden evrilmiştir. Bunun bir örneği, bugün çıkarmada kullandığımız eksi işaretidir. Orta Çağ Avrupa’sında çıkarma işlemi kelimelerle yazılırdı: minus (Latince), moins (Fransızca), meno (İtalyanca).
15. yüzyıla gelindiğinde bu kelimeler kısaltılarak m– biçiminde yazılmaya başlandı. Ardından, 1489 yılında Johannes Widmann’ın ticari hesaplara dair yayımladığı bir kitapta şu ifadeye yer verdi. “–, daha azı; +, daha fazlası ifade eder.”
Semboller, kelimelerin yerine geçmekten fazlasını yaparlar. Calculus’un keşfini Newton’la paylaşan Gottfried Wilhelm Leibniz de bu düşüncedeydi. Sembollere öylesine hayrandı ki, yalnızca sembollerden oluşan evrensel bir dil hayal etti. Ona göre bu dil, “fikirlerin alfabesi” olmalıydı.
Leibniz bu hayaline ulaşamadı. Ancak başkaları başarılı oldu. Alman matematikçi ve filozof Gottlob Frege, 1879’da yayımladığı 88 sayfalık Begriffsschrift adlı kitapta, biçimsel mantığın niceleyicileri ilk kez yer aldı. Frege bu çalışmasını şöyle tanımlıyordu: “Aritmetiğe dayalı, saf düşüncenin formül dili.”

Kitapta yer alan diyagramlar yalnızca yatay değil, dikey olarak da sayfaları kaplıyordu. Bugün birçok uzman, Begriffsschrift’i mantık tarihindeki en önemli tek eser olarak görür. Ancak kendi zamanında bu eser alayla karşılanacaktı.
Günümüzden bir örnek ise 2016’da ortaya çıkan quon dilidir. Harvard Üniversitesi’nden Zhengwei Liu, Alex Wozniakowski ve Arthur M. Jaffe tarafından geliştirilen bu sistem, parçacık benzeri uyarımların ve onlara etki eden dönüşümlerin üç boyutlu görsel temsillerine dayanır.
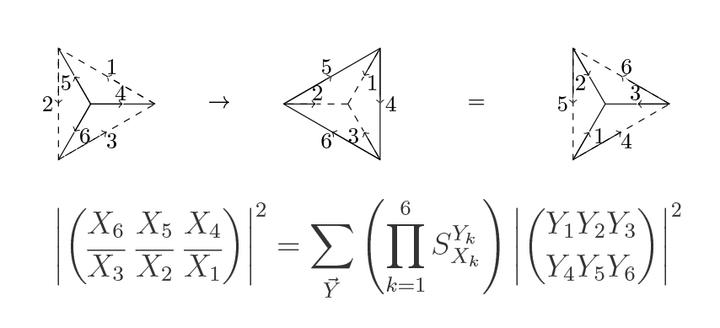
Quon dilinin amacı yalnızca kuantum bilgi kuramını açıklamak değildir. Aynı zamanda cebir ve topoloji alanlarında ispatlar üretmeye de olanak tanır. Harvard Gazette’e verdiği röportajda Jaffe şöyle der: “Bu görsel matematik dili, klasik cebirsel yöntemlerde olmayan düşünme yolları sunuyor.” Ve ekler: “Bazen bir görsel, bin sembole bedeldir.”
Kaynaklar ve İleri Okumalar:
- Silver, Daniel. (2017). The New Language of Mathematics. American Scientist. 105. 364. 10.1511/2017.105.6.364.
- Waller, Patrice & Flood, Chena. (2016). Mathematics as a universal language: transcending cultural lines. Journal for Multicultural Education. 10. 294-306. 10.1108/JME-01-2016-0004.
Matematiksel