Markov zinciri, bugün birçok algoritmanın arka planında fark edilmeden işler. Kimyasal süreçleri, ekonomik eğilimleri ve nüfus hareketlerini modellemede merkezi rol oynar. Aynı yaklaşım, internetin yapısında gezinmeyi mümkün kılan matematiksel zemini de kurar. İlginç olan, Rus matematikçi Andrey Markov’un bu kuramı geliştirirken onu bilimsel istatistikler üzerinde değil, Puşkin’in şiirleri üzerinde denemeyi tercih etmiş olmasıdır.

Bir kitabın ilk 20.000 harfini inceleyip frekansları saydığınızı ve örüntüleri araştırdığınızı düşünün. Andrey Markov’un, Aleksandr Puşkin’in manzum romanı Eugene Onegin’i analiz ederken yaptığı tam olarak buydu.
Markov, metinde ünlü ve ünsüzlerin nasıl ardışık geldiğini inceledi. Bir ünlünün ardından başka bir ünlünün ya da bir ünsüzün gelme olasılıklarını bu yolla çıkardı. Bunu yaparken, 1906 yılında geliştirdiği ve bugün Markov süreci ya da Markov zinciri olarak adlandırdığımız istatistiksel modeli uyguluyordu. Markov’un keşfi, başka bir Rus matematikçi olan Pavel Nekrasov ile yaşadığı bir tartışmadan doğdu.

Markov zinciri nedir?
Olasılık kuramının temel taşlarından biri büyük sayılar yasasıdır. Bu yasa, bir paranın her atılışının önceki atılışlardan tamamen bağımsız olduğu durumda, atış sayısı arttıkça yazı ve tura sayılarının giderek yüzde elli–elli oranına yaklaşacağını söyler. Dört atışta tüm sonuçların yazı gelme olasılığı on altıda birdir. Ancak atış sayısı arttıkça, bu yüzde elli–elli dengeden sapma olasılığı azalır.
Nekrasov bunun tersinin de doğru olması gerektiğine inanıyordu. Ona göre, bir dizi eylemin ürettiği veriler büyük sayılar yasasına uyuyorsa, her bir eylemin sonucunun da önceki sonuçlardan bağımsız olması gerekirdi. Bu düşünceyi şaşırtıcı bir iddiaya dayanak yaptı. Rusya’daki suç istatistikleri büyük sayılar yasasına uyduğuna göre, suç işleyenlerin kararları da birbirinden bağımsız özgür irade eylemleri olmalıydı.

Markov bu hatalı mantık karşısında dehşete düştü. Nekrasov’un iddiasını “matematiğin kötüye kullanımı” olarak niteledi ve bunu çürütmeye kararlıydı. Bunun için, her bir sonucun olasılığının önce olanlardan etkilendiği, buna rağmen uzun vadeli davranışın yine de büyük sayılar yasasına uyduğu bir veri kümesine ihtiyaç duyuyordu.
Bir paranın yazı mı tura mı geleceği önceki atışlara bağlı değildir. Bu yüzden Markov’un aradığı model bu değildi. Ancak sınırlı bir bağımlılık eklenirse durum değişir. Buna göre bir sonraki olay, yalnızca hemen önce gerçekleşen olaya bağlı olur; sistemin bu duruma hangi yoldan geldiği önemini yitirir. Olasılığı sadece bir önceki duruma bağlı olan bu tür olay dizilerine Markov zinciri denir
Markov zinciri ile nasıl hesaplama yaparız?
Hava durumu tahmini buna iyi bir örnektir. Yarının havası kuşkusuz bugünkü duruma bağlıdır. Ancak geçen hafta yaşananların doğrudan bir etkisi yoktur.
Şu basit modeli ele alalım. Hava yalnızca üç hâl alabilir: güneşli, bulutlu ya da yağmurlu. Bugün hava güneşliyse, yarın güneşli olma olasılığı yüzde 60’tır. Bulutlu olma olasılığı yüzde 30, yağmurlu olma olasılığı ise yüzde 10’dur. Bugün hava bulutluysa tablo değişir. Yarın yağmur ihtimali yüzde 50’ye çıkar. Havanın bulutlu kalma olasılığı yüzde 30, güneşli olma olasılığı ise yüzde 20’dir.
Bu modelde yarının havası yalnızca bugünkü havaya bağlıdır. Örneğin iki haftadır kesintisiz güneşli günler yaşanmış olması sonucu etkilemez. Bugün hava yağmurluysa, model yarın için yine yüzde 50 yağmur olasılığı öngörür. Bu geçiş olasılıklarını, düzenli bir biçimde göstermek için bir matris içinde ifade ederiz.
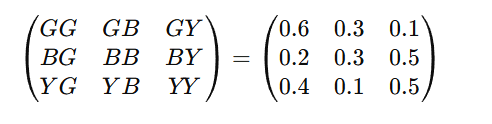
Bu modelle, güneşli bir günden başlayarak iki gün sonra yağmur olma olasılığını hesaplayabiliriz. Elbette bu sonuca ulaşmanın birden fazla yolu vardır. Bu nedenle tüm olası geçişlerin olasılıklarını toplamak gerekir. İki gün sonra yağmura ulaşan yollar şunlardır. GGY (Güneşli–Güneşli–Yağmurlu), GBY (Güneşli–Bulutlu–Yağmurlu) ve GYY (Güneşli–Yağmurlu–Yağmurlu).
- GGY yolunun olasılığı, GG olasılığı ile GY olasılığının çarpımıdır: 0.6 × 0.1 = 0.06
- GBY yolunun olasılığı, GB olasılığı ile BY olasılığının çarpımıdır: 0.3 × 0.5 = 0.15
- GYY yolunun olasılığı ise GY olasılığı ile YY olasılığının çarpımıdır: 0.1 × 0.5 = 0.05
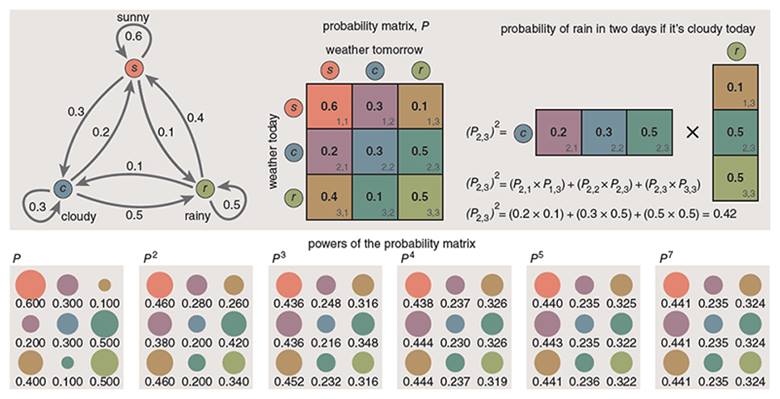
Bu da şu anlama gelir: güneşli bir günden iki gün sonra yağmur olma olasılığı, yani G×G durumu, bu üç yolun olasılıklarının toplamıdır. 0.06 + 0.15 + 0.05 = 0.26
Markov zinciri ne işe yarar?
Bu yöntem, ikinci gün yağmur olasılığını hesaplamak için de kullanışlı bir araç sunar. Bu araç, olasılık matrisimizin iki kopyasını birbiriyle çarpmaya dayanır.
Çarpım sonucunda ortaya çıkan matrisin her bir girdisi, iki adımda bir durumdan başka bir duruma geçme olasılığını temsil eder. Örneğin G×Y, bugün hava güneşliyken iki gün sonra yağmurlu olma olasılığını verir. Matrisin karesi, tüm olası iki günlük senaryoları aynı anda kapsar.
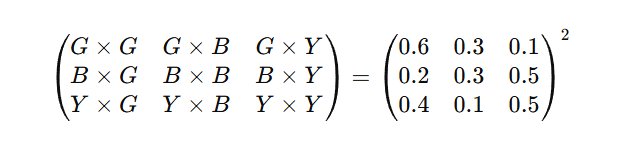
Hava durumu günden güne bir önceki güne bağlıdır. Ancak bu bağımlılık uzun vadede etkisini kaybeder. Olasılık matrisini art arda çarptığımızda, her satırdaki değerler giderek birbirine yaklaşır. Sonuçta uzun vadeli tahmin, bugünkü hava durumundan bağımsız hâle gelir. Buna karşılık kısa vadede, yani yarınki hava, bugünkü duruma bağlı kalır.
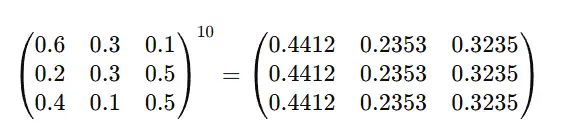
Bu matrisin her satırı, on gün sonraki bir günün güneşli, bulutlu ya da yağmurlu olma olasılığını temsil eder. Artık bugünkü havanın ne olduğu, yani hangi satırı seçtiğimiz, sonucu etkilemez. Onuncu gündeki olasılıklar her durumda aynıdır.
Markov, bu yolla Nekrasov’un uzun vadeli suç istatistiklerinin özgür iradenin varlığını gösterdiği yönündeki inancının hatalı olduğunu kesin biçimde ortaya koyan bir kanıt geliştirmişti.
Markov bu fikri somutlaştırmak için Puşkin’in şiirini kullandı. Şiiri yalnızca bir veri kümesi olarak ele aldı. Metnin yaklaşık sekizde birine karşılık gelen ilk yirmi bin harfi inceledi. Kaçının ünlü, kaçının ünsüz olduğunu saydı. Sonuçta harflerin yüzde 43’ünün ünlü, yüzde 57’sinin ünsüz olduğunu buldu.
Bu durumda rastgele bir harf seçildiğinde, onun ünsüz olduğunu tahmin etmek daha olasıdır. Ancak Markov’un asıl sorusu bu değildi. Şunu merak ediyordu: Eğer bir önceki harfi biliyorsak, bu tahmin değişir mi? Yani bir harfin ünsüz olma olasılığı, kendisinden önce gelen harfin ünlü ya da ünsüz olmasına bağlı mıdır?
Metni inceleyen Markov, bir ünsüz harfin ardından yüzde 34 oranında yine bir ünsüz, yüzde 66 oranında ise bir ünlü geldiğini buldu. Yani önceki harfi bilmek, bir sonraki harfe dair olasılıkları değiştiriyordu.
Markov ayrıca bir ünlünün ardından başka bir ünlü gelme olasılığının yalnızca yüzde 13 olduğunu hesapladı. Bu sonuçlar, Eugene Onegin’i Markov zincirine kusursuz bir örnek hâline getirdi ve Markov’un fikirlerini açıklamasını sağladı.
Sonuç Olarak
Günümüzde Markov süreçleri, bilinmeyen büyüklüklerin olasılıkla modellendiği fizik ve kimyada temel bir araçtır. Bilgi işlem alanında örüntü tanıma, otomatik konuşma çözümleme ve üretimi ile veri sıkıştırmada kullanılır. Meteoroloji, ekoloji ve biyolojide yaygın uygulamalara sahiptir.
Ayrıca sürücüsüz araçların denetiminde, makine çevirisinde, nüfus artışı, varlık fiyatları, döviz kurları ile piyasa dalgalanmalarının öngörülmesinde önemli bir rol oynar.
Kaynaklar ve ileri okumalar:
- Andrey Markov & Claude Shannon Counted Letters to Build the First Language-Generation Models. Yayınlanma tarihi: kaynak site: Bağlantı: Andrey Markov & Claude Shannon. Counted Letters to Build the First Language-Generation Models
- Andrey Markov’s Brilliant Ideas are still a Driving Force. (Erişim Tarihi: 10.03.2021); Kaynak site: Thats Math. Bağlantı: Andrey Markov’s Brilliant Ideas are still a Driving Force.
Matematiksel