1980’lerin ortalarında, Walkman’ler ve batik desenli tişörtler gibi, Mandelbrot kümesinin silueti de her yerdeydi. Öğrenciler bu görseli yurt odalarının duvarlarına astı. Matematikçiler, kümenin çıktısını isteyen yüzlerce mektup aldı. Bazıları bu ilgiye karşılık olarak kümenin en çarpıcı detaylarını kitaplara dönüştürdü.

Teknolojiye daha yakın olan meraklılar ise Ağustos 1985 tarihli Scientific American dergisine başvurdu. Derginin kapağında Mandelbrot kümesi, alevli kıvrımlarla göz alıcı bir şekilde yer alıyordu. İç sayfalarda ise bu ikonik görüntüyü bilgisayarda üretmek isteyen okuyucular için detaylı programlama talimatları vardı.
Birkaç yıl içinde, bu şekil David Hockney’nin yeni tablolarına ve bazı müzisyenlerin, Bach tarzında füg benzeri bestelerine ilham verdi. John Updike’ın kurgu eserlerinde yer buldu, edebiyat eleştirmeni Hugh Kenner’ın Ezra Pound’un şiirlerini analiz etme biçimini etkiledi. Psikedelik halüsinasyonların konusu oldu ve bilimkurgu yazarı Arthur C. Clarke’ın anlatımıyla yayımlanan bir belgesele dönüştü.
Mandelbrot Kümesi Nedir?
Mandelbrot kümesi, fraktal kenarlara sahip özel bir şekildir. Bir bilgisayar yardımıyla bu düzensiz sınırları yakınlaştırdığınızda, ne kadar derine inerseniz inin, kümenin orijinal şekline benzeyen yeni yapılarla karşılaşırsınız. Bu, sonsuz ve baş döndürücü bir öz-benzerlik zinciridir.
Bu öz-benzerlik teması, James Gleick’in çok satan Chaos (Kaos) adlı kitabında da temel bir unsurdu. Bu kitap, Mandelbrot kümesini popüler kültürde kalıcı bir yere oturtan eserlerden biri oldu.
Mandelbrot kümesi bir sembole dönüşmüştü. Çevremizi saran dünyanın fraktal doğasını tanımlamak için yeni bir matematik dili gereksinimini temsil ediyordu. En basit kurallardan nasıl olağanüstü karmaşıklıkların doğabileceğini gösteriyordu. Bir matematikçi, gençlik yıllarında Mandelbrot kümesini ilk kez keşfettiğinde, onu doğru ile yanlış arasındaki karmaşık sınırın bir metaforu olarak gördüğünü anlatmıştı.
Mandelbrot kümesinin hikâyesi bir ödülle başladı.
1915 yılında, Fransız Bilimler Akademisi bir yarışma duyurdu. Üç yıl içinde, yenileme süreci üzerine yapılacak en iyi çalışmaya 3.000 franklık büyük ödül verilecekti.
Yenileme (iterasyon), bir kuralın tekrar tekrar uygulanması anlamına gelir. Bir sayıyı bir fonksiyona yerleştirirsiniz, çıkan sonucu tekrar aynı fonksiyona giriş olarak verirsiniz. Bunu defalarca yapar ve zaman içinde ne olduğuna bakarsınız.
Bu sürecin sonucunda elde edilen sayılar bazen çok hızlı şekilde sonsuza doğru gider. Bazen de, belli bir sayıya yaklaşarak orada sabitlenir. Bazen de tamamen düzensiz bir biçimde, rastgele gibi görünen kaotik bir yol izler.

Fransız Bilimler Akademisi’ ve genel olarak matematikçiler ‘nin bu süreçle ilgilenmenin bir nedeni vardı. Bu süreç, dinamik sistemlerin incelenmesinde önemli bir role sahipti. Gezegenlerin Güneş etrafında dönmesi ya da dalgalı bir akarsuyun akışı gibi, belirli kurallara göre zaman içinde değişen sistemlerin temelinde yer alıyordu.
Ödül, iki matematikçiyi tamamen yeni bir araştırma alanı geliştirmeye yöneltti. Bunlardan ilki, sağlık sorunları asker olmasına izin vermediği için matematik ve astronomiye yönelen Pierre Fatou idi. Diğeri ise, umut vaat eden genç bir matematikçi olan Gaston Julia’ydı.
Julia’nın eğitim hayatı, I. Dünya Savaşı ve Fransız ordusuna katılması nedeniyle kesintiye uğramıştı. Henüz 22 yaşındayken, ağır bir şekilde yaralanmış ve yüzündeki hasar tedavi edilemediği için yaşamının geri kalanında yüzüne deri kayış takmak zorunda kalmıştı. Buna rağmen ödül için hazırladığı bazı çalışmaları hastane yatağında tamamladı.
Bağımsız çalıştılar, ancak ulaştıkları sonuçlar birbirine benziyordu. Bulguları o kadar çok örtüşüyordu ki, bugün bile kimin hangi fikre öncülük ettiği net değildir. (Julia daha sosyal bir kişiliğe sahipti, bu nedenle ödülü kazanan da o oldu. Fatou ise yarışmaya başvurmadı.)
Günümüzde ikisi de artık karmaşık dinamikler alanının kurucuları olarak kabul edilmektedir. “Karmaşık” terimi, Fatou ve Julia’nın karmaşık sayılar üzerinde tanımlı fonksiyonları yinelemelerinden geliyor.
Mandelbrot Kümesinin Doğuşu
Fatou ve Julia, basit görünen karmaşık fonksiyonların yinelemesinin başlangıç noktasına bağlı olarak son derece zengin ve karmaşık davranışlara yol açabileceğini keşfetmişlerdi. Fakat ardından, çalışmalarının üzeri yarım yüzyıl boyunca unutulacaktı. Neyse ki bu süreçte işin içine matematikçi Benoît Mandelbrot karıştı.
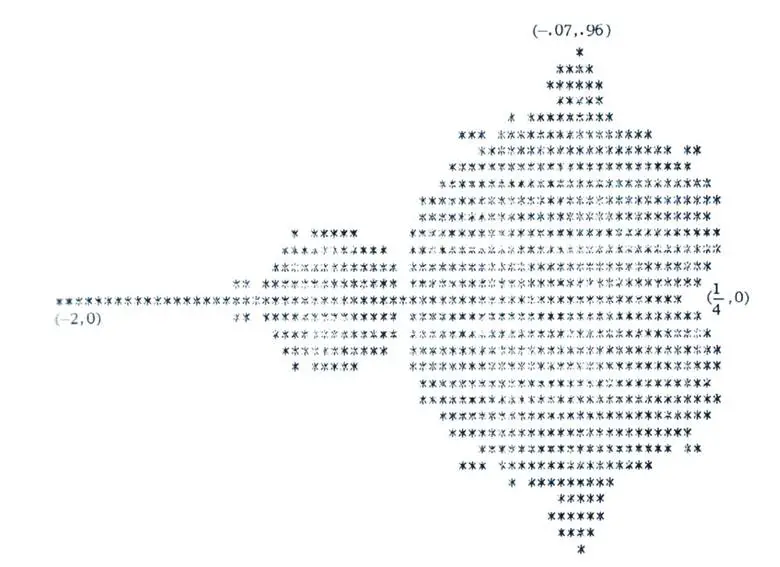
Kümenin yayımlanan ilk görseli 1978’de çıktı. Matematikçiler Robert Brooks ve J. Peter Matelski, grup teorisi ve hiperbolik geometriyle ilgili görünen başka bir konuyu incelerken, yalnızca birkaç yüz yıldız işaretinden oluşan kaba bir çizim yayımladılar.
Kümeyi popülerleştirense Benoit Mandelbrot oldu. Bilgisayar ekranında beliren görseller — bugün Julia kümeleri olarak bilinen şekiller — Mandelbrot’un gördüğü en güzel ve en karmaşık fraktal örnekler arasındaydı.
IBM’in bilgisayarlarını kullanarak yüzlerce Julia kümesi grafiği oluşturduktan sonra, hepsini aynı anda temsil etmenin bir yolunu aradı. 1980’de, Brooks ve Matelski’ye kıyasla çok daha gelişmiş bilgisayar gücüne sahipti ve Mandelbrot kümesinin çok daha iyi bir versiyonunu üretti
Mandelbrot, bu görsele âdeta âşık oldu ve fraktalı olabildiğince görünür kılmaya karar verdi. İşte bu yüzden küme onun adıyla anıldı.

Mandelbrot kümesi aslında çok basit bir denklemden doğdu: f(z) = z² + c. Burada z ve c karmaşık sayılardır. Başlangıçta z=0 alıp sonrasında denklemin çıktısını tekrar denkleme iki sonuç olur. Eğer sayılar gittikçe büyüyüp sonsuzluğa kaçıyorsa, o zaman c kümede değildir.
Eğer çıkan sayılar hep küçük kalıyorsa (bir yere “hapsoluyorsa”), o zaman seçtiğin c sayısı Mandelbrot kümesine aittir. Mandelbrot’un yaptığı şey, tek tek fonksiyonlara bakmak yerine, bütün bu fonksiyonların sonuçlarını tek bir büyük görselde birleştirmek oldu.

Sonuç Olarak
Mandelbrot kümesinin bilgisayarla üretilmiş görselleri — yukarıdaki gibi — onun inanılmaz derecede karmaşık yapısına dair ipuçları verir. Bilinen bir gerçek şudur: Kümenin sınırına ne kadar yaklaşırsanız yaklaşın, her zaman aynı derecede girintili çıkıntılı görünür.
Bu sınırın tam olarak nasıl bir yapıya sahip olduğu matematiğin açık sorularından biridir. Yine de Mandelbrot kümesi hakkında söyleyebileceğimiz çok şey var. Sonucunda onun her küçük parçası matematiksel bir anlam taşıyor.
Kaynaklar ve İleri Okumalar
- The Quest to Decode the Mandelbrot Set, Math’s Famed Fractal. Bağlantı: The Quest to Decode the Mandelbrot Set, Math’s Famed Fractal | Quanta Magazine . Yayınlanma tarihi: 26 Ocak 2024
- Unveiling the Mandelbrot set.Bağlantı: Unveiling the Mandelbrot set | plus.maths.org ; Yayınlanma tarihi: 1 Eylül 2006
- Math’s Mysterious Infinite Fractal: The Mandelbrot Set ; Video bağlantısı: https://youtu.be/u9GAnW8xFJY
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





