Kuaterniyonlar: Taşlara Yazılmış Bir Denklem Matematik Tarihini Nasıl Değiştirdi?

16 Ekim 1843’te, İrlandalı matematikçi William Hamilton, Dublin’deki Royal Canal boyunca yürürken bir aydınlanma yaşadı. Öyle heyecanlanmıştı ki, cebinden çakısını çıkarıp buluşunu oracıkta, Broome Köprüsü’ne kazıdı.

Yazdığı formül şu şekildeydi: i² = j² = k² = ijk = –1. Buluşunu “kuaterniyonlar” (dördey) olarak adlandırdı. Hamilton’un bu keşfi, matematikçilerin bilgiyi temsil etme biçimini kökten değiştirdi.

Bu fikir, köprü tasarımında kuvvetleri hesaplamaktan, MRI cihazı veya rüzgâr türbini gibi makineleri tasarlamaya, arama motorlarını programlamaktan Mars’taki bir keşif aracını yönlendirmeye kadar sayısız teknik uygulamayı kolaylaştırdı. Peki, bu ünlü formülün anlamı nedir?

Kuaterniyonlar Nedir?

Hamilton’un çözmeye çalıştığı matematiksel problem, üç boyutlu uzaydaki farklı yönler arasındaki ilişkiyi nasıl temsil edeceğiydi. Hamilton özellikle 3 boyutlu dönme hareketleriyle ilgileniyordu.

Matematikçiler, bir nesnenin konumunu x, y ve z koordinatlarıyla göstermeyi zaten biliyordu. Ancak bu koordinatların nesne döndürüldüğünde nasıl değiştiğini hesaplamak karmaşık küresel geometriler gerektiriyordu. Hamilton ise daha basit bir yöntem arıyordu. Onun esin kaynağı, iki boyutlu dönüşleri temsil etmenin olağanüstü bir yoluydu. Yani karmaşık sayılardan ilham aldı.

1800’lerin başlarında birkaç matematikçi, bir karmaşık sayının düzlem üzerindeki bir noktayla temsil edilebileceğini keşfetmişti. Ayrıca, bu yeni karmaşık düzlemde bir doğruyu 90 derece döndürmenin oldukça basit olduğunu göstermişti. Çünkü bir sayıyı i ile çarpmak, tam olarak bu dönüşü gerçekleştirir.

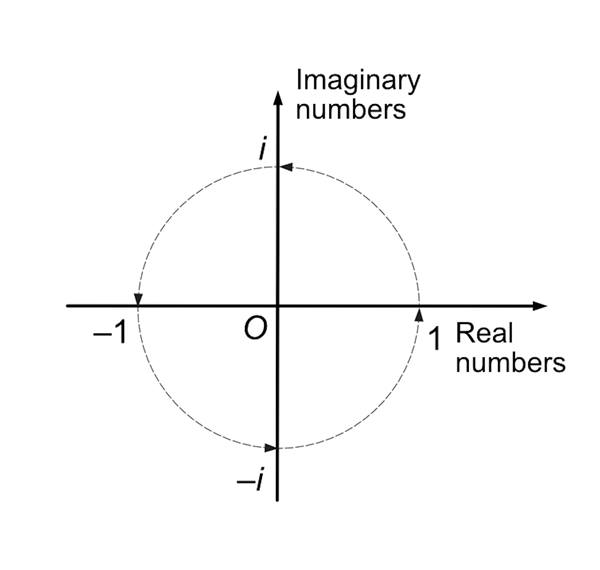
Hamilton, karmaşık sayılarla geometrinin bu bağlantısından ilham alacaktı. Bu nedenle aynı fikri üç boyuta uygulamaya karar verdi. Sonrasında üç boyutlu bir karmaşık düzlem hayal etti. Bu düzlemde, ikinci bir hayali sayı olan j’ye karşılık gelen ikinci bir eksen vardı ve bu eksen diğer ikisine dikti.

Ancak, i ile yapılan iki boyutlu dönme işlemini üç boyuta genişletmek istiyorsa, bunun yalnızca üç değil dört boyut gerektirdiğini fark etti. Bu durumda üçüncü bir hayali sayı daha tanımlaması gerekiyordu. Bu sayıyı da k olarak tanımladı.

Bu dört boyutlu matematiksel uzayda, k ekseni diğer üç eksene dik olacaktı. Ayrıca k hem k² = –1 hem de k = ij = –ji eşitliğini sağlamalıydı. (Bu iki ifadeyi birleştirdiğinizde ijk = –1 sonucu elde edilir.)

Tüm ilişkiler bir araya geldiğinde i² = j² = k² = ijk = –1 denklemi ortaya çıkar. Hamilton’un Broome Köprüsü’nde yıldırım çarpmış gibi aydınlandığı o anda keşfettiği ifade buydu.

Kuaterniyonlar Ne İşe Yarar?

Hamilton, bu dört boyutlu sayılara “kuaterniyon” adını verdi. Sonrasında da onları üç boyutlu uzayda geometrik dönüşleri hesaplamak için kullandı. Günümüzde robotların hareket ettirilmesinde ya da uyduların yönlendirilmesinde kullanılan dönüşler, işte bu yönteme dayanır.

Ancak asıl pratik güç, kuaterniyonun yalnızca hayali kısmına odaklanıldığında ortaya çıkar. Hamilton bu bölüme “vektör” adını verdi.

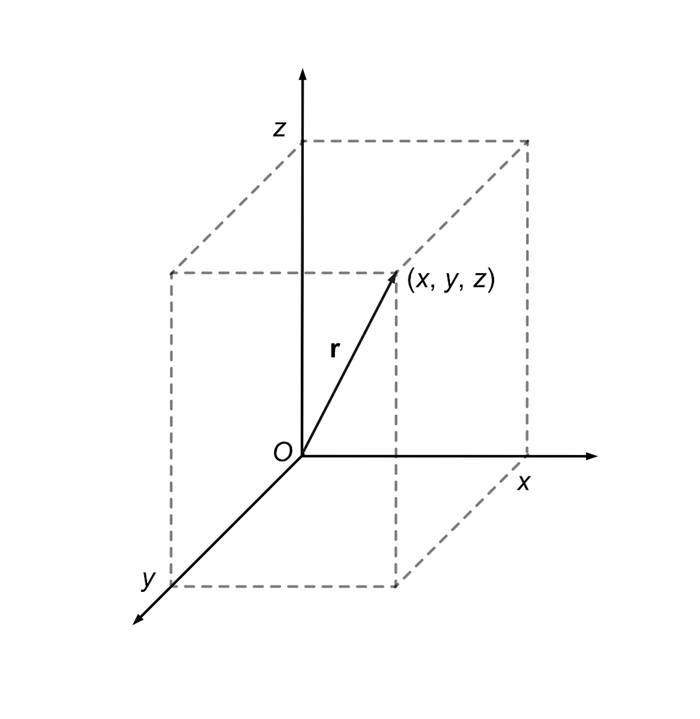
Bir vektör, iki tür bilgiyi aynı anda taşır: büyüklük ve yön. Bu, kuvvet, hız veya konum gibi uzamsal nicelikleri tanımlamanın en etkili yoludur. Örneğin bir cismin, konum eksenlerinin sıfır noktasına göre (x, y, z) konumunu göstermek için Hamilton, başlangıç noktasından cisme doğru uzanan bir ok hayal etti. Bu ok, konum vektörü olarak tanımlanan x i + y j + z k ifadesine karşılık gelir.

Yarım yüzyıl sonra, İngiliz Oliver Heaviside, Hamilton’un i, j, k biçimindeki hayali çerçevesini gerçek birim vektörlerle değiştirerek modern vektör analizinin temelini attı. Ancak hangi gösterim kullanılırsa kullanılsın, vektörün bileşenleri aynı kaldı. Dolayısıyla oku temsil eden yön ve vektör çarpımının temel kuralları da değişmedi.

Hamilton, vektörleri çarpmak için iki farklı yöntem tanımladı. Bunlardan ilki bir sayı üretir; bugün buna skaler çarpım ya da noktasal çarpım diyoruz. İkincisi ise yeni bir vektör ortaya çıkarır. Bu da vektörel çarpım ya da çapraz çarpımdır. Hamilton’un tanımladığı bu çarpım biçimleri, modern fiziğin ve mühendisliğin yapıtaşlarından biri haline geldi.

Hamilton ayrıca denklemlerini daha kısa ve estetik hale getirmek için özel bir gösterim geliştirdi. Örneğin, elektrik ve manyetik alanlar arasındaki ilişkiyi tanımlayan Maxwell denklemlerinden biri şöyle yazılır: ∇ × E = –∂B/∂t. Yalnızca birkaç sembolle bu denklem, elektrik alan vektörü E’nin, manyetik alan vektörü B’deki değişimlere karşı uzayda nasıl yayıldığını gösterir.

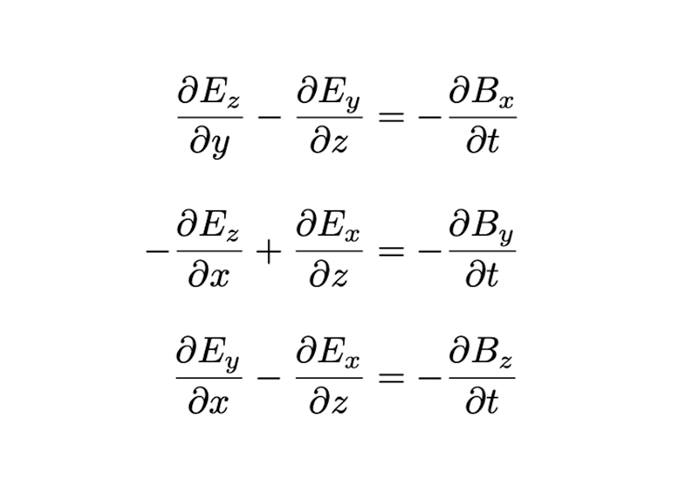
Vektör gösterimi olmasaydı, bu ilişkiyi açıklamak için B ve E’nin her bileşeni için üç ayrı denklem yazmak gerekirdi. Elbette her biri koordinatlar, çarpımlar ve farklarla dolu karmaşık ifadeler olurdu.

Sonuç Olarak

Hamilton bugün yaşasaydı, vektörlerin bu kadar yaygın kullanılmasından büyük bir mutluluk duyardı. Üstelik vektörler artık yalnızca fiziksel değil, dijital bilgileri de temsil edebiliyor. Ancak onu en çok sevindirecek şey, döndürme işlemlerinin programlanmasında hâlâ en etkili yöntemin kuaterniyonlar olması olurdu.

Hamilton’un başarısını anmak için her yıl 16 Ekim’de matematik meraklıları, onun Dublin’deki ünlü yürüyüşünü yeniden canlandırır. Ama gerçekte, o sade görünümlü formülün meyvelerini biz her gün, modern teknolojinin hemen her alanında kullanıyoruz.

---

Kaynaklar ve ileri okumalar:

• Three letters, one number, a knife and a stone bridge. How a graffitied equation changed mathematical history. Kaymak site: Conversation. Yayınlanma tarihi: 15 Ekim 2024. Bağlantı: Three letters, one number, a knife and a stone bridge

Matematiksel