Henri Lebesgue, integral kavramını kökten değiştirerek matematiğe yeni bir boyut kazandırdı. Riemann yöntemlerinin yetersiz kaldığı karmaşık fonksiyonları da kapsayabilen Lebesgue integrali, matematiksel analizi çok daha güçlü ve kapsamlı bir yapıya dönüştürdü.

İntegral, bir fonksiyonun grafiğiyle x ekseni arasında kalan alanı hesaplamanın temel yöntemidir. Genellikle x = a ile x = b arasındaki aralıkta, eğrinin altında kalan alanı bulmak isteriz. Bu iki nokta, integralin sınırlarını oluşturur.
İşlem şöyle işler: x eksenindeki bu aralığı küçük parçalara böler, her bir parçada fonksiyonun değeri kadar yüksekliğe sahip dikdörtgenler oluştururuz. Bu dikdörtgenlerin alanlarını topladığımızda, grafiğin altındaki alanın yaklaşık değerine ulaşırız.
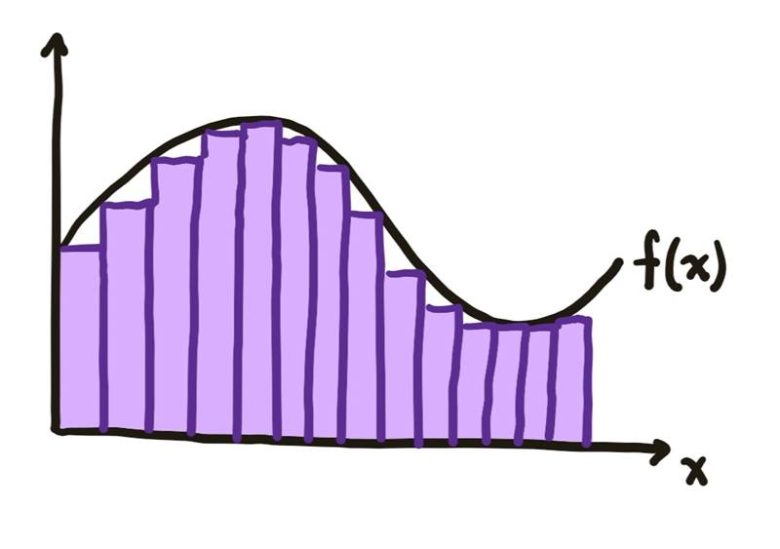
Ancak bu yalnızca yaklaşık bir yöntemdir. Gerçek değeri elde etmek için, dikdörtgenlerin genişliğini giderek küçültür, teorik olarak sıfıra yaklaştırırız. Genişlik sıfıra yaklaştıkça, toplam alan grafiğin altını tam olarak kapsar. İşte bu sınır değeri — yani sonsuz sayıda, sonsuz incelikte dikdörtgenin alanlarının toplamı — integrali tanımlar.
Sonlu sayıda dikdörtgenle yapılan bu yaklaşık hesaplama, Riemann integrali olarak adlandırılır. Ancak bu yöntem, çok karmaşık ya da düzensiz fonksiyonlarda yetersiz kalır. Bu sınırlamayı aşmak için daha soyut ve kapsamlı bir ölçüm yaklaşımına ihtiyaç doğdu. Bu yaklaşımı geliştiren kişi Henri Léon Lebesgue oldu.
Henri Léon Lebesgue Kimdir? (1875–1941)

Henri Lebesgue, 1875 yılında Fransa’nın Beauvais kentinde doğdu. Henüz üç yaşındayken babasını ve iki kız kardeşini veremden kaybetti. Annesi, tüm zorluklara rağmen onun iyi bir eğitim alması için büyük fedakârlık gösterdi. Lebesgue’in yeteneği daha ilkokuldayken öğretmenlerinin dikkatini çekti.
Aldığı bursla Paris’teki seçkin liselerden birine, ardından École Normale Supérieure’e kabul edildi. Bu okul, Henri Poincaré ve Évariste Galois gibi matematik tarihine yön veren isimleri yetiştirmişti. Lebesgue de burada matematiksel yetkinliğini derinleştirdi.
1902’de tamamladığı doktora tezi Intégrale, Longueur, Aire (İntegral, Uzunluk, Alan), yalnızca bir akademik çalışma değil, matematikte çığır açan bir dönüm noktasıydı. Bu tezde, klasik Riemann integralinin sınırlarını aşan ve çok daha genel fonksiyonları kapsayan Lebesgue integralini geliştirdi.
1910’da Sorbonne’a geçti, 1921’de ise Fransa’nın en saygın kurumlarından Collège de France’ta profesör oldu. Aynı zamanda 1937’ye kadar École Normale Supérieure’de ders vermeye devam etti.
Lebesgue İntegrali Nedir?
Antik Yunan’da Arşimet, belirli eğrilerle sınırlı alanları ölçmeye çalıştı. Özellikle parabol altındaki alanları hesaplamak için son derece yaratıcı yöntemler geliştirdi. 17. yüzyılda Isaac Newton ve Gottfried Wilhelm Leibniz, bir eğrinin altındaki alanı bulma problemiyle (integral), eğriye teğet çizme problemini (türev) ilişkilendirerek kalkülüsün temellerini attı.
Augustin Cauchy, bu fikirleri tanımlayıp ispatlayarak matematiğe sağlam bir çerçeve kazandırdı. Ardından Bernhard Riemann, bir fonksiyonun integrallenebilirliğini kesin biçimde tanımladı.
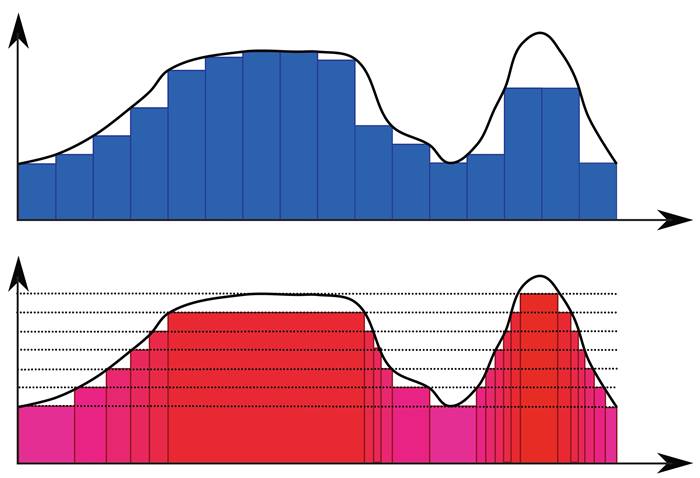
Riemann, fonksiyonun tanım kümesini esas aldı. x ekseni boyunca küçük aralıklar seçti; her aralıkta fonksiyonun değerini kullanarak dikdörtgenler oluşturdu. Bu dikdörtgenlerin alanlarını toplayarak, grafiğin altındaki alanı yaklaşık olarak hesapladı.
Henri Lebesgue ise farklı bir yaklaşım benimsedi. Tanım kümesi yerine değer kümesini temel aldı. Önce y eksenini küçük aralıklara ayırdı, ardından her y aralığına karşılık gelen x değerlerinin toplam uzunluğunu hesapladı.
Her y değeri için, bu değere karşılık gelen x’lerin oluşturduğu genişliğe ulaştı. Dikdörtgenlerin yüksekliğini y aralıkları, genişliğini ise bu x uzunlukları belirledi. Bu yöntem, yalnızca düzenli fonksiyonlar için değil, karmaşık ve düzensiz yapılar için de integral hesaplamayı mümkün kıldı.
Lebesgue İntegrali Neden Önemlidir?
Riemann integraliyle ölçülebilen her fonksiyon, Lebesgue integraliyle de ölçülür. Ancak bazı “yaramaz” fonksiyonlar vardır ki, yalnızca Lebesgue yaklaşımıyla ele alınır. Örneğin, [0, 1] aralığındaki tüm rasyonel sayılardan oluşan bir dikdörtgen düşünelim. Sonucunda bu alanı geleneksel yöntemlerle ölçmek ve bu tür kümelere Riemann integraliyle ölçü atamak imkânsızdır.

Lebesgue’un geliştirdiği güçlü ölçüm araçları sayesinde, soyut kümelere de anlamlı ölçüler atanır. Böylece yalnızca daha karmaşık fonksiyonları kapsamakla kalmayan, aynı zamanda matematiksel olarak daha doğal ve sağlam temellere dayanan bir integral kuramı ortaya konmuş olur.
Lebesgue’nin doktora tezi, matematikte yalnızca yeni bir integral tanımı sunmakla kalmadı. Ayrıca ölçü kuramı adı verilen yeni bir alanın başlangıcını oluşturdu. Bu kuramın gelişimi, yalnızca matematiksel analizi değil, olasılık teorisinin temel yapılarını da derinden etkiledi. 1930’lara gelindiğinde, ölçü kavramı olasılık kuramında doğal ve vazgeçilmez bir yere sahipti.
Diyelim ki birkaç piyango bileti aldık ve kazanan numaraların açıklanmasını bekliyoruz. Tüm piyango biletlerinin oluşturduğu küme, olasılık uzayımızı temsil eder. Elimizdeki biletler ise bu uzayın bir alt kümesidir. Kazanan biletin bizde olma olasılığı, bu alt kümenin ölçüsüdür.
Modern olasılık kuramı bu düşünce üzerine kuruludur. Nasıl ki uzunluk, doğru üzerindeki alt kümelere ölçü atayan bir kavramsa, olasılık da olası sonuç kümelerine ölçü atayan bir yöntemdir.
Sonuç Olarak
Fransız matematikçi Paul Montel, Henri Lebesgue için kaleme aldığı ölüm ilanında onu şöyle tanımlar. “O, büyük bir bilge, hayranlık uyandıran bir öğretmen ve eşi benzeri olmayan bir ahlaki soyluluğa sahipti. Matematik üzerindeki etkisi, hem kendi çalışmalarıyla hem de ilham verdiği eserlerle uzun süre devam edecektir.”
Kaynaklar ve ileri okumalar
- Der Mathematische Monatskalender:Henri Léon Lebesgue. Kaynak site: Bağlantı: Der Mathematische Monatskalender:Henri Léon Lebesgue
- Prof Henri-Léon Lebesgue, For, Mem R.S. Nature 133, 714 (1934). https://doi.org/10.1038/133714b0
- Axler, Sheldon. (2020). Measures. 10.1007/978-3-030-33143-6_2.
- Maths in a minute: Measure. Kaynak site: Plus Math: Yayınlanma tarihi: 7 Ağustos 2024. Bağlantı: Maths in a minute: Measure
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





