Kitaplığınızı düzenlemenin tek bir en iyi yolu olmadığı gibi, bilgiyi depolamanın da herkese uyan tek bir çözümü yoktur. Veri yapılarının ardındaki matematik, farklı depolama yaklaşımlarının zaman, bellek ve diğer kaynaklar arasında neden zorunlu ödünler içerdiğini daha açık biçimde görmemizi sağlar. Bu süreçte hash tabloları, hangi veriye ne zaman ihtiyaç duyulacağını önceden kestirmenin zor olduğu durumlarda hızlı erişim sunan etkili bir çözüm olarak öne çıkar.

Yeni bir dijital dosya oluşturduğunuzda bilgisayar bu dosya için hızla uygun bir yer bulur. Daha sonra dosyayı silmek istediğinizde doğru bitleri hızla tespit eder ve kaldırır. Araştırmacılar, veri yapıları adı verilen depolama sistemlerini tasarlarken veriyi ekleme süresi, silme süresi ve sistemin kullandığı toplam bellek miktarı arasında dengeli bir yapı kurmayı hedefler.
Bu durumu daha iyi anlamak için tüm kitaplarınızı tek ve uzun bir rafa dizdiğinizi düşünün. Kitapları alfabetik sıraya koyarsanız aradığınız kitabı kolayca bulursunuz. Ancak yeni bir kitap aldığınızda doğru yeri bulup yerleştirmek zaman alır.
Buna karşılık kitapları rafta bulduğunuz ilk boşluğa yerleştirirseniz başlangıçta zaman kazanırsınız. Fakat bir süre sonra aradığınız kitabı bulmak giderek zorlaşır. Ekleme süresi ile erişim süresi arasındaki bu ödünleşim küçük bir kütüphane için sorun yaratmaz. Ancak kitap sayısı binlere ulaştığında ciddi bir probleme dönüşür.
Uzun bir raf yerine, alfabetik olarak etiketlenmiş 26 kutu ile kitapları yazarların soyadlarının ilk harfine göre bu kutulara yerleştirebilirsiniz. Yeni bir kitap aldığınızda hangi kutuya koyacağınızı hemen bilirsiniz. Bir kitabı aradığınızda ise doğrudan doğru kutuya yönelirsiniz.

Bu yöntem, bazı durumlarda kitapları tek ve uzun bir rafta saklamaya kıyasla ekleme ve çıkarma işlemlerini çok daha hızlı yapmanızı sağlayacaktır. Ancak bu kutu sistemi de kendi sorunlarını doğurur. Her kutuda yalnızca tek bir kitap varsa, aradığınız kitaba gerçekten anında ulaşırsınız. Aksi halde doğru kitabı aramak zorunda kalırsınız.
Hash Tabloları Nedir?
Uç bir senaryoda, tüm kitaplarınız aynı harfle başlayan yazarlara aitse yeniden tek ve uzun raf sorunuyla karşılaşırsınız. Ayrıca etrafta yer kaplayan çok sayıda boş kutu bulundurursunuz. Bilgisayar bilimciler, bu basit kutu sisteminin daha gelişmiş bir karşılığı olan hash tablolarını sıkça inceler.
Hash tabloları, her öğe için anahtar adı verilen bilinen bir özelliği kullanarak bir depolama adresi hesaplar. Bu örnekte her kitabın anahtarı, yazarın soyadının ilk harfidir.
Ancak bu kadar basit bir anahtar seçimi, bazı kutuları diğerlerinden çok daha dolu hale getirir. Örneğin İngilizce yazan yazarlar arasında soyadı X harfiyle başlayanların sayısı oldukça azdır. Daha etkili bir yaklaşım, yazarın tam adını temel alır.
Bu yöntemde adın her harfini alfabedeki sırasına karşılık gelen bir sayıya dönüştürürsünüz. Ardından bu sayıları toplar ve toplamı 26’ya bölersiniz. Kalan değer sıfır ile 25 arasında bir sayı üretir. Bu sayı, kitabı hangi kutuya yerleştireceğinizi belirler.
Bir anahtarı depolama adresine dönüştüren matematiksel kurala hash fonksiyonu denir. Bir hash fonksiyonu, öğeleri kutular arasında mümkün olduğunca dengeli dağıtır. Böylece her kutuda arama yaparken daha az zaman harcarsınız.
Bir öğeye daha hızlı ulaşmak için kutu sayısını artırabilirsiniz. Ancak bu tercih yeni bir sorun yaratır. Bazı kutular boş kalsa bile bellekte yer kaplar. Alan ile zaman arasındaki bu denge, hash tablolarının temel bir özelliğini oluşturur. Ekleme ve erişim süresi arasındaki gerilimi azaltmak için bu bedeli ödersiniz.
Hash tabloları, bir sonraki adımda hangi veriye ihtiyaç duyacağınızı öngöremediğiniz durumlarda iyi çalışır. Ancak her zaman en uygun çözümü sunmazlar. Farklı teslim tarihleri olan görevleri sürekli eklediğiniz bir yapılacaklar listesi üzerinde çalıştığınızı düşünün. Yeni görevleri hızla eklemek istersiniz. Buna karşılık görevleri yalnızca en acil hâle geldiklerinde geri çağırırsınız.
Bu tür durumlarda en uygun çözüm, heap adı verilen veri yapısıdır. Heap, veriyi düzenli bir sıra yerine daha dağınık bir biçimde saklar. Bazı öğeler diğerlerinin üzerinde yer alır ve üstte bulunanlara daha kolay erişirsiniz.
İkili Ağaç Sistemi Nedir?
En yüksek önceliğe sahip öğe her zaman yığının en üstünde bulunur. Alt katmanlar ise daha düzensiz bir yapı gösterir. Ancak düşük öncelikli öğelerin kendi aralarındaki konumu önem taşımadığı için bu düzensizlik sorun yaratmaz. Bu temel fikrin en basit uygulaması, ikili ağaç adı verilen matematiksel yapıyı kullanır.
İkili ağaç, belirli bir düzeni olan düğümlerden oluşur. En üstte tek bir düğüm yer alır ve her düğüm doğrudan altındaki iki düğüme bağlanır.
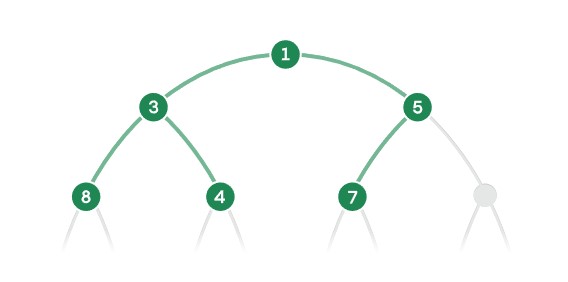
Bir yapılacaklar listesindeki öğeleri bu yapıda sakladığınızı düşünün. Her düğüm tek bir öğe tutar ve her öğeyi teslim tarihini temsil eden bir sayıyla etiketlersiniz. Önceliği yüksek olan öğelere daha küçük sayılar verirsiniz. Böylece en acil işler ağacın üst kısımlarında toplanır ve onlara daha hızlı erişirsiniz.
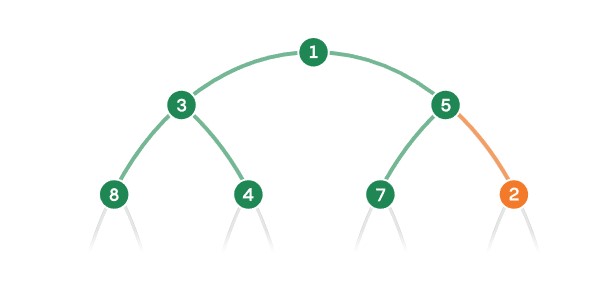
Her yeni öğeyi ağacın en alt düzeyindeki ilk boş konuma yerleştirirsiniz. Ardından yeni öğenin teslim tarihini doğrudan üstündeki düğümle karşılaştırırsınız. Eğer yeni görev daha erken bir tarihe sahipse, yani daha yüksek öncelik taşıyorsa, iki öğenin yerini değiştirirsiniz.
Bu karşılaştırma ve yer değiştirme işlemini, yeni öğe kendisinden daha acil bir öğenin hemen altına yerleşene kadar sürdürürsünüz.
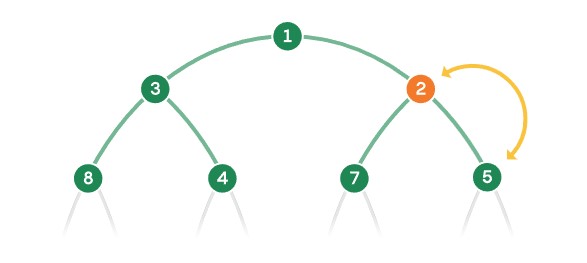
Bu yöntem, en yüksek önceliğe sahip öğeyi her zaman en üste taşır. Yapılacaklar listenizde bin görev bulunsa ve sürekli yeni görevler eklense bile, her yeni öğe doğru konumuna ulaşmak için en fazla dokuz kez yer değiştirir.
Sonuç Olarak
Eşyaları en iyi nasıl düzenlemeniz gerektiği konusunda birbiriyle çelişen öneriler sunan sayısız kişisel gelişim kitabı vardır. Bilgisayar biliminin verdiği temel ders ise nettir: Kusursuz tek bir çözüm yoktur. Her yaklaşım belirli ödünler gerektirir. Sizin için bazı ölçütler daha önemliyse, biraz dağınıklığı kabullenirsiniz.
Kaynaklar ve ileri okumalar
- Why There’s No Single Best Way To Store Information. Kaynak site: Quanta Magazine. Yayınlanma tarihi: Bağlantı: Why There’s No Single Best Way To Store Information
- Bento, Lucila & Pereira de Sá, Vinícius & Szwarcfiter, Jayme. (2015). Some illustrative examples on the use of hash tables. Pesquisa Operacional. 10.1590/0101-7438.2015.035.02.0423.
Platformumuzun sürdürülebilirliğini, sitemizde yayımlanan reklam gelirleriyle sağlamaktayız. Yüksek erişim ve içerik kalitesini koruyan bir dijital yayıncılık faaliyetini sürdürmek önemli maliyetler gerektirmektedir. Bu konuda göstereceğiniz anlayış için teşekkür ederiz. Yayınlarımızı paylaşarak platformumuzun büyümesine katkı sunabilirsiniz. Matematikle kalın, bilimle kalın.
Matematiksel