The Melancholy of Haruhi Suzumiya adını daha önce duymamış olabilirsiniz; ancak anime hayranları için özel bir yere sahiptir. Hikâye, bir lise öğrencisi olan Kyon’un gözünden anlatılır. Eksantrik arkadaşı Haruhi’nin ısrarıyla, Kyon kendini birbirinden tuhaf maceraların içinde bulur. 2003’te başlayan bu serüven, bugüne kadar 10 ek roman, bir film uyarlaması, birkaç video oyunu ile genişleyerek bir fenomene dönüşmüştür.

16 Eylül 2011’de bir anime hayranı, 4chan adlı forumda bir gönderi paylaştı. Zaman yolculuğunu konu alan dizinin ilk sezonu kronolojik olmayan bir sırayla yayınlanmıştı. Yeniden yayınlanan sürüm ve DVD versiyonu da bölümlerin sırasını farklı biçimde düzenlemişti.
Hayranlar çevrimiçinde en iyi izleme sırasını tartışırken, 4chan kullanıcısı şu soruyu ortaya attı. İzleyiciler diziyi tüm olası sıralamalarla izlemek isteselerdi, en kısa kaç bölümlük bir liste izlemeleri gerekirdi?
Bir saatten kısa bir süre içinde anonim bir kullanıcı yanıt verdi. Tam bir çözüm değil, ama gerekli bölüm sayısı için bir alt sınır sundu. Herhangi bir uzunluktaki dizi için geçerli olan bu argümana göre, Haruhi’nin 14 bölümlük ilk sezonunu tüm olası sıralarda izlemek isteyenlerin en az 93.884.313.611 bölüm izlemesi gerekiyordu.
Bu kanıt matematik camiasının dikkatinden yedi yıl boyunca kaçtı. O dönemde yalnızca bir profesyonel matematikçi sorunun önemini fark etti ama o da detaylıca incelemedi. Ancak daha sonra bilimkurgu yazarı Greg Egan, gerekli bölüm sayısı için bir üst sınır kanıtladı.
Egan’ın keşfi, hem bu probleme olan ilgiyi tazeledi hem de 2011’deki paylaşımı yeniden gündeme taşıdı. Matematikçiler kısa sürede Egan’ın üst sınır kanıtını doğruladı. Bu kanıt, alt sınır gibi, herhangi bir uzunluktaki dizilere uygulanabiliyordu. Bugün her iki kanıt da bu bulmacada önemli ilerlemeler olarak kabul ediliyor.
Süperpermütasyonlar ve Haruhi Problemi
Matematikte permütasyon, bir kümenin elemanlarının kaç farklı sırayla dizilebileceğini gösterir. Örneğin {2, 7} kümesi için iki farklı permütasyon vardır: (2, 7) ve (7, 2). Bu örnekte yalnızca iki eleman olduğu için hem maksimum hem de minimum permütasyon sayısı aynıdır. Ancak Haruhi Suzumiya problemi, çok daha karmaşık bir yapıdadır.
14 bölümü tüm olası sıralarla izleyebilmenin ve bunu en az sayıda bölümle yapabilmenin yolu, basit permütasyonlardan değil, süperpermütasyon adı verilen özel bir çözümden geçer. Süperpermütasyon, bir kümenin tüm olası permütasyonlarını tek bir dizilim içinde barındıran özel bir sıralamadır. Buradaki esas amaç ise, bu sıralamanın mümkün olan en kısa hâlini, yani minimum süperpermütasyonu bulmaktır.

Bir televizyon dizisi yalnızca üç bölümden oluşsa, bu bölümleri izlemenin altı farklı sırası vardır: 123, 132, 213, 231, 312 ve 321. Bu altı sıralamayı arka arkaya dizerseniz, her olasılığı kapsayan 18 bölümlük bir liste elde edersiniz. Ama çok daha verimli bir yol vardır: 123121321. Bu tür diziler, n tane sembolün tüm permütasyonlarını içeren en kısa düzeni verir. Bu da bize unlara “süperpermütasyonı” verir.
1993’te Daniel Ashlock ve Jenett Tillotson, farklı n değerleri için en kısa süperpermütasyonlara baktıklarında ilginç bir desen fark ettiler. Bu desen, faktöriyellerle bağlantılıydı.
Eğer diziniz yalnızca tek bölümden oluşuyorsa, en kısa süperpermütasyonun uzunluğu 1!’dir (yani sadece 1). İki bölümlük bir dizi için en kısa süperpermütasyon 121 olur ve uzunluğu 2! + 1!’dir. Üç bölüm için uzunluk 3! + 2! + 1!’dir. Dört bölüm için (örneğin 123412314231243121342132413214321) uzunluk 4! + 3! + 2! + 1!’dir.
Bu kural, uzun süre matematikçiler arasında genel kabul gördü. Her n için kanıtlanamamış olsa da n = 5 için doğruluğu sonradan ispatlandı.
Nathaniel Johnson aslında bir anime hayranı değildi. Ancak 2013’te süperpermütasyonlarla ilgili terimleri araştırırken Haruhi Suzumiya problemine dair tartışmayı fark etti ve bir blog yazısı kaleme aldı. Bu yazı uzun süre fazla ilgi görmedi. Ancak 2018’de matematikçi Robin Houston’ın dikkatini çekence işler değişti.
Matematikçiler Haruhi Problemini Nasıl Çözdü
Bunun üzerine Houston, meslektaşları Jay Pantone ve Vince Vatter ile birlikte çalışarak 4chan’da başlayan bu tartışmayı akademik bir makaleye dönüştürdü. Üstelik makalelerinde ilk yazar olarak “Anonymous 4chan Poster” adını kullanarak anonim yazara da hakkını verdiler.
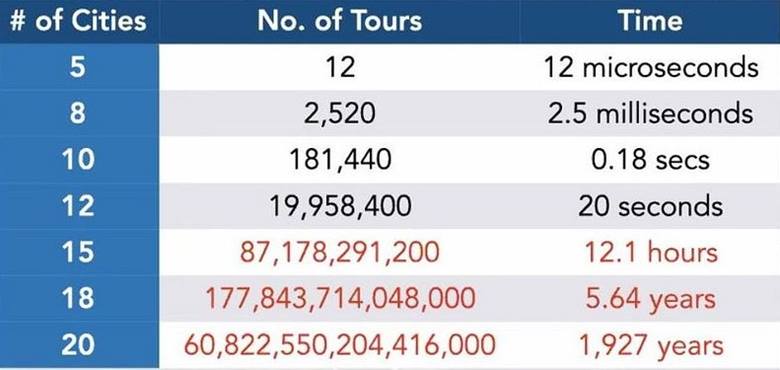
2014’te Houston, n = 6 için beklenmedik bir sonuç bularak matematikçileri şaşırttı. Faktöriyel kuralı, altı bölümü tüm olası sıralarla izlemek için 873 bölüm gerektiğini öngörüyordu. Ancak Houston bunu 872 bölümde yapmanın bir yolunu gösterdi. Houston’un yöntemi, süperpermütasyon problemini ünlü gezgin satıcı problemine çevirmeye dayanıyordu.
Bu problemde bir kişinin farklı şehirleri gezip en sonunda kendi şehrine dönmesi gerekir. Amaç, tüm şehirleri birbirine bağlayan en kısa rotayı bulmaktır. Daha özelinde, süperpermütasyonlar asimetrik gezgin satıcı problemine karşılık gelir. Burada iki şehir arasındaki yolun bir maliyeti vardır ve bu maliyet iki yönde aynı olmak zorunda değildir. Hedef, tüm şehirlerden geçerken en az maliyetli rotayı bulmaktır.
Çeviri fikri basittir: Her permütasyonu bir “şehir” gibi düşünün ve her birinden diğerine bir yol olduğunu hayal edin. Süperpermütasyon probleminde amacımız, tüm permütasyonları içeren en kısa sayı dizisini elde etmektir.
Yani hedef, her yeni permütasyona mümkün olduğunca az rakam ekleyerek ilerlemektir. Bu yüzden her yolun maliyetini, ikinci permütasyonu oluşturmak için ilk permütasyona eklememiz gereken rakam sayısı olarak tanımlarız. Örneğin n = 3 için:
- 231’den 312’ye gitmenin maliyeti 1’dir, çünkü yalnızca sonuna bir “2” eklemek yeterlidir: 231 → 312.
- 231’den 132’ye gitmenin maliyeti 2’dir, çünkü bu kez sonuna “32” eklememiz gerekir: 231 → 132.
Bu şekilde tanımlandığında, şehirler arasındaki en ucuz rota doğrudan en kısa süperpermütasyona karşılık gelir. Ancak burada büyük bir sorun var. Gezgin satıcı problemi NP-zor problem olarak bilinir; yani tüm durumlarını verimli şekilde çözen bir algoritma yoktur.
Ancak bazı durumlarda yaklaşık çözümler üreten yöntemler vardır. Houston da bu sayede kullanarak 872 basamaklı süperpermütasyonu elde etti. Fakat bu yalnızca yaklaşık bir çözümdür; yani gerçekten en kısa süperpermütasyon olmayabilir.
Sonuç olarak

Süperpermütasyonlar, hâlen çözülmemiş bir matematik problemi olarak varlığını sürdürüyor. Sonuç olarak, Haruhi Suzumiya’nın ilk sezonunu tüm olası sıralarla izlemek için yaklaşık 93,9 milyar bölüm gerekiyor. Matematikçiler sayıyı biraz daha düşürse bile, fark en fazla 40 milyon bölüm olacak.
Kaynaklar ve ileri okumalar
How an Anonymous 4chan Post Helped Solve a 25-Year-Old Math Puzzle. Kaynak site: Wired. Yayınlanma tarihi: Bağlantı: How an Anonymous 4chan Post Helped Solve a 25-Year-Old Math Puzzle
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






