Herhangi bir topun tüm yüzeyinin tüylerle kapladığınızı düşünün. Şimdi elinize bir tarak alarak bu topun üzerindeki tüyleri taramaya çalışın. Bunu yaparsanız mutlaka bir yerlerde taranmamış bir “tutam” kalır. Bu oldukça tuhaf görünen iddia—“Saçlı ya da tüylü top teoremi”—aslında topoloji adı verilen matematik dalının ciddi bir sonucudur. Ayrıca, bu teoremin meteoroloji, radyo iletişimi ve nükleer enerji gibi alanlarda önemli uygulamaları vardır.

Saçlı Top Teoremi Nedir?
Buradaki “tutam”, ya bir boşluk (kel nokta) ya da düzleşmeyen, yukarı doğru dikilmiş bir saç parçası anlamına gelir. Elbette matematikçiler bu problemi “saç” terimiyle açıklamaz. Teknik anlatımla: Top bir küre, üzerindeki saçlar ise vektör olarak düşünülür.
“Saçı” düzgün taramak demek, kürenin yüzeyine tam olarak bir noktadan değen yani “teğet” vektörler dizmek anlamına gelir. Ayrıca tarama işlemi düzgün olmalıdır; yani saçlar (vektörler) aniden yön değiştirmemeli, yumuşak geçişlerle yön değiştirmelidir. Kısacası, bu vektörlerin tüm yüzeye kesintisiz ve düzgün bir şekilde yayılması gerekir.
İşte bu şartlar bir araya geldiğinde, teorem şunu söyler: Böyle bir vektör düzenlemesi mutlaka bir yerde bozulacaktır. Ya bir vektör sıfır uzunlukta olacak (kel nokta), ya vektör yüzeye teğet olmayacaktır. Matematiksel ifadesiyle: “Bir küre üzerinde kesintisiz, sıfırdan farklı ve her noktada teğet olan bir vektör alanı oluşturmak mümkün değildir.”

Topoloji alanında matematikçiler şekilleri, tıpkı geometride olduğu gibi inceler ama bu şekilleri sanki sonsuz esnekliğe sahip bir lastikten yapılmış gibi düşünürler. Bu lastik şekil değiştirebilir ama yırtılamaz, birleşemez ve kendi içinden geçemez. Eğer bir şekil bu kuralları ihlal etmeden başka bir şekle dönüşebiliyorsa, topolojide bu iki şekil eşdeğerdir..
Bu da demektir ki, saçlı top teoremi; tüylü pelüş oyuncaklar ve hatta beyzbol sopaları için de geçerlidir. Çünkü bunların hepsi, topolojik olarak bir küreyle aynı sınıftadır. Bir parça oyun hamurunu ezip bükerek bu nesnelerin hepsini oluşturabilirsiniz.
Saçlı Top Teoremi Nerede Karşımıza Çıkar?
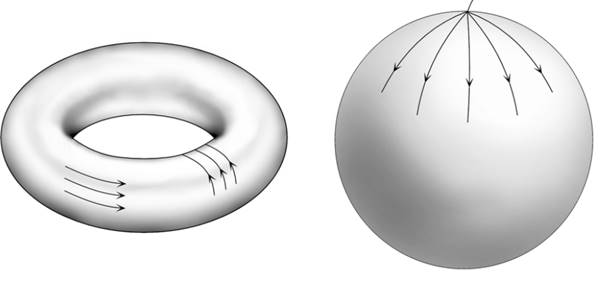
Ama bazı şekiller küreyle eşdeğer değildir. Örneğin simit şekli (torus), küreyle aynı değildir. Dolayısıyla tüylü bir simit (ne kadar iştah kaçırıcı olsa da) düzgünce taranacaktır.
Bu şartlar, teoremin koşullarını karşılar. Dolayısıyla akış bir yerde bozulmalı, yani rüzgâr durmalıdır. Bu durma noktası, bir fırtınanın gözü ya da rüzgârın doğrudan yukarı esmesi gibi bir durumda gerçekleşir.
Saçlı top teoreminin şaşırtıcı sonuçlarından biri şudur. Dünya üzerinde mutlaka bir yerde rüzgârın esmediği bir nokta vardır. Rüzgâr, yüzey boyunca sürekli bir akış halinde hareket eder. Bu akış, küre üzerinde teğet vektörlerle modellenir. (Bu vektörlerin uzunluğu fiziksel saç tellerine benzemek zorunda değildir.)

Teoremin bir başka ilginç sonucu da dönen nesnelerdedir. Örneğin bir basketbol topunu istediğiniz gibi çevirin. Topun yüzeyinde mutlaka hızı sıfır olan bir nokta olacaktır.
Her noktaya yön ve hız değerine göre bir teğet vektör atanır. Dönme hareketi süreklidir, bu nedenle teorem burada da geçerlidir ve sıfır hızda bir nokta olacağını garanti eder. Bu kulağa açık gibi gelebilir. Sonucunda dönme ekseninin uç noktaları hareket etmez.
Peki, topu eksen boyunca delip bu hareketsiz noktaları ortadan kaldırsak ne olur? Artık her nokta hareket ediyor gibi görünür. Teoreme aykırı mı olurduk? Hayır, çünkü topu deldiğimizde onu bir simite, yani torusa çevirmiş oluruz. Ve simitler bu teoremin dışında kalır.
Saçlı Top Teoremi Ne İşe Yarar?
Bu eğlenceli örneklerin ötesinde, saçlı top teoremi mühendislikte de somut kısıtlar getirir. Radyo mühendisliği buna iyi bir örnektir. Antenler, tasarıma bağlı olarak radyo dalgalarını çeşitli yönlere yayar. Bazı antenler sinyali belli bir yöne yoğunlaştırırken, bazıları daha geniş bir alana yayar. Teorik olarak “her yöne eşit güçte sinyal yayan” bir anten (izotropik anten) tasarlamak cazip gelir.. Ancak topoloji buna engel olur.
Kaynaktan uzaklaştıkça, radyo dalgaları üzerindeki elektrik alan, hareket yönüne dik bir yapıya sahiptir—yani küreye teğett olur. Bu da saçlı top teoremini devreye sokar. Alanın bir noktada sıfıra düşmesi gerekir; bu da antenin sinyalinde bir kesinti olacağı anlamına gelir. Bu yüzden izotropik antenler yalnızca teoride var olan referanslardır. Öte yandan, ses dalgaları bu diklik özelliğine sahip olmadığı için hoparlörlerin sesi her yöne eşit yayması mümkündür.
Belki de saçlı top teoreminin en “havalı” uygulaması nükleer füzyon enerjisindedir. Füzyon, gelecekte enerji krizine çözüm olabilecek büyük bir umut taşır. Bu yöntem, fosil yakıtların çevresel sorunlarını taşımadan ve klasik nükleer enerjinin radyasyon risklerinin çok altında kalarak, muazzam miktarda enerji üretebilir. Temel fikir basittir: Hidrojen gibi hafif elementler aşırı sıcaklık ve basınç altında plazmaya dönüşür; bu parçacıklar çarpışır, birleşir ve enerji açığa çıkar.
Ancak burada ciddi bir mühendislik sorunu ortaya çıkar. Güneşin çekirdeğinden bile daha sıcak bir plazma nasıl tutulur? Hiçbir malzeme bu sıcaklığa dayanamaz. Bu yüzden bilim insanları plazmanın manyetik özelliklerinden faydalanarak onu manyetik alanlarla “havada” tutmaya çalışır.
Fakat topoloji burada devreye girer. Doğal kaplar—kutular, silindirler, küreler—topolojik olarak küredir. Bu şekillerin çevresine yerleştirilen manyetik alanlar, saçlı top teoreminin öngördüğü gibi, bir yerde sıfıra düşer. Bu, manyetik hapsin başarısız olması ve plazmanın sızması anlamına gelir ki bu da felaket demektir.
Sonuç Olarak

Bu yüzden füzyon reaktörleri simit şekline sahiptir. “Tokamak” adı verilen bu tasarım, saçlı top teoremini alt eder. ITER projesi, Fransa’da bu yapının en büyük ve en gelişmiş manyetik sistemini kurmak üzere 2025’e kadar inşaatını tamamlamayı planlıyor. Bu da gösteriyor ki topoloji, yalnızca teorik bir merak değil; geleceğin temiz enerjisinin merkezinde yer alacak kadar gerçek ve etkili bir araç.
Kaynaklar ve ileri okumalar:
- The Hairy Ball Theorem; yayınlanma tarihi: 27 Kasım 2011; Bağlantı: https://www.youtube.com/
- Hairy balls, cyclones and computer graphics; Yayınlanma tarihi: 2 Eylül 2016; Bağlantı: https://chalkdustmagazine.com/
- McGrath, Peter. (2016). An Extremely Short Proof of the Hairy Ball Theorem. The American Mathematical Monthly. 123. 502. 10.4169/amer.math.monthly.123.5.502./
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






