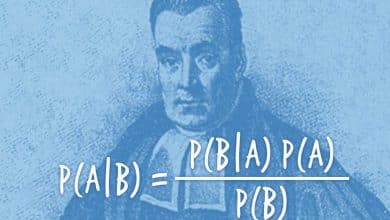Matematiğin “en iyi seçim problemi”, işe alımdan romantik ilişkilere kadar birçok alanda insanların daha sağlıklı kararlar vermesine yardımcı olacaktır.

Otoyolda ilerlerken yakıtınızın azaldığını fark ediyorsunuz. GPS, güzergâh üzerinde 10 benzin istasyonu gösteriyor. Doğal olarak, en ucuz olanı tercih etmek istersiniz. Bunun için uygulanabilecek yöntemlerden biri, ilk birkaç istasyonu geçerken fiyatlarını gözlemlemek ve ardından makul görünen birine girmektir.
Peki ya bir sonraki istasyon daha uygun fiyatlıysa? Gerçekten şimdi mi durmalısınız? Hangi strateji, en ucuz istasyonu seçme ihtimalinizi en çok artırır? Bu sorular bizi “en iyi seçim problemi” olarak bilinen matematiksel bir probleme götürür.
En İyi Seçim Problemi Nedir?
Araştırmacılar, “en iyi seçimi yapma problemi”ni ve çeşitli türlerini uzun süredir inceliyor. Konunun, gerçek hayattaki karşılıkları ve şaşırtıcı derecede sade çözümü, bilim insanlarının ilgisini çekmeye devam ediyor. Gözleme dayalı çalışmalar ise, insanların bu tür durumlarda en etkili stratejiyi çoğu zaman uygulayamadığını gösteriyor.
“En iyi seçim problemi”, farklı isimlerle de anılıyor. Örneğin, “sekreter problemi”, adayların niteliklerine göre sıralandığı iş başvurularını ele alır. “Evlilik problemi” ise, adayların uygunluk derecelerine göre sıralandığı bir başka versiyonudur.
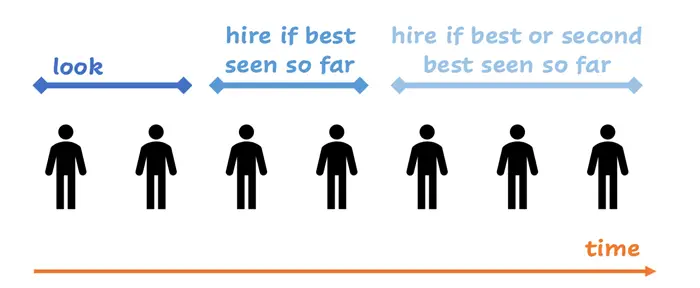
Tüm bu örnekler aynı temel matematiksel yapıyı paylaşır: Sıralanabilir nitelikteki seçenekler, önceden bilinen sayıda ve rastgele sırayla karşınıza çıkar. Her biri için anında karar vermeniz gerekir. Ya kabul edersiniz ya da reddedersiniz — geri dönüş yoktur. Eğer başlangıçta tümünü reddederseniz, sonunda kalan son seçeneği kabul etmek zorunda kalırsınız.
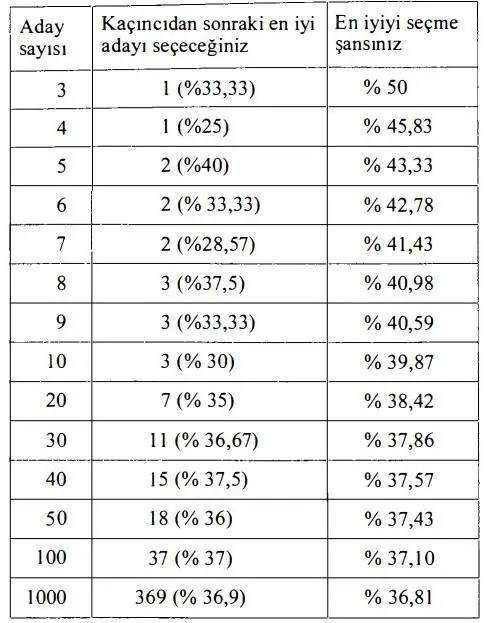
Şimdi baştaki soruya dönelim. Diyelim ki otoyol boyunca 1.000 benzin istasyonu var ve her birini sırayla değerlendirip bir noktada durma kararı vermeniz gerekiyor. Rastgele seçim yaparsanız, en iyi istasyonu bulma ihtimaliniz yalnızca %0,1 olacaktır.
Daha akıllıca bir strateji izleseniz bile, en iyi seçenek çok erken ya da çok geç çıkarsa onu kaçırma riskiniz devam eder. İlginç olan şu ki, en iyi strateji uygulandığında en iyi seçeneğe ulaşma ihtimali yaklaşık %37’ye çıkar. Üstelik bu başarı oranı, toplam aday sayısından bağımsızdır. Bir milyar seçenek bile olsa, yalnızca en iyiyi hedeflediğinizde başarı şansınız yaklaşık üçte birdir.
Yüzde 37 Kuralı Nedir?
Kazandıran strateji şaşırtıcı derecede basittir: İlk yaklaşık %37’lik kısmı, ne olursa olsun reddedin. Ardından, şimdiye kadar gördüklerinizden daha iyi olan ilk seçeneği kabul edin. Eğer böyle bir seçenek çıkmazsa, sonuncusunu seçmek zorunda kalırsınız.
Matematikçilerin favori sabitlerinden biri olan e = 2,718…, bu problemde de karşımıza çıkar. Euler sayısı olarak bilinen e, birçok farklı matematiksel bağlamda beklenmedik şekilde ortaya çıkar. “En iyi seçim problemi”nde de bu sayı gizli bir rol oynar. Stratejide geçen %37 oranı ve başarı ihtimali aslında 1/e, yani yaklaşık %36,8’dir.
Bu oran, iki zıt eğilimin dengesinden doğar: Yeterince örnek görerek bilgi edinmek istersiniz, fakat çok beklerseniz en iyiyi kaçırma riskiniz artar. Matematiksel kanıt, bu gerilimi 1/e oranında gözlem yaparak dengelemenin en iyi sonucu verdiğini gösterir.
Bu problemin yazılı olarak ilk kez yer alması, Martin Gardner’ın Scientific American dergisindeki ünlü Mathematical Games köşesinde gerçekleşti. Günümüzde bu problem, Google Scholar’da binlerce akademik sonuç veriyor ve matematikçiler hâlâ çeşitli varyantlarını araştırmaya devam ediyor:
- Ya birden fazla seçeneği kabul etme hakkınız olsa ve içlerinden biri en iyisi çıksa?
- Ya seçeneklerin sırasını, sizi yanıltmak isteyen biri belirlese?
- Ya da tam olarak en iyisini değil de, ikinci ya da üçüncü en iyiyi kabul etmeye razı olsanız?
Bu tür “ne zaman durmalı?” soruları, optimal durdurma teorisi olarak bilinen matematik dalı tarafından incelenir.
En İyi Seçimi Yapmak Mümkün mü?
Matematikçi David Wees, bu stratejiyi kişisel hayatında uyguladı. Rekabetin yüksek olduğu bir piyasada daire ararken, daireyi başka biri kapmadan önce anında karar vermesi gerektiğini fark etti. Görüşme temposuna ve altı aylık süresine göre, toplamda 26 daire gezebileceğini hesapladı.
Sonrasında 26 dairenin %37’si yaklaşık 10 olduğu için ilk 10 daireyi otomatik olarak eledi. Ardından, o ana kadar gördüğü dairelerden daha iyi olan ilk seçeneği kiralamaya karar verdi. Geriye kalan daireleri hiç görmediği için en iyisini bulup bulmadığını asla bilemeyecekti. Ancak en iyi şansı elde ettiğini bilmek, içini rahatlattı.
Carnegie Mellon Üniversitesi Katar Dekanı Michael Trick, 20’li yaşlarında benzer bir stratejiyi aşk hayatına uyarlamaya çalıştı. İnsanların genellikle 18 yaşında flört etmeye başladığını ve 40 yaşından sonra artık partner aramayacağını varsaydı. Bu sürenin %37’si, 26 yaşına denk geliyordu.
Trick, bu yaştan itibaren daha önce tanıştığı herkesten daha çok beğendiği ilk kadına evlenme teklif etmeye karar verdi. Ms. Right’la tanıştı, diz çöktü ve reddedildi!
Unutmayalım: En iyi seçim problemi, fırsatların sizi reddedebileceği durumları kapsamaz. Belki de romantik ilişkilerde matematiğe güvenmemek daha iyidir.
Sonuç Olarak
Gözleme dayalı araştırmalar, insanların çoğunlukla arayışlarını gereğinden erken sonlandırdığını ortaya koyuyor. Bu nedenle, %37 kuralını uygularsanız, kararlarınızı daha sağlıklı hale getirebilirsiniz. Ancak, yöntemin işe yaraması için bazı koşulların sağlanması gerekir:
- Öncelikle seçenekler, sıralanabilir olmalıdır.
- Tüm seçeneklerin toplam sayısını baştan bilmelisiniz.
- Seçenekler, size rastgele sırayla ve tek tek sunulmalıdır.
Eğer kararlarınızı anında vermek zorunda değilseniz, bu stratejiye ihtiyaç kalmaz. Tüm adayları değerlendirebilir ve en çok beğendiğinizi seçebilirsiniz. Öte yandan, hedefiniz yalnızca en iyiyi değil de genel olarak iyi bir sonucu yakalamaksa, benzer bir strateji hâlâ işinize yarayabilir. Ancak bu durumda, en uygun eşik genellikle %37’den daha düşük olur.
Sonuç olarak, hiçbir strateji size kesin en iyi kararı garanti edemez. Yine de, en iyi seçeneğe ulaşma olasılığınızı en üst düzeye çıkarmanın yolu, sağlam matematiksel temellere dayanır.
Kaynaklar ve ileri okumalar
- Strategic dating: The 37% rule; Yayınlanma tarihi: 1 Mart 2017; Bağlantı: https://plus.maths.org/
- Rapoport, A. (1997). Sequential Decision Making with Relative Ranks: An Experimental Investigation of the “Secretary Problem”>. Organizational Behavior and Human Decision Processes. https://doi.org/10.1006/OBHD.1997.2683
- Murtagh J. Elegant Math Problem Finds the Best Choices. Math’s “best-choice problem” could help people make better decisions. Sci Am. 2025 Jan 1;332(1):76. doi: 10.1038/scientificamerican012025-3zM2h9YmRVcmADeZtd0Ih8. PMID: 39688995.
- Addicott MA, Pearson JM, Sweitzer MM, Barack DL, Platt ML. A Primer on Foraging and the Explore/Exploit Trade-Off for Psychiatry Research. Neuropsychopharmacology. 2017 Sep;42(10):1931-1939. doi: 10.1038/npp.2017.108. Epub 2017 May 29. PMID: 28553839; PMCID: PMC5561336.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel