Herhangi bir haritayı iki rengin birbirine değmeyeceği şekilde boyamak için kullanabileceğiniz en az renk sayısı nedir? Bu soru ilk bakışta oldukça önemsiz bir soru gibi görünecektir. Ancak bu sorunun matematik için inanılmaz derecede önemli teorik ve pratik sonuçları olmuştur. Bu yazıda öncelikle dört renk teoremine sonrasında da sonuçlarına bakacağız.

Dört Renk Teoremi İle Nasıl Tanıştık?
Matematik tarihinin en dikkat çekici olaylarından biri 23 Ekim 1852’de başladı. Augustus De Morgan o gün Sir William Rowan Hamilton’a bir mektup yazdı. Mektubunda sorduğu soru daha sonra matematikçileri hem büyüledi hem de zorladı.
Öğrenci Frederick Guthrie’ydi. Sorduğu fikir aslında kardeşi Francis’in gözleminden geliyordu. Soru Francis’in aklına, Britanya kontluklarının yer aldığı bir haritaya bakarken gelmişti. Soru şu biçimdeydi. Acaba komşu bölgeler farklı renklerde olmak şartıyla her harita en fazla dört renkle boyanabilir mi?
Bu düşünce doğru gibi görünüyordu. De Morgan da bunu sezmişti. Yine de Hamilton bu soruya ilgi duymadı. De Morgan’ın başka matematikçileri konuya çekme çabaları da sonuçsuz kaldı.
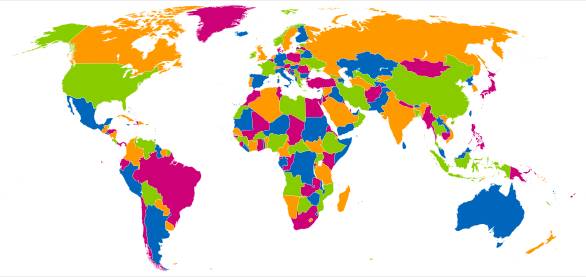
Sorun uzun süre ilgi görmedi ve 1878’e kadar neredeyse unutuldu. O yıl Arthur Cayley, Londra Matematik Derneği üyelerine bu problemin bir kanıtını bulan olup olmadığını sordu. Bu çağrıdan kısa süre sonra çeşitli kanıtlar ortaya çıkmaya başladı. En önemlisi, 1879’da avukat Alfred Kempe tarafından sunulan ilk kanıttı.
Ne yazık ki Kempe’nin kanıtı, sonrasında bir yüzyıl boyunca önerilecek tüm kanıtlar gibi, hatalıydı. Yine de zekice tasarlanmıştı ve nihai kanıtta kullanılacak bazı temel fikirleri içeriyordu.

Dört Renk Teoreminin Çözümü Matematik Camiasını Karıştıracaktı
Bir yüzyıldan uzun süre boyunca birçok matematikçi dört renk teoremini kanıtlamaya çalıştı ama başarılı olamadı. 1976’da Kenneth Appel ve Wolfgang Haken sonunda bunu başardı.
1970’lerin ortasında matematikçiler problemi oldukça sadeleştirmişti. Yine de tek tek incelenmesi gereken 1.936 farklı harita yerleşimi kalmıştı. Bazıları ise gerçekten çok karışıktı. Kenneth Appel ve Wolfgang Haken bu yüzden bilgisayar kullandı. Bilgisayar, her yerleşimi tek tek kontrol etti ve dördüncü renkten fazlasına ihtiyaç olmadığını doğruladı. Bu işlem 1.200 saatlik bilgisayar zamanı gerektirdi.

Dört renk teoremi, bilgisayar kullanılarak kanıtlanan ilk büyük matematik teoremidir. Tarihte ilk kez matematikçiler elle denetlenemeyen büyük bir teoremi kabul etmek zorunda kaldı.
Dört renkten fazlasına ihtiyaç duyan hiçbir harita olmadığını göstermek için Appel ve Haken, matematikçilerin en güçlü yöntemine başvurdu: reductio ad absurdum (olmayana ergi). Yöntemin işleyişi nettir.
Bir önermenin doğru olduğunu göstermek istediğimizde, önce onun yanlış olduğunu varsayarız. Sonra bu varsayımın matematiğin bilinen doğrularıyla çeliştiğini ortaya koyarız. Yani yanlışlık varsayımı kabul edildiğinde matematik “bozulur”. Bu çelişki, önermenin aslında doğru olduğunu kanıtlar.
Bu yöntem bize şunu gösterir: Başlangıçtaki varsayım yanlışsa, kanıtlamaya çalıştığımız ifade doğru olmalıdır. Appel ve Haken bu fikri şöyle uyguladı. Önce tersini varsaydılar; yani dört renkten fazlasına ihtiyaç duyan bir haritanın bir yerlerde var olduğunu kabul ettiler. Sonra bu “istenmeyen” haritanın, 1.936 özel ve daha küçük haritadan hiçbirini içeremeyeceğini gösterdiler.
Ardından ikinci adımı attılar. Her haritanın mutlaka bu 1.936 özel küçük haritadan en az birini içermesi gerektiğini kanıtladılar. Böylece iki sonuç birbiriyle çelişti ve teorem ortaya çıktı. Bu kanıtta çok sayıda kontrol yapılması gerekiyordu. Bu nedenle Appel ve Haken işlemlerin büyük bölümünü gerçekleştirmek için bir bilgisayar programı yazdı.
Ancak kanıtta en büyük rolü bilgisayar üstleniyodu. Bu yüzden teoremin doğruluğu konusunda kaygılar ortaya çıktı; çünkü kanıtı elle doğrulamak neredeyse imkânsızdı. Doğal olarak pek çok kişi kuşkuyla yaklaştı.
Sonuç Olarak
1975’te Amerikalı matematik yazarı Martin Gardner, 1 Nisan şakası olarak dört renk teoremine bir karşı örnek sunduğunu duyurdu. Yalnızca dört rengin yeterli olduğunu göstermek ise 24 yıl sürdü ve ciddi miktarda bilgisayar hesabı gerektirdi.
Bugüne kadar dört renk problemini bilgisayar kullanmadan kanıtlayabilen çıkmadı. Matematik dünyası dört renk problemi için hala daha kısa ve geleneksel yapıda bir matematikçinin ispatını bekliyor. Bugün teorem akademide kabul görse de yine de hâlâ dört renk teoreminden şüphe duyanlar var.
Kaynaklar ve ileri okumalar:
- The Colorful Problem That Has Long Frustrated Mathematicians. Yayınlanma tarihi: 29 Mart 2023. Kaynak site: Quantamagazine. Bağlantı: The Colorful Problem That Has Long Frustrated Mathematicians
- Putting maths on the map with the four colour theorem. Kaynak site: Conversation. Yayınlanma tarihi: 19 Ağustos 2013. Bağlantı: https://doi.org/10.64628/AA.ha4xdquw3
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





